2. MATRICES E DETERMINANTES
Definición de matriz
Chámase matriz de dimensión mxn a unha táboa rectangular
formada por m filas e n columnas de números reais:
aij representa o elemento que está na fila i e na columna j
o elemento a25 será o elemento da fila 2 e columna 5.
3. TIPOS DE MATRICES
Matriz fila: ( )naaaa 1131211
Matriz columna:
1
31
21
11
ma
a
a
a
Matriz nula
Matriz cadrada:
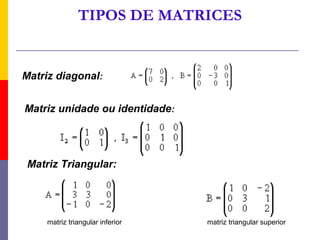
4. TIPOS DE MATRICES
Matriz diagonal:
Matriz unidade ou identidade:
Matriz Triangular:
matriz triangular inferior matriz triangular superior
5. MATRIZ TRASPOSTA
Chámase TRASPOSTA dunha matriz A, a matriz que se
obtén ao cambiar na matriz A as filas polas columnas
Matriz simétrica: Unha matriz cadrada A é simétrica cando A = At
Matriz antisimétrica: Unha matriz cadrada é antisimétrica cando -A = At
6. SUMA E DIFERENCIA DE
MATRICES
non se poden sumar.
A + (B + C) = (A + B) + C Propiedade Asociativa
A + B = B + A Propiedade conmutativa
Matriz NulaA + 0 = A (0 é a matriz nula)
Só se poden sumar ou restar matrices coa mesma dimensión
7. PRODUCTO DUNHA MATRIZ POR UN
NÚMERO
PROPIEDADES PRODUCTO DUN Nº POR UNHA MATRIZ
a.(b.A)=(a.b).A
a.(A+B)=a-A+a.B
(a+b).A=a.A+b.A
1.A=A
8. PROPIEDADES DO PRODUCTO DE MATRICES
Para que dúas matrices se poidan multiplicar é necesario que o nº
de columnas da primeira coincida co nº de filas da segunda
ASOCIATIVA: (A.B).C=A.(B.C).
DISTRIBUTIVA : A.(B+C) = A.B+A.C (A+B).C = A.C+B.C
NON É CONMUTATIVO : A.B ≠ B. A.
PRODUCTO DE MATRICES
9. Unha matriz cadrada que ten inversa dise que é inversible ou
regular; en caso contrario recibe o nome de singular.
MATRIZ INVERSA
Hai varios métodos para calcular a matriz inversa dunha matriz dada:
método de Gauss
Usando determinantes
Directamente
Chámase inversa dunha matriz cadrada A de orden n a outra
matriz de orden n, B que verifique que A·B = B· A = In
Unha matriz cadrada ten inversa cando e só cando o seu
determinante é distinto de 0
10. A matriz que se calculou realmente sería a inversa pola "dereita", pero é fácil
comprobar que tamén cumpre A-1
· A = I, co que é realmente a inversa de A.
Dada a matriz buscamos unha matriz que cumpra A·A-1
= I2, é dicir
Para elo propoñemos o sistema de ecuacións:
Cálculo Directo da Matriz Inversa
11. Cálculo de la Matriz Inversa por
el método de Gauss - Jordan
2º.- Triangularizamos a matriz A de arriba a abaixo e realizamos as mesmas operacións na matriz da dereita
Queremos calcular a inversa de
1º.- Escribese a matriz A seguida da matriz identidade,
Como podemos observar o rango da matriz A é máximo (neste caso 3), polo tanto a matriz A ten inversa,
ímola calcular
3º.- Triangularizamos a matriz de abaixo a arriba, realizando as mesmas operacións na matriz da dereita
4º.- Por último divídese cada fila polo elemento diagonal correspondiente.
12. As dúas primeiras filas son L.I. a terceira depende linealmente das
dúas primeiras
RANGO DUNHA MATRIZ
Vectores fila dunha matriz:
As filas dunha matriz poden ser consideradas como vectores. É posible que
sexan linealmente Independentes (L.I.) e é posible que uns dependan
linealmente de outros. Por exemplo:
As dúas primeiras líñas son L.I., as outras dúas dependen
linealmente das primeiras
As súas dúas son linealmente independentes
=
2431
5232
A
=
43
50
12
31
B
−−
=
158
209
351
C
2123 FFF −⋅= 214 FFF +=
312 FFF =−
Chámase rango dunha matriz ao número de filas Linealmente Independentes
13. Teorema
Nunha matriz o número de filas L.I. coincide co número de
columnas L.I.
RANGO DUNHA MATRIZ
Vectores columna dunha matriz:
Tamén as columnas dunha matriz poden ser consideradas como vectores.
Poderíamos definir rango da matriz como o número de columnas linealmente
independentes, pero aparece a dúbida de se esa definición pode contradecir á
anterior.
Rango dunha matriz é o número de filas, ou columnas,
linealmente independentes.
14. O rango dunha matriz podémolo calcular por dous métodos
diferentes:
RANGO DUNHA MATRIZ
Polo método de Gauss
Usando Determinantes
15. Cálculo do rango: método de Gauss
Se se permutan dúas filas o rango non
varía
Se se multiplica unha fila por un nº non
nulo o rango non varía
Se a unha fila se lle suma ou resta outra
paralela o rango non varía
