2. 自己紹介
氏名 : 山根 嵩史
所属 : 広島大学大学院 教育学研究科
教育人間科学専攻 学習心理学研究室 (D2)
研究テーマ : メタ記憶,読解方略
Mail : t.yamane1969@gmail.com
Twitter : @T_Yamane
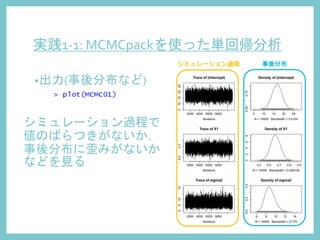
6. 実践1-1: MCMCpackを使った単回帰分析
?MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
formula: 回帰モデル, data: データの指定
burnin: バーンイン期間, mcmc: 繰り返し回数
7. 実践1-1: MCMCpackを使った単回帰分析
?MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
thin: 推定に用いる値のサンプリング間隔
verbose: 途中経過を表示するタイミング
seed: シード値の設定
8. 実践1-1: MCMCpackを使った単回帰分析
?MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
b0: 事前分布の平均, B0: 事前分布の分散
c0: 逆ガンマ分布のshapeパラメータ
d0: 逆ガンマ分布のscaleパラメータ
(その他の引数については参考文献[1]を参照)
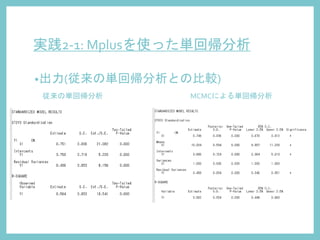
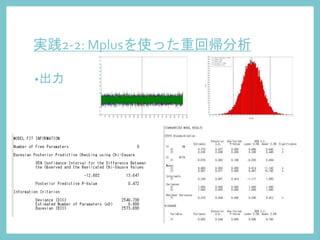
20. 実践2-1: Mplusを使った単回帰分析
?入力 従来の単回帰分析 MCMCによる単回帰分析
ANALYSISコマンドにおいて
“ESTIMATOR = BAYS”でベイズ推定を指定
“POINT = MEDIAN” で推定する値を指定
“CHAIN = 3”でマルコフ連鎖の数を指定
“BITERATIONS = (10000)”でシミュレーション回数を指定
27. Let’s
Bayes!
参考文献
[1]Martin,A. A. D., Quinn, K. M., Park, J. H., Jong, M., & Park, H.
(2013). Package “ MCMCpack ”, (Mcmc).
[2]小杉考司?清水裕士 (編著) (2014). MplusとRによる
構造方程式モデリング入門 北大路書房, pp. 245-261
Editor's Notes ?声量确认 ?当然搁と尘辫濒耻蝉をお使いですよね?








![実践1-1: MCMCpackを使った単回帰分析
?MCMCpackのMCMCregress()関数を使用
MCMCregress(formula, data, burnin = 1000, mcmc = 10000,
thin = 1, verbose = 0, seed = NA, beta.start = NA,
b0 = 0, B0 = 0, c0 = 0.001, d0 = 0.001,
sigma.mu = NA, sigma.var = NA,
marginal.likelihood = c("none", "Laplace", "Chib95"), ...)
b0: 事前分布の平均, B0: 事前分布の分散
c0: 逆ガンマ分布のshapeパラメータ
d0: 逆ガンマ分布のscaleパラメータ
(その他の引数については参考文献[1]を参照)](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-8-320.jpg)












![実践2-1: Mplusを使った単回帰分析
?出力(シミュレーション過程と事後分布)
出力画面で[plot]→[view plot]からチェック
シミュレーション過程
(Bayesian posterior parameter trace plots)
事後分布
(Bayesian posterior parameter distributions)](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-22-320.jpg)


![Let’s
Bayes!
参考文献
[1]Martin,A. A. D., Quinn, K. M., Park, J. H., Jong, M., & Park, H.
(2013). Package “ MCMCpack ”, (Mcmc).
[2]小杉考司?清水裕士 (編著) (2014). MplusとRによる
構造方程式モデリング入門 北大路書房, pp. 245-261](https://image.slidesharecdn.com/mcmc-140609001607-phpapp01/85/MCMC-27-320.jpg)