Measurement Theory.ppt
- 1. Theory of Errors in Observations
- 2. Errors in Measurement ’ü¼ No Measurement is Exact ’ü¼ Every Measurement Contains Errors ’ü¼ The ŌĆ£TrueŌĆØ Value of a Measurement is Never Known ’ü¼ The ŌĆ£ExactŌĆØ Error Present is Always Unknown
- 3. Mistakes or Blunders ’ü¼ Caused by: ŌĆō Carelessness ŌĆō Poor Judgement ŌĆō Incompetence
- 4. Sources of Errors ’ü¼ Natural ŌĆō Environmental conditions: wind, temperature, humidity etc. ŌĆō Tape contracts and expands due to temperature changes ŌĆō Difficult to read Philadelphia Rod with heat waves coming up from the pavement
- 5. Sources of Errors ’ü¼ Instrumental ŌĆō Due to Limitation of Equipment ’ü¼ Warped Philadelphia Rod ’ü¼ Theodolite out of adjustment ’ü¼ Kinked or damaged Tape
- 6. Sources of Errors ’ü¼ Personal ŌĆō Limits of Human Performance Factors ’ü¼ Sight ’ü¼ Strength ’ü¼ Judgement ’ü¼ Communication
- 7. Types of Errors ’ü¼ Systematic/Cumulative ŌĆō Errors that occur each time a measurement is made ŌĆō These Errors can be eliminated by making corrections to your measurements ’ü¼ Tape is too long or to short ’ü¼ Theodolite is out of adjustment ’ü¼ Warped Philadelphia Rod
- 8. Precision vs. Accuracy ’ü¼ Precision ŌĆō The ŌĆ£ClosenessŌĆØ of one measurement to another
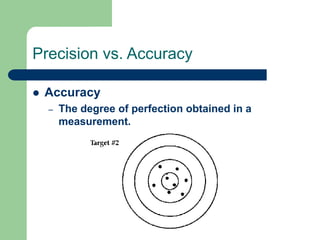
- 9. Precision vs. Accuracy ’ü¼ Accuracy ŌĆō The degree of perfection obtained in a measurement.
- 10. Precision and Accuracy ’ü¼ Ultimate Goal of the Surveyor ŌĆō Rarely Obtainable ŌĆō Surveyor is happy with Precise Measurements
- 12. Probability ’ü¼ Surveying measurements tend to follow a normal distribution or ŌĆ£bellŌĆØ curve ŌĆō Observations ’ü¼ Small errors occur more frequently than larger ones ’ü¼ Positive and negative errors of the same magnitude occur with equal frequency ’ü¼ Large errors are probably mistakes
- 13. Most Probable Value (MPV) Also known as the arithmetic mean or average value MPV = ’āźM n The MPV is the sum of all of the measurements divided by the total number of measurements
- 14. Standard Deviation (’ü│) Also known as the Standard Error or Variance ’ü│2 = ’āź(M-MPV) n-1 M-MPV is referred to as the Residual ’ü│ is computed by taking the square root of the above equation
- 15. Example: A distance is measured repeatedly in the field and the following measurements are recorded: 31.459 m, 31.458 m, 31.460 m, 31.854 m and 31.457 m. Compute the most probable value (MPV), standard error and standard error of the mean for the data. Explain the significance of each computed value as it relates to statistical theory.
- 16. Solution: Measurement M - Mbar (M-Mbar)2 31.459 0 0 31.458 -0.0010 0.0000010 31.460 0.0010 0.0000010 31.457 -0.0020 0.0000040 Sum = 125.834 0.0000060 MPV or Mbar= 125.834 / 4 = 31.459 m
- 17. Solution (continued): S.E. = +/- ((0.0000060)/(4-1))1/2 = +/- 0.0014 m Say +/- 0.001 m Em = 0.001/(4)1/2 = +/- 0.0005 m Say +/- 0.001 m
- 18. Explanation: The MPV is 31.459 m. The value that is most likely to occur. This value represents the peak value on the normal distribution curve. The standard error is +/- 0.001 m . 68.27% of the values would be expected to lie between the values of 31.458 m and 31.460 m. These values were computed using the MPV+/- the standard error.
- 19. Explanation (continued): The standard error of the mean is +/- 0.001 m . The ŌĆ£trueŌĆØ length has a 68.27% chance of being within the values of 31.458m and 31.460 m. These values were computed using the MPV +/- Em.