Meccanicadei sistemi
- 1. Meccanica dei Sistemi Corso di Fisica - UdA 1
- 2. Principio di Conservazione della Quantità di Moto Supponiamo che su un corpo agisca dall’esterno un insieme di forze tali che la loro risultante sia nulla. In tal caso avremo che: ΣF = 0 = Δp/Δt Δp = 0 Se Δp = 0 ne consegue che p = costante. Possiamo quindi enunciare il Principio di Conservazione della Quantità di Moto: Se la risultante delle forze esterne agenti su un corpo è nulla la quantità di moto totale del corpo si conserva Corso di Fisica - UdA 2
- 3. Urti Nel caso di un urto tra due palline da biliardo, la risultante delle forze esterne (forza peso e reazione vincolare) è nulla, per cui possiamo scrivere: m1v1 + m2v2 = m1v1’ + m2v2’ Questo problema non può essere risolto con la sola equazione suscritta perché le velocità incognite dopo l’urto sono due. Corso di Fisica - UdA 3
- 4. Urti elastici e conservazione dell’energia cinetica Se i due corpi sono molto rigidi, come appunto le due palline da biliardo, e non viene prodotto calore durante l’urto, anche l’energia cinetica totale si conserva. Un tale tipo di urto si dice urto elastico. Allora potremo scrivere una seconda equazione: ½ m1v12 + ½ m2v22 = ½ m1v1’2 + ½ m2v2’2 Che messa a sistema con la precedente ci permette di risolvere il problema. Nel caso in cui l’energia cinetica non si conserva l’urto è detto anelastico. In questo caso l’energia totale si conserverà sempre ma quella cinetica si trasforma in altra forma di energia (ad es. calore) Corso di Fisica - UdA 4
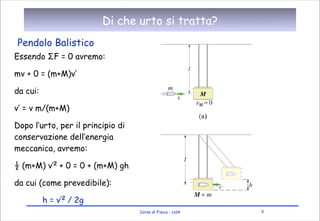
- 5. Di che urto si tratta? Pendolo Balistico Essendo ΣF = 0 avremo: mv + 0 = (m+M)v’ da cui: v’ = v m/(m+M) Dopo l’urto, per il principio di conservazione dell’energia meccanica, avremo: ½ (m+M) v’2 + 0 = 0 + (m+M) gh da cui (come prevedibile): h = v’2 / 2g Corso di Fisica - UdA 5
- 6. Di che urto si tratta? Corso di Fisica - UdA 6
- 7. Centro di Massa Corso di Fisica - UdA 7
- 8. Centro di Massa I corpi estesi sono soggetti a moti più complessi di quelli delle singole particelle, e in genere sono composizioni di traslazioni e rotazioni. Tuttavia, anche se un corpo esteso ruota o se parti del corpo esteso ruotano una rispetto alle altre, in generale esiste un punto che si muove lungo lo stesso percorso in cui si muoverebbe una particella se soggetta alla stessa forza risultante a cui è soggetto l’intero sistema. Tale punto si chiama Centro di Massa (CM), o Centro di Gravità , o Baricentro del corpo. Come vedremo più avanti il moto totale di un corpo esteso può essere considerato come la somma di un moto traslatorio del centro di massa più un moto rotatorio, anche istantaneo, attorno ad esso. Corso di Fisica - UdA 8
- 9. Moto del Centro di Massa Corso di Fisica - UdA 9
- 10. Posizione del Centro di Massa La posizione del CM può essere trovata pensando che in esso si applica la risultante di tutte le forze peso elementari che agiscono su ogni elemento di massa Δm che costituisce il corpo esteso. La posizione del CM è intuibile nei solidi geometrici, ma può capitare ovunque in corpi CM estesi di forma qualsiasi (anche fuori dal corpo!) Mg CM CM Mg Mg Corso di Fisica - UdA 10
- 11. Centro di Massa Corso di Fisica - UdA 11
- 12. Posizione del Centro di Massa Nel caso di due palline tra loro vincolate, la posizione del CM si trova in un punto intermedio tra m1 ed m2 di coordinata: xCM = (m1x1 + m2x2)/(m1+m2) = (m1x1 + m2x2)/M e se le masse sono uguali ovviamente xCM cade nel punto di mezzo: xCM = m(x1 +x2)/2m = (x1 + x2)/2 Corso di Fisica - UdA 12
- 13. Come trovare il Baricentro Corso di Fisica - UdA 13
- 14. Corpi rigidi Si definisce corpo rigido un corpo che, soggetto a forze esterne di qualsiasi intensità , non si deforma . L’applicazione di una forza esterna ad un corpo rigido può provocarne la traslazione e/o la rotazione rispetto ad un punto O qualsiasi. Corso di Fisica - UdA 14
- 15. Rotazione di corpi rigidi Non sempre i corpi rigidi ruotano con moto uniforme. Se la velocità angolare ω non è costante dovremo considerare: ω = Δθ/Δt, ovvero la velocità angolare istantanea se Δt è molto piccolo, e: α = Δω/Δt, ovvero l’accelerazione angolare istantanea, sempre con la stessa ipotesi. In questo caso si manifesta una componente tangenziale dell’accelerazione a (che quindi non sarà più solo centripeta). Corso di Fisica - UdA 15
- 16. Causa della rotazione di corpi rigidi Applicando una forza ad un corpo vincolato ad un asse (ad es. una porta) ci rendiamo conto che la rotazione che otteniamo dipende dall’orientamento della forza e dalla distanza del suo punto di applicazione dall’asse di rotazione (braccio), oltre che dall’intensità della forza stessa. Corso di Fisica - UdA 16
- 17. Momento Torcente Si definisce Momento M di una forza – o momento torcente – rispetto al punto O il prodotto vettoriale: Il momento della forza si misura in N m (Newton metri) Corso di Fisica - UdA 17
- 18. Equazioni della Statica Un corpo rigido è in equilibrio se: Equilibrio alla Traslazione Equilibrio alla Rotazione rispetto ad un qualsiasi punto Le due relazioni sopra sono vettoriali e si possono quindi riscrivere proiettando i vettori sugli assi x, y, z. Corso di Fisica - UdA 18
- 19. Leve All’equilibrio, le forze dirette verso il basso sono annullate dalla reazione vincolare nel fulcro. Se si sceglie un asse di rotazione passante per il fulcro, gli unici momenti sono quelli di Fr e Fp, che dovranno avere risultante nullo: Frrsinθ – FpRsinθ = 0 Fr o, più in generale, quando r perp. F: Frrr=Fprp da cui si ricava l’espressione del guadagno meccanico della leva: Fp/Fr = rr/rp Corso di Fisica - UdA 19
- 20. LE LEVE La leva è una macchina semplice caratterizzata da:  forza attiva (Fp, potenza)  forza passiva (Fr, resistenza)  fulcro Le leve si distinguono in leve di:  PRIMO GENERE  SECONDO GENERE  TERZO GENERE Guadagno meccanico : Fp/Fr = rr/rp Corso di Fisica - UdA 20
- 21. SCHEMA E GENERE DELLE LEVE Leva di primo genere Leva di secondo genere Leva di terzo genere Corso di Fisica - UdA 21
- 22. ESEMPIO DI LEVA DEL PRIMO GENERE NEL CORPO  Forza attiva di potenza → sistema dei muscoli splenici e sub-occipitali  Forza passiva → peso del cranio  Fulcro → atlante All’equilibrio, il braccio della resistenza è circa 3-4 volte più grande di quello della forza attiva esercitata dai muscoli per mantenere il capo in stazione eretta. La leva, detta di bilanciamento, è svantaggiosa Corso di Fisica - UdA 22
- 23. ESEMPIO DI LEVA DEL SECONDO GENERE NEL CORPO  Forza attiva di potenza → muscoli gemelli  Forza passiva → scarico del peso del corpo sul piede  Fulcro → metatarso All’equilibrio, il braccio della forza attiva è maggiore di quello della forza passiva: La leva, detta di potenza, è vantaggiosa Corso di Fisica - UdA 23
- 24. ESEMPIO DI LEVA DEL TERZO GENERE NEL CORPO  Forza attiva di potenza → forza espressa dal bicipite e dal tricipite  Forza passiva → peso avambraccio + eventuale carico  Fulcro → articolazione del gomito All’equilibrio, il braccio della forza attiva è minore di quello della forza passiva: La leva è svantaggiosa Corso di Fisica - UdA 24
- 25. Equilibrio stabile, instabile, indifferente • Eq. stabile: il baricentro è sotto il punto di appoggio; • Eq. Instabile: il baricentro è sopra il punto di appoggio; • Eq. Indifferente: il baricentro coincide con il punto di vincolo. (c) Corso di Fisica - UdA 25
- 26. Base di appoggio Il frigorifero ritorna nella sua posizione iniziale soltanto fino a che la retta di applicazione della forza peso cade nella base di appoggio. Corso di Fisica - UdA 26