Mekanika rekayasa gabungan
1 like4,043 views
Sistem gaya pada suatu struktur dalam keadaan keseimbangan jika memenuhi syarat-syarat keseimbangan translasi dan rotasi, yaitu jika resultan gaya-gaya sama dengan nol dan momen gaya-gaya juga sama dengan nol. Keseimbangan dapat dicapai melalui metode poligon gaya tertutup atau dengan menyelesaikan persamaan keseimbangan.
Mekanika rekayasa gabungan
- 1. MEKANIKA REKAYASA llmu Rekayasa Klasik Sebagai Sarana Menguasai Program Aplikasi Rekayasa
- 2. Masih perlukah mempelajari Mekanika Teknik Klasik dalam Era Serba Komputer ?
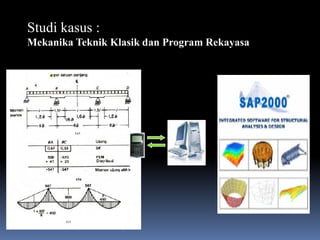
- 3. Studi kasus : Mekanika Teknik Klasik dan Program Rekayasa
- 4. Mekanika Teknik (MT) Mekanika Rekaya Analisa Struktur Structural Analysis ♯ MT Mata kuliah wajib di S1 teknik sipil ♯ Isi MT mayoritas metoda klasik manual ♯ Pemahaman tentang MTsangat membantu profesi bidang rekayasa konstruksi ♯ MT cara manual jarang dipakai di dunia kerja karena digantikan dengan program komputer (kecuali struktur yang sederhana) ♯ MT melatih mahasiswa : memahami perilaku gaya gaya aksi /reaksi pada struktur bangunan
- 5. Program Aplikasi Komputer untuk Rekayasa (Analisa Struktur) Sangat canggih, mudah pengoperasiannya, menu yg user- friendly seperti Windows Relatif mudah didapat, dari yang mahal atau murah bahkan ada yang gratis di internet (di down-load) Andalan insinyur untuk perencanaan struktur yang sebenarnya Perkembangan dunia komputer sangat pesat dan berimbas juga ke dunia rekayasa konstruksi
- 6. Dampak ke profesi engineer? Apakah profesi insinyur (sipil) yang hampir selalu berkecimpung dengan pekerjaan hitung-menghitung juga dapat diganti komputer?
- 7. Hardware semakin murah, software ada kecenderungan ope source (gratis) Apakah jika telah membeli atau mempunyai piranti yang dimaksud maka penyelesaian mekanika teknik secara otomatis dapat diperoleh?
- 38. PEMODELAN STRUKTUR October, 6 2009 Relly Andayani
- 39. Structural Types Continous Beam
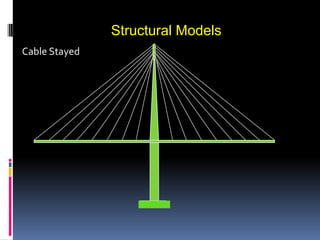
- 40. Structural Types Cable Stayed
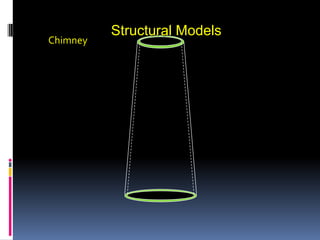
- 41. Structural Types Chimney
- 43. Structural Types Suspension Bridge
- 45. Structural Types Damm
- 49. LOADS
- 50. 堰看敬??? ??? ???????
- 51. Structural Models Continous Beam
- 52. Structural Models Continous Beam
- 53. Structural Models Cable Stayed
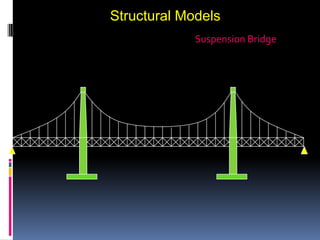
- 59. Structural Models Suspension Bridge
- 60. Structural Models Suspension Bridge
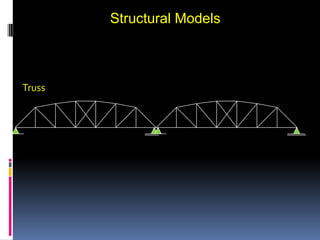
- 65. Structural Models Truss
- 69. LOADS LOADS Spread Load
- 70. LOADS LOADS Spread Load
- 71. LOADS
- 72. LOADS
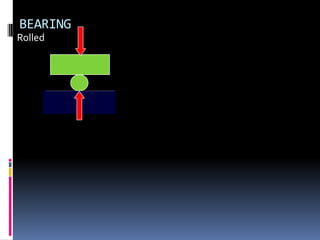
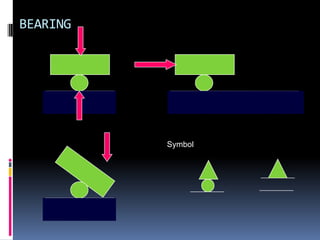
- 73. BEARING Rolled
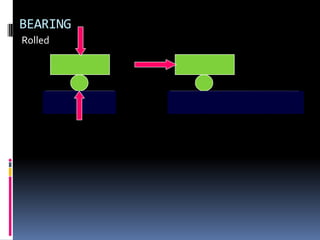
- 74. BEARING Rolled
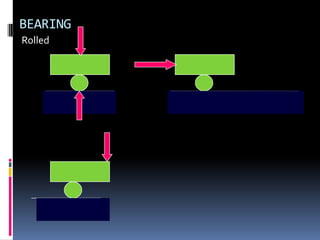
- 75. BEARING Rolled
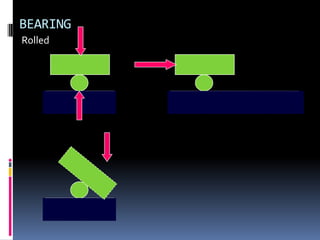
- 76. BEARING Rolled
- 77. BEARING Symbol
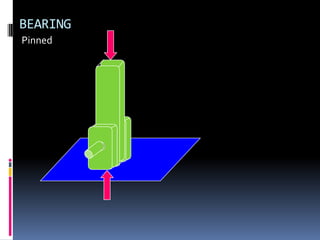
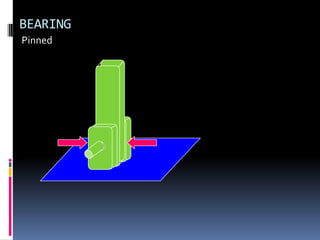
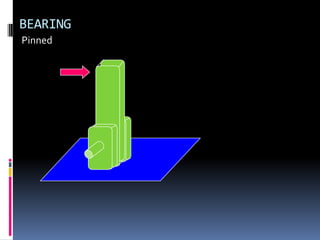
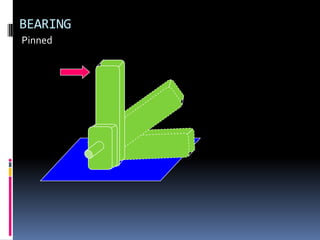
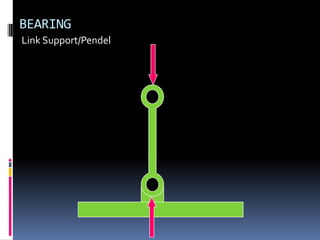
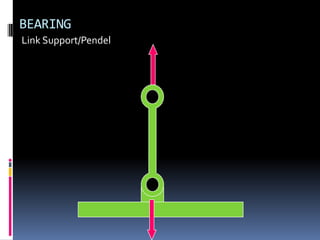
- 78. BEARING Pinned
- 79. BEARING Pinned
- 80. BEARING Pinned
- 81. BEARING Pinned
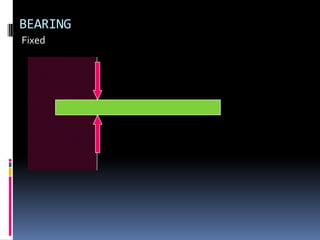
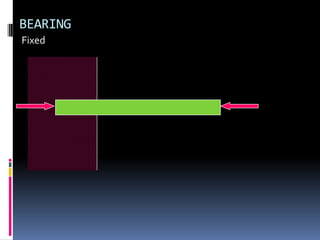
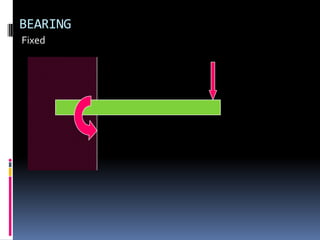
- 82. BEARING Fixed
- 83. BEARING Fixed
- 84. BEARING Fixed
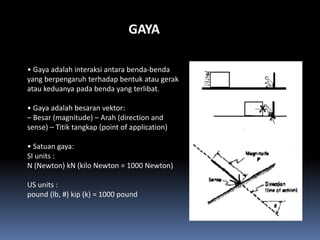
- 89. GAYA Gaya adalah interaksi antara benda-benda yang berpengaruh terhadap bentuk atau gerak atau keduanya pada benda yang terlibat. Gaya adalah besaran vektor: Besar (magnitude) Arah (direction and sense) Titik tangkap (point of application) Satuan gaya: SI units : N (Newton) kN (kilo Newton = 1000 Newton) US units : pound (lb, #) kip (k) = 1000 pound
- 90. Mekanika dan Statika Bagaimana beban mempengaruhi struktur Statika : obyek yang dikenai gaya berada dalam keseimbangan (tidak bergerak, tidak ada percepatan) Gaya-gaya Tumpuan dan hubungan Keseimbangan Mekanika : obyek yang dikenai gaya dapat berubah bentuk Tegangan dan regangan Defleksi Tekuk
- 91. GAYA Presentasi gaya: Secara matematis Secara grafis Secara grafis: sebagai garis : panjang garis besar gaya arah garis arah gaya garis kerja garis yang panjangnya tak tertentu yang terdapat pada vektor gaya tersebut Besar gaya : L Newton, misal jika 1 Newton digambarkan dengan panjang garis 1 cm , maka 4 Newton 4 cm Arah gaya dinyatakan dalam : tg atau besar sudut 留 (属) x y ,
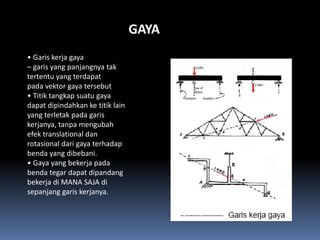
- 92. GAYA Garis kerja gaya garis yang panjangnya tak tertentu yang terdapat pada vektor gaya tersebut Titik tangkap suatu gaya dapat dipindahkan ke titik lain yang terletak pada garis kerjanya, tanpa mengubah efek translational dan rotasional dari gaya terhadap benda yang dibebani. Gaya yang bekerja pada benda tegar dapat dipandang bekerja di MANA SAJA di sepanjang garis kerjanya.
- 93. SISTEM GAYA
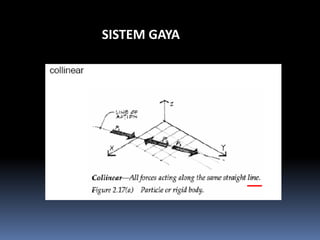
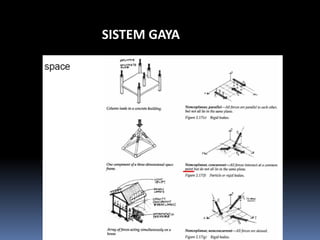
- 94. SISTEM GAYA Macam sistem gaya: collinear coplanar Concurrent Parallel Non-concurrent, non-paralel space Noncoplanar, parallel Noncoplanar, concurrent Noncoplanar, nonconcurrent,
- 95. SISTEM GAYA
- 96. SISTEM GAYA
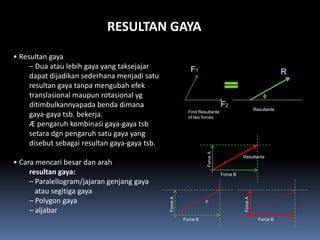
- 97. RESULTAN GAYA Resultan gaya Dua atau lebih gaya yang taksejajar F1 dapat dijadikan sederhana menjadi satu R resultan gaya tanpa mengubah efek translasional maupun rotasional yg ditimbulkannyapada benda dimana F2 Resultante gaya-gaya tsb. bekerja. Find Resultante of two forces pengaruh kombinasi gaya-gaya tsb setara dgn pengaruh satu gaya yang disebut sebagai resultan gaya-gaya tsb. Force A Resultante Cara mencari besar dan arah resultan gaya: Force B Paralellogram/jajaran genjang gaya atau segitiga gaya Polygon gaya Force A Force A F aljabar Force B Force B
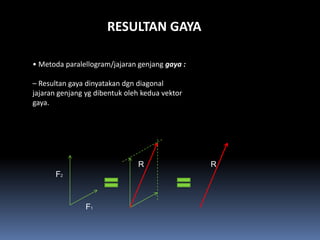
- 98. RESULTAN GAYA Metoda paralellogram/jajaran genjang gaya : Resultan gaya dinyatakan dgn diagonal jajaran genjang yg dibentuk oleh kedua vektor gaya. R R F2 F1
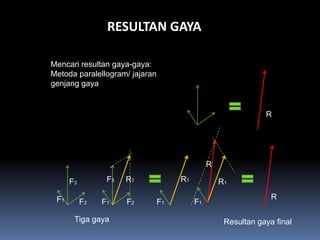
- 99. RESULTAN GAYA Mencari resultan gaya-gaya: Metoda paralellogram/ jajaran genjang gaya R R F3 F3 R1 R1 R1 F1 R F2 F1 F2 F1 F1 Tiga gaya Resultan gaya final
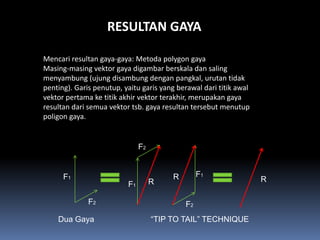
- 100. RESULTAN GAYA Mencari resultan gaya-gaya: Metoda polygon gaya Masing-masing vektor gaya digambar berskala dan saling menyambung (ujung disambung dengan pangkal, urutan tidak penting). Garis penutup, yaitu garis yang berawal dari titik awal vektor pertama ke titik akhir vektor terakhir, merupakan gaya resultan dari semua vektor tsb. gaya resultan tersebut menutup poligon gaya. F2 F1 R F1 R R F1 F2 F2 Dua Gaya TIP TO TAIL TECHNIQUE
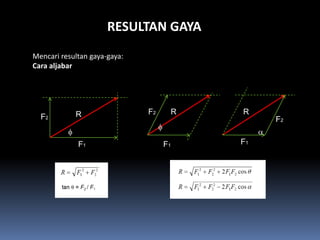
- 101. RESULTAN GAYA Mencari resultan gaya-gaya: Cara aljabar R F2 R R F2 F2 留 F1 F1 F1
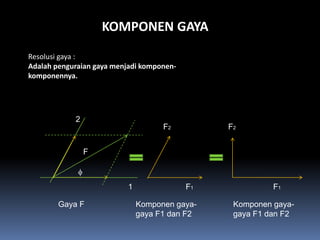
- 102. KOMPONEN GAYA Resolusi gaya : Adalah penguraian gaya menjadi komponen- komponennya. 2 F2 F2 F 1 F1 F1 Gaya F Komponen gaya- Komponen gaya- gaya F1 dan F2 gaya F1 dan F2
- 103. KOMPONEN GAYA Mencari komponen gaya: Cara grafis F1 Force F Force F Force F F1 F1 F2 F2 F2 F1 dan F2 adalah komponen gaya dari gaya F. Sebuah gaya dapat diuraikan menjadi sistem komponen gaya yang berbeda-beda.
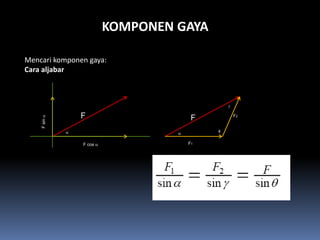
- 104. KOMPONEN GAYA Mencari komponen gaya: Cara aljabar 粒 F F F2 F sin 留 留 留 F cos 留 F1
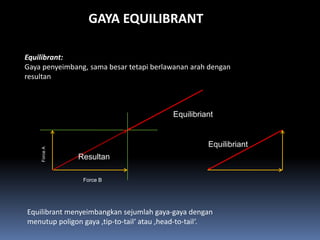
- 105. GAYA EQUILIBRANT Equilibrant: Gaya penyeimbang, sama besar tetapi berlawanan arah dengan resultan Equilibriant Equilibriant Force A Resultan Force B Equilibrant menyeimbangkan sejumlah gaya-gaya dengan menutup poligon gaya tip-to-tail atau head-to-tail.
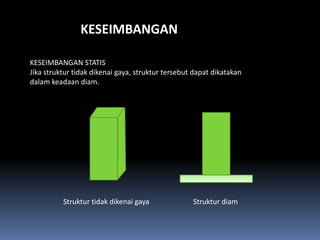
- 106. KESEIMBANGAN KESEIMBANGAN STATIS Jika struktur tidak dikenai gaya, struktur tersebut dapat dikatakan dalam keadaan diam. Struktur tidak dikenai gaya Struktur diam
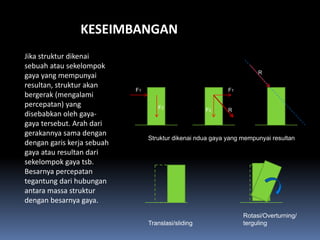
- 107. KESEIMBANGAN Jika struktur dikenai sebuah atau sekelompok gaya yang mempunyai R resultan, struktur akan F1 F1 bergerak (mengalami percepatan) yang F2 F2 R disebabkan oleh gaya- gaya tersebut. Arah dari gerakannya sama dengan Struktur dikenai ndua gaya yang mempunyai resultan dengan garis kerja sebuah gaya atau resultan dari sekelompok gaya tsb. Besarnya percepatan tegantung dari hubungan antara massa struktur dengan besarnya gaya. Rotasi/Overturning/ Translasi/sliding terguling
- 108. KESEIMBANGAN STATIS Jika struktur dikenai sekumpulan gaya yang tidak mempunyai resultan, yaitu sekumpulan gaya yang membentuk segitiga gaya atau poligon gaya yang tertutup, struktur tersebut dapat tetap diam dalam keadaan kesetimbangan statis. F1 F1 F1 F2 F2 R F2 F3 F3 F3 1 2 3 1. Struktur dikenai 3 gaya 2. R adalah resultan dari gaya F1 dan F2, R dan F3 saling meniadakan (F3 adalah equilibriant dari gaya resultan R) 3. F1, F3, dan F3 membentuk segitiga gaya (poligon gaya) tertutup
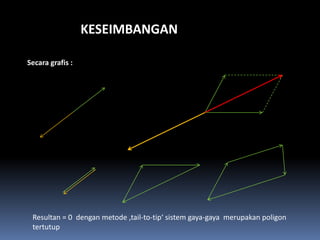
- 109. KESEIMBANGAN Secara grafis : Resultan = 0 dengan metode tail-to-tip sistem gaya-gaya merupakan poligon tertutup
- 110. KESEIMBANGAN KESEIMBANGAN BENDA TEGAR Kondisi keseimbangan: Semua gaya eksternal yang bekerja pada benda tegar membentuk sistem gaya-gaya yang ekuivalen dengan 0 (zero). Tidak terjadi translasi maupun rotasi. Secara analitis: Keseimbangan translasional: Total dari seluruh komponen vertikal seluruh gaya = 0 裡Fv = 0 Total dari seluruh komponen gaya horisontal dari seluruh gaya = 0 裡FH = 0 Keseimbangan rotasional Total dari seluruh momen dari seluruh gaya = 0 裡M = 0
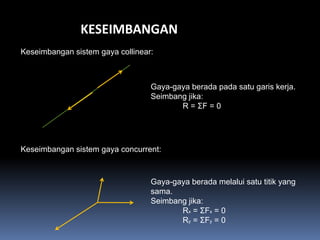
- 111. KESEIMBANGAN Keseimbangan sistem gaya collinear: Gaya-gaya berada pada satu garis kerja. Seimbang jika: R = 裡F = 0 Keseimbangan sistem gaya concurrent: Gaya-gaya berada melalui satu titik yang sama. Seimbang jika: Rx = 裡Fx = 0 Ry = 裡Fy = 0
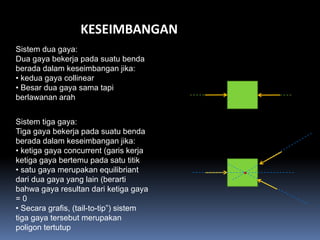
- 112. KESEIMBANGAN Sistem dua gaya: Dua gaya bekerja pada suatu benda berada dalam keseimbangan jika: kedua gaya collinear Besar dua gaya sama tapi berlawanan arah Sistem tiga gaya: Tiga gaya bekerja pada suatu benda berada dalam keseimbangan jika: ketiga gaya concurrent (garis kerja ketiga gaya bertemu pada satu titik satu gaya merupakan equilibriant dari dua gaya yang lain (berarti bahwa gaya resultan dari ketiga gaya =0 Secara grafis, (tail-to-tip) sistem tiga gaya tersebut merupakan poligon tertutup
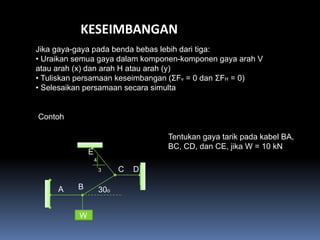
- 113. KESEIMBANGAN Jika gaya-gaya pada benda bebas lebih dari tiga: Uraikan semua gaya dalam komponen-komponen gaya arah V atau arah (x) dan arah H atau arah (y) Tuliskan persamaan keseimbangan (裡Fv = 0 dan 裡FH = 0) Selesaikan persamaan secara simulta Contoh Tentukan gaya tarik pada kabel BA, BC, CD, dan CE, jika W = 10 kN E 4 3 C D A B 30o W
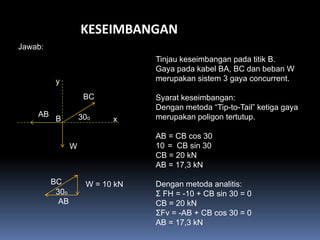
- 114. KESEIMBANGAN Jawab: Tinjau keseimbangan pada titik B. Gaya pada kabel BA, BC dan beban W y merupakan sistem 3 gaya concurrent. BC Syarat keseimbangan: Dengan metoda Tip-to-Tail ketiga gaya AB 30o merupakan poligon tertutup. B x AB = CB cos 30 W 10 = CB sin 30 CB = 20 kN AB = 17,3 kN BC W = 10 kN Dengan metoda analitis: 30o 裡 FH = -10 + CB sin 30 = 0 AB CB = 20 kN 裡Fv = -AB + CB cos 30 = 0 AB = 17,3 kN
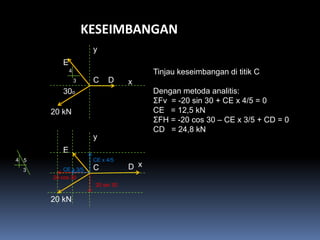
- 115. KESEIMBANGAN y E 4 Tinjau keseimbangan di titik C 3 C D x 30o Dengan metoda analitis: 裡Fv = -20 sin 30 + CE x 4/5 = 0 20 kN CE = 12,5 kN 裡FH = -20 cos 30 CE x 3/5 + CD = 0 CD = 24,8 kN y E 4 5 CE x 4/5 3 CE x 3/5 C D x 20 cos 30 20 sin 30 20 kN
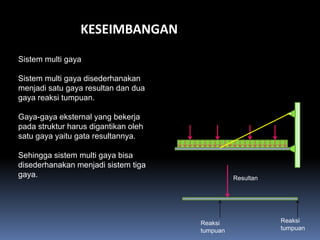
- 116. KESEIMBANGAN Sistem multi gaya Sistem multi gaya disederhanakan menjadi satu gaya resultan dan dua gaya reaksi tumpuan. Gaya-gaya eksternal yang bekerja pada struktur harus digantikan oleh satu gaya yaitu gata resultannya. Sehingga sistem multi gaya bisa disederhanakan menjadi sistem tiga gaya. Resultan Reaksi Reaksi tumpuan tumpuan
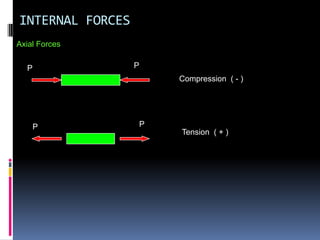
- 117. INTERNAL FORCES Axial Forces P P Compression ( - ) P P Tension ( + )
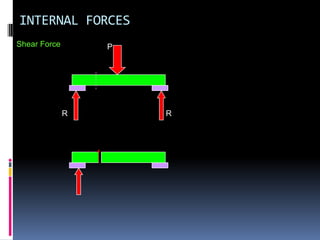
- 118. INTERNAL FORCES Shear Force P R R
- 119. INTERNAL FORCES Moment P +++ RAV RBV
- 120. STRUKTUR RANGKA BATANG Asumsi: Terdiri dari batang-batang struktur yang dihubungkan satu sama lain dengan sendi tanpa ada pergesekan Gaya-gaya bekerja pada titik-titik simpul Gaya yang bekerja pada titik simpul didistribusikan ke anggota rangka batang menurut sumbu batang Jika gaya batang menyebabkan batang bertambah panjang, batang tersebut menahan gaya tarik (positif), dan sebaliknya, jika gaya batang menyebabkan batang bertambah pendek, batang tersebut menahan gaya tekan (negatif) Perubahan panjang akibat gaya yang bekerja diabaikan
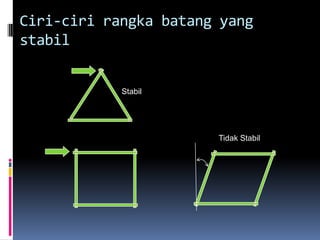
- 121. Ciri-ciri rangka batang yang stabil Stabil Tidak Stabil
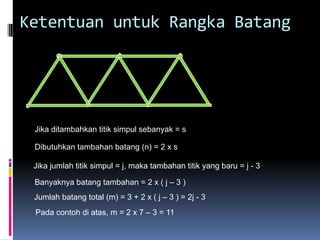
- 122. Ketentuan untuk Rangka Batang Jika ditambahkan titik simpul sebanyak = s Dibutuhkan tambahan batang (n) = 2 x s Jika jumlah titik simpul = j, maka tambahan titik yang baru = j - 3 Banyaknya batang tambahan = 2 x ( j 3 ) Jumlah batang total (m) = 3 + 2 x ( j 3 ) = 2j - 3 Pada contoh di atas, m = 2 x 7 3 = 11
- 123. Cara Perhitungan Rangka Batang Keseimbangan titik simpul {analitis (method of joint) dan grafis (Cremona)} Metode potongan {analitis (Ritter) dan grafis (Culman)}
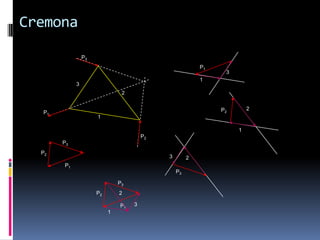
- 124. Cremona P3 P1 3 1 3 2 P2 2 P1 1 1 P2 P3 P2 3 2 P1 P3 P3 P2 2 P1 3 1
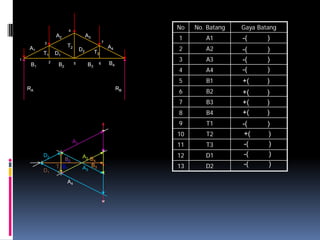
- 125. 4 No No. Batang Gaya Batang A2 A3 7 1 A1 -( ) 3 T2 A1 D2 T3 A4 2 A2 -( ) T1 D1 1 2 3 A3 -( ) B1 B2 5 B3 6 B4 4 A4 -( ) 5 B1 +( ) RA RB 6 B2 +( ) 7 B3 +( ) 8 B4 +( ) 9 T1 -( ) 10 T2 +( ) A1 11 T3 -( ) D2 A2 B 12 D1 -( ) B2 4 T2 B1 A B3 13 D2 -( ) D1 3 A4
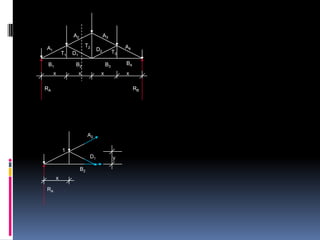
- 126. A2 A3 A1 T2 A4 D2 T3 T1 D1 B1 B2 B3 B4 x x x x RA RB M 1 =0 A2 ( RA x) ( P x) ( B2 y ) = 0 1 D1 y B2 x RA
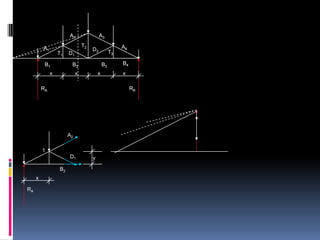
- 127. A2 A3 A1 T2 A4 D2 T3 T1 D1 B1 B2 B3 B4 x x x x RA RB A2 1 D1 y B2 x RA
- 128. FORCES RESULTANTE
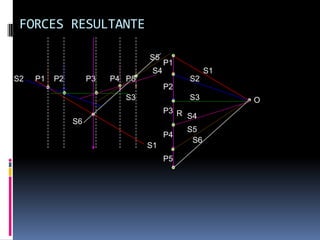
- 129. FORCES RESULTANTE S5 P1 S4 S1 S2 P1 P2 P3 P4 P5 S2 P2 S3 S3 O P3 R S4 S6 S5 P4 S6 S1 P5
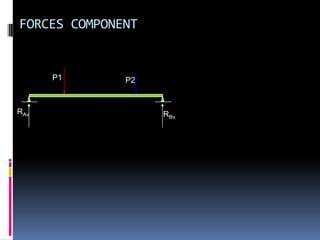
- 130. FORCES COMPONENT P1 P2 RAv RBv
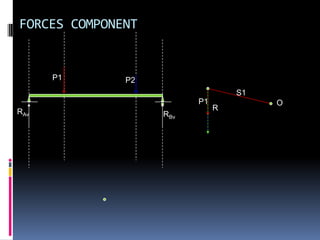
- 131. FORCES COMPONENT P1 P2 S1 P1 O RAv R RBv
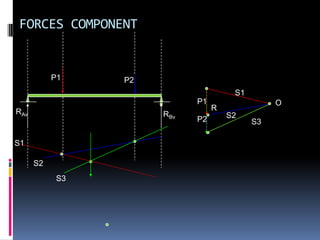
- 132. FORCES COMPONENT P1 P2 S1 P1 O RAv R RBv S2 P2 S3 S1 S2 S3
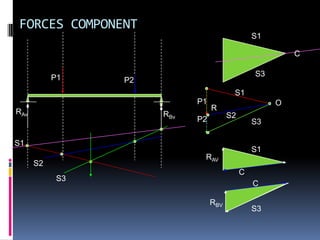
- 133. FORCES COMPONENT S1 C P1 S3 P2 S1 P1 O RAv R RBv S2 P2 S3 S1 C S1 RAV S2 C S3 C RBV S3
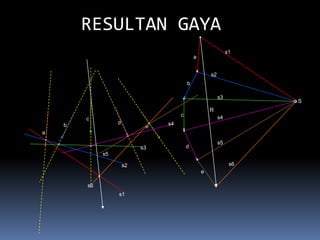
- 134. RESULTAN GAYA s1 a s2 b s3 S R c s4 c b d s4 e a s5 s3 d s5 s2 s6 e s6 s1
- 135. a b S R c c b d e a d e