Mi+ +bab+3+metode+transportasi
- 3. Model Transportasi ’ü¼ Dilihat dari namanya, metode transportasi digunakan untuk mengoptimalkan biaya pengangkutan (transportasi) komoditas tunggal dari berbagai daerah sumber menuju berbagai daerah tujuan. ’ü¼ Tiga hal penting harus diingat dari penjelasan di atas, yaitu komoditas tunggal, daerah sumber (asal) lebih dari satu dan daerah tujuan juga lebih dari satu. ’ü¼ Disamping kegunaannya untuk mengatur distribusi pengiriman barang, metode transportasi juga dapat digunakan untuk masalah-masalah lain misalnya, penjadwalan dalam proses produksi, penempatan persediaan atau pembelanjaan modal.
- 4. Data yang dibutuhkan dalam metode transportasi adalah: 1. Level suplai pada setiap daerah sumber dan level permintaan pada setiap daerah tujuan untuk kasus pendistribusian barang; jumlah produksi dan jumlah permintaan (kapasitas inventori) pada kasus perencanaan produksi. 2. Biaya transportasi per unit komoditas dari setiap daerah sumber menuju berbagai daerah tujuan pada kasus pendistribusian; biaya produksi dan inventori per unit pada kasus perencanaan produksi.
- 5. ’éĪ Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber, kecuali ada kendala lainnya. ’éĪ Kendala yang mungkin terjadi adalah tidak adanya jaringan transportasi dari suatu sumber menuju sutau tujuan; waktu pengangkutan yang lebih lama dibandingkan masa berlaku komoditas
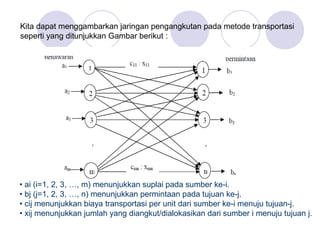
- 6. Kita dapat menggambarkan jaringan pengangkutan pada metode transportasi seperti yang ditunjukkan Gambar berikut : ŌĆó ai (i=1, 2, 3, ŌĆ”, m) menunjukkan suplai pada sumber ke-i. ŌĆó bj (j=1, 2, 3, ŌĆ”, n) menunjukkan permintaan pada tujuan ke-j. ŌĆó cij menunjukkan biaya transportasi per unit dari sumber ke-i menuju tujuan-j. ŌĆó xij menunjukkan jumlah yang diangkut/dialokasikan dari sumber i menuju tujuan j.
- 7. Dalam masalah transportasi, secara umum penyelesaian masalah dilakukan dengan dua tahap, yakni : ’éĪ Tahap 1, dengan penyelesaian awal, dimana metode yang dapat digunakan adalah : ┬Ę Metode NWC (North West Corner) ┬Ę Metode LC (Least Cost) ┬Ę Metode VAM (Vogel Aproximation Method) ┬Ę Metode RAM (Russel Aproximation Method) ’éĪ Tahap 2, Penyelesaian akhir, dengan metode : ┬Ę Stepping Stone ┬Ę MODI (Modified Distribution)
- 8. Contoh Soal : ’ü¼ Sebuah perusahaan Negara berkepentingan mengangkut pupuk dari tiga pabrik ke tiga pasar. Kapasitas penawaran ketiga pabrik, permintaan pada ketiga pasar dan biaya transport perunit adalah sebagai berikut:
- 9. ’éĪ Masalah diatas diilustrasikan sebagai suatu model jaringan pada gambar sebagai berikut:
- 10. Masalah diatas juga dapat dirumuskan sebagai suatu masalah LP sebagai berikut: ’éĪ Minimumkan: Z = 8X11 + 5X12 + 6X13 + 15X21 + 10X22 + 12X23 + 3X31 + 9X32 + 10X33 ’éĪ Batasan: X11 + X12 X21 + X22 X31 + X32 X11 + X21 X12 + X22 X13 + X23 + + + + + + X13 X23 X33 X31 X32 X33 = = = = = = 120 (penawaran pabrik 1) 80 (penawaran pabrik 2) 80 (penawaran pabrik 3) 150 (permintaan pabrik 1) 70 (permintaan pabrik 2) 60 (permintaan pabrik 3)
- 12. SOLUSI AWAL TRANSPORTASI 1. METODE NORTHŌĆōWEST CORNER Langkah-langkahnya adalah sebagai berikut: a. Mulai pada pojok kiri atas (barat laut table) dan alokasikan sebanyak mungkin tanpa menyimpang dari batasan penawaran dan permintaan. b. Hilangkan baris atau kolom yang tidak dapat dialokasikan lagi, kemudian alokasikan sebanyak mungkin ke kotak didekat baris atau kolom yang tidak dihilangkan, jika kolom atau baris sudah dihabiskan, pindahkan secara diagonal kekotak berikutnya. c. Lanjutkan dengan cara yang sama sampai semua penawaran telah dihabiskan dan keperluan permintaan telah dipenuhi. Solusi awal dengan menggunakan metode north ŌĆō west corner pada masalah diatas ditunjukkan oleh table 1.2.
- 13. Dari table 1.2 diatas dapat diketahui bahwa biaya transport total adalah sebagai berikut: Z = (8 x 120) + (15 x 30) + (10 x 50) + (9 x 20) + (10 x 60) = 2690 Ingat, ini hanya solusi awal, sehingga tidak perlu optimum.
- 14. 2. METODE LEAST-COST Langkah-langkahnya adalah sebagai berikut: a. Pilih variable Xij (kotak) dengan biaya transport (cij) terkecil dan alokasikan sebanyak mungkin. Ini akan menghabiskan baris i atau kolom j. b. Dari kotak-kotak sisanya yang layak (yaitu yang tidak terisi atau dihilangkan) pilih cij terkecil dan alokasikan sebanyak mungkin. c. Lanjutkan proses ini sampai semua penawaran dan permintaan terpenuhi. Solusi awal dengan menggunakan metode north ŌĆō west corner pada masalah diatas ditunjukkan oleh table 1.3.
- 15. Dari table 1.3 diatas dapat diketahui bahwa biaya transport total adalah sebagai berikut: Z = (3 x 80) + (5 x 70) + (6 x 50) + (12 x 10) + (15 x 70) = 2060
- 16. 3. METODE APROKSIMASI VOGEL (VAM) Proses VAM dapat diringkas sebagai berikut: a. Hitung opportunity cost untuk setiap baris dan kolom. Opportunity cost untuk setiap baris ke-i dihitung dengan mengurangkan nilai cij terkecil pada baris tersebut dengan nilai cij satu tingkat lebih besar pada baris yang sama. Opportunity cost kolom diperoleh dengan cara yang sama. Biaya-biaya ini adalah pinalti karena tidak memilih kotak dengan biaya minimum. b. Pilih baris atau kolom dengan opportunity cost terbesar (jika terdapat nilai kembar, pilih secara sembarang. Alokasikan sebanyak mungkin kekotak dengan nilai cij minimum pada baris atau kolom yang dipilih. c. Hilangkan semua baris dan kolom dimana penawaran dan permintaan telah dihabiskan. d. Jika semua penawaran dan permintaan belum dipenuhi, kembali kelangkah pertama dan hitung kembali opportunity cost yang baru. Solusi awal dengan menggunakan metode VAM pada masalah diatas ditunjukkan oleh table 1.4.
- 17. Biaya transport model VAM adalah sebagai berikut: Z = (3 x 80) + (8 x 70) + (6 x 50) + (10 x 70) + (12 x 10) = 1920 Biaya total untuk solusi awal dengan metode VAM merupakan biaya awal terkecil yang diperoleh dari ketiga metode solusi awal. Kenyataannya, solusi ini juga optimum, suatu keadaan yang akan ditunjukan pada pembahasan mencari solusi optimum.
- 18. MENENTUKAN SOLUSI OPTIMUM 1. METODE STEPPING STONE Beberapa hal penting yang perlu diperhatikan dalam penyusunan jalur stepping stone untuk mencari variable masuk. a. Arah yang diambil boleh searah atau berlawanan arah jarum jam. b. Hanya ada satu jalur tertutup untuk setiap kotak kosong. c. Jalur harus mengikuti kotak terisi, kecuali pada kotak kosong yang sedang dievaluasi. d. Baik kotak terisi maupun kotak kosong dapat dilewati dalam penyusunan jalur tertutup. e. Suatu jalur dapat melintasi dirinya. f. Sebuah penambahan dan pengurangan yang sama besar harus kelihatan pada setiap baris dan kolom pada jalur itu.
- 19. Proses jalur tertutup dalam prosedur stepping stone ditunjukan pada table berikut.
- 20. ŌĆó Penambahan atau pengurangan biaya dari jalur tertutup X12: C12 = 5 ŌĆō 10 + 15 ŌĆō 8 = +2 ŌĆó Penambahan atau pengurangan biaya dari jalur tertutup X13: C13 = 6 ŌĆō 10 + 9 ŌĆō 10 + 15 - 8 = +2 ŌĆó Penambahan atau pengurangan biaya dari jalur tertutup X23: C23 = 12 ŌĆō 10 + 9 ŌĆō 10 = +1 ŌĆó Penambahan atau pengurangan biaya dari jalur tertutup X31: C31 = 3 ŌĆō 15 + 10 ŌĆō 9 = -11 Analisis diatas menunjukan bahwa C31 memiliki perubahan biaya negative, sehingga X31 menjadi variable masuk. Jika terdapat dua atau lebih Xij dengan nilai Cij negative,maka pilih satu yang memiliki perubahan penurunan biaya terbesar (negative terbesar), dan jika terdapat nilai kembar, pilih sembarang.
- 23. Jumlah yang dialokasikan kedalam variable masuk dibatasi oleh permintaan dan penawaran, serta dibatasi pada jumlah minimum pada suatu kotak yang dikurangi pada jalur tertutup. Dari contoh diatas dapat diketahui bahwa variable X31 merupakan variable masuk, maka: X31 minimum = (X21, X32) = min (30, 20) = 20, sehingga table transportasi menjadi:
- 24. Solusi optimum dicapai disaat tidak ada calon variable masuk bernilai negative, dengan kata lain Cij bernilai positif. Solusi optimum dicapai melalui tiga iterasi:
- 26. Table 1.11 diatas memberikan nilai Cij positif untuk semua kotak kosong, sehingga tidak dapat diperbaiki lagi. Solusi optimum pada table 1.11 memberikan biaya transport terkecil, yaitu: Z = (8 x 70) + (6 x 50) + (10 x 70) + (12 x 10) + (3 x 80) = 1920
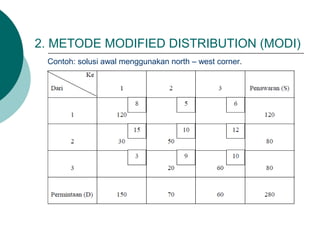
- 27. 2. METODE MODIFIED DISTRIBUTION (MODI) Contoh: solusi awal menggunakan north ŌĆō west corner.
- 28. Metode MODI memberikan Ui dan Vj yang dirancang untuk setiap baris dan kolom. Dari table diatas dapat diketahui bahwa: X11 : U1 + V1 = C11 = 8, misalkan U1 = 0, maka: 0 + V1 = 8, V1 = 8 X21 : U2 + V1 = C21 = 15 U2 + 8 = 15, U2 = 7 X22 : U2 + V2 = C22 = 10 7 + V2 = 10, V2 = 3 X32 : U3 + V2 = C32 = 9 U3 + 3 = 9, U3 = 6 X33 : U3 + V3 = C33 = 10 6 + V3 = 10, V3 = 4
- 29. ’éĪ Nilai perubahan untuk setiap variable non dasar Cij, ditentukan melalui: Cij = cij ŌĆō Ui ŌĆō Vj, sehingga: C12 = 5 ŌĆō 0 ŌĆō 3 = +2 C23 = 12 ŌĆō 7 ŌĆō 4 = 1 C13 = 6 ŌĆō 0 ŌĆō 4 = +2 C31 = 3 ŌĆō 6 ŌĆō 8 = -11 ’éĪ Nilai C31 negatif terbesar (-11) menunjukan bahwa solusi yang ada tidak optimal dan X31 sebagai variable masuk. Jumlah yang dialokasikan ke X31 ditentukan sesuai dengan prosedur stepping stone, selanjutnya Ui, Vj, dan Cij pada table baru dihitung kembali untuk uji optimalitas dan menentukan variable masuk.
- 30. REFERENSI 1. Sri Mulyono, Riset Operasi, Jakarta: Lembaga Penerbit Fakultas Ekonomi UI, 2002
- 31. Soal Tugas Dari tabel dibawah ini dapatkan hasil yang paling effisien dengan metode batu loncatan.
- 32. Soal 2 ’ü¼ Suatu Perusahaan memiliki 3 buah pabrik dan 3 buah gudang penjualan. Kebutuhan tiap gudan penjualan sebagai berikut : Jakarta 300 Ton Surabaya 400 Ton Bandung 500 Ton Kapasitas pabrik sebagai berikut : Semarang 200 Ton Magelang 650 Ton Solo 350 Ton Biaya dari pabrik ke gudang : ’ü¼ Dengan metode batu loncatan hitunglah Total biaya minimum.