MIRU2016 チュートリアル
?
30 likes?26,166 views
明日から使える凸最適化～近接分離最適化を中心に～＠MIRU2016 MATLAB code https://sites.google.com/site/thunsukeono/talks/MIRU2016_Ono.zip?attredirects=0&d=1
![画像と最適化（例：画像復元）
5
◆Tikhonov正則化による画像復元
隣接画素との差分のL2ノルム（＝滑らかさの評価）
観測との二乗誤差（Φ：ぼけ）
制約無し＋滑らかな凸関数 ? 微分＝０が最適解の特徴付け
この場合、↑の線型方程式系を解けば良い
観測 復元結果
イマイチ…
もっと柔軟に目的関数を設計したい
→ L2ノルムはエッジがなまる
制約条件も使いたい
→ 画素値は[0,255]の範囲とか
滑らかではない凸関数＋制約条件
を扱える最適化テクニックは？](https://image.slidesharecdn.com/miru2016tutorial-160801010500/85/MIRU2016-5-320.jpg)
![有用な距離射影の例
15
? BOX制約：
? L2ノルム球：
距離射影＝入力ベクトルの各要素を閉区間 [a, b] に押し込める
距離射影＝ベクトル v からみて入力ベクトル方向へ半径 ε だけ動く](https://image.slidesharecdn.com/miru2016tutorial-160801010500/85/MIRU2016-15-320.jpg)
![式変形2/3
25
? 目的関数の変数をproxが計算できる関数ごと
に分離 z = [z1
T z2
T z3
T]T
? 元の関係性を満たすよう を定義](https://image.slidesharecdn.com/miru2016tutorial-160801010500/85/MIRU2016-25-320.jpg)
![宣伝：ブロック核型ノルム（ADMM）
38
応用：画像の構造ーテクスチャ分離
POINT：テクスチャのパターンを局所的な低ランク性でモデル化
image
cartoon
texture
cartoon
texture
[Schaeffer-Osher 2013] 提案
S. Ono et al., “Cartoon-texture image decomposition using blockwise low-rank texture characterization,” IEEE Trans. Image Process., 2014.](https://image.slidesharecdn.com/miru2016tutorial-160801010500/85/MIRU2016-38-320.jpg)
MIRU2016 チュートリアル
- 3. 凸最適化問題とは 3 凸関数：目的関数 凸集合：制約条件 凸 非凸 関数 集合 QESTION: なぜ凸最適化? ANSWER: 局所最適解＝大域的最適解 ? 最適解を効率的に計算可能 ? 初期値に非依存 ? 問題設計の良し悪しの判断が比較的容易
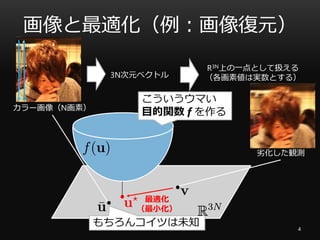
- 5. 画像と最適化（例：画像復元） 5 ◆Tikhonov正則化による画像復元 隣接画素との差分のL2ノルム（＝滑らかさの評価） 観測との二乗誤差（Φ：ぼけ） 制約無し＋滑らかな凸関数 ? 微分＝０が最適解の特徴付け この場合、↑の線型方程式系を解けば良い 観測 復元結果 イマイチ… もっと柔軟に目的関数を設計したい → L2ノルムはエッジがなまる 制約条件も使いたい → 画素値は[0,255]の範囲とか 滑らかではない凸関数＋制約条件 を扱える最適化テクニックは？
- 6. 今日のお話 6 連続最適化 単調写像理論 （非拡大写像、不動点） 凸最適化 近接分離 （proximal splitting） に基づく凸最適化 ADMM近接勾配法 主-双対近接分離法 深層学習にも応用 G. Taylor et al. “Training Neural Networks Without Gradients: A Scalable ADMM Approach,” ICML 2016.
- 7. WHY 近接分離最適化？ 7 ? 所望の信号に対する先験的性質の活用 ? スパース、低ランク、平滑性、etc… を微分 できない凸関数で良好に評価可能 ? 制約条件の取り扱いが比較的容易 ? 範囲制約、部分空間所属、ノルム制約、etc… を柔軟に課すことが可能 ? 大規模な問題(N > 10^4)に対応可能 ? 勾配降下 and/or 近接写像が基本骨子 ? L1ノルム等の応用上有用な凸関数の近接写像 が非常に効率的に計算可能
- 8. 特定のアルゴリズムを応用事例とともに解説し 明日からでも使えるようになることを目指します 注意点 ? 参考文献は最後にまとめて紹介します ? 使い方にフォーカスする＆記述を簡潔にするため、厳密性を犠牲にしてい る部分があります ? 理論的な収束条件等に興味がある方は、途中でご質問いただくか、末尾の 参考文献をご参照ください
- 10. 勾配降下 (gradient descent) 10 支持超平面 (supporting hyperplane) 滑らか（微分可能）な凸関数 f (smooth convex function) ? 現在の推定値 x(n) から関数 f の勾配?f の逆方向へ更新 ? これの反復→いわゆる最急降下法 (steepest descent method) ? f が滑らかな凸関数であれば最適解へ収束（with 適切な γ ） 支持超平面を 急降下する方向
- 11. 近接写像 (proximity operator) 11 ? 凸関数 f + 現在の推定値 x(n) との二乗誤差の最小化＝prox ? つまり、近接写像の計算自体が一種の最適化→本末転倒では？ ? 幸運な事に、いくつかの凸関数 f の prox が効率的に計算可能 ※ 以降、このような関数を prox可能 とよぶ 滑らかでない凸関数 f (nonsmooth convex function) 近接写像を定義 →一意に定まる！ 支持超平面が一意に定まらない ＝微分できない
- 12. 有用な近接写像 (prox) の例 ? L1ノルム # L0擬ノルムの最良凸緩和→スパース性の評価 # 統計的には事前分布＝ラプラス分布 ? 混合L1,2ノルム 近接写像＝ソフト閾値処理＝各要素の絶対値を削る 符号関数 要素ごとの積 各要素の絶対値 近接写像＝サブベクトルごとに異なるスケールでソフト閾値処理 k 番目のサブベクトル x を K個のサブベクトルへ分割 (K=NのときL1ノルムに一致) 12 L0 L1
- 13. 有用な近接写像（prox）の例 13 ? 核型ノルム (nuclear norm) 特異値（singular value) 非ゼロの特異値の数（非凸） rank(M)の最良凸緩和 近接写像＝特異値にソフト閾値処理 特異値分解：
- 14. 距離射影 (metric projection) 14 閉凸集合 C の指示関数 (indicator function)： を用いると距離射影は近接写像の一例とみなせる 現在の推定値からC内の 最も近い点へ移動 閉凸集合 C (closed convex set)
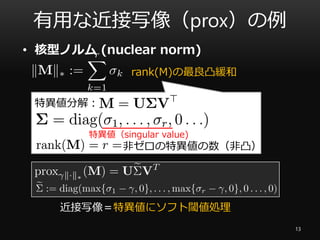
- 15. 有用な距離射影の例 15 ? BOX制約： ? L2ノルム球： 距離射影＝入力ベクトルの各要素を閉区間 [a, b] に押し込める 距離射影＝ベクトル v からみて入力ベクトル方向へ半径 ε だけ動く
- 16. 近接勾配法によるスパース信号復元
- 17. 近接勾配法とは 17 ◆対象とする凸最適化問題 微分可能 (勾配はβ-リプシッツ連続) 近接写像が効率的に計算可能 ◆近接勾配法 (proximal gradient, forward-backward splitting,…) ? f の勾配降下→ g の近接写像の繰り返し ? g := 指示関数 とすれば射影勾配法と一致 ? 勾配法に対する加速テクニックを適用可能 →FISTA (詳しくは末尾の文献を参照)
- 18. スパース信号復元問題 18 ◆観測モデル ◆最適化問題：L1ノルム最小化に基づくスパース信号復元 観測ベクトル 観測過程を 記述する行列 加法性雑音 推定したい信号 仮定：スパース (ほとんどの要素が0/ほぼ0) データ項 スパース項（L1ノルム） ? いわゆる圧縮センシングやLASSOもこの定式化 ? 目的関数が微分不可能（通常の勾配法では無理） ? POINT: L1ノルムの近接写像は簡単に計算可能
- 19. 近接勾配法によるスパース信号復元 19 ◆近接勾配法に基づくアルゴリズム (通称 ISTA) L1ノルムの近接写像 prox＝ソフト閾値処理 要素ごとに絶対値を削る処理＝O(N) で計算可能 ※近接勾配法の一般形式
- 20. ADMMによるロバスト主成分分析 (robust principal component analysis)
- 21. ◆対象とする凸最適化問題 ADMMとは L2の二乗 近接写像 ※ d は双対変数に相当 ◆ADMM (Alternating Direction Method of Multipliers) 近接写像が効率的に計算可能二次関数 フル列ランク行列 21 POINT：線型制約 z = Gu をうまく利用することで近接勾配法 では無理だった微分できない凸関数の和の最小化を扱える
- 24. 式変形1/3 24 指示関数 (indicator function) を導入 → 制約条件を目的関数表現
- 25. 式変形2/3 25 ? 目的関数の変数をproxが計算できる関数ごと に分離 z = [z1 T z2 T z3 T]T ? 元の関係性を満たすよう を定義
- 26. 式変形3/3 26 ? L2の二乗がある場合は へ（今回は無し） ? 残りは全て にまかせる めでたくADMMが適用できる形に帰着
- 27. 各ステップの計算 (1/2) 27 L2最小化＆Gがフル列ランク =>微分＝0 として解析的に解ける ? 今回は G が単純な構造なので逆行列計算も無し ? GTGがBCCB構造→FFTによる高速計算 O(NlogN) ? GTGがスパース→共役勾配法等を利用 に注意すると
- 28. 各ステップの計算 (2/2) 28 prox の計算を zi ごとに分離できる ? 各々のproxを個別に 計算すれば良い に注意すると
- 29. 実際のアルゴリズムをまとめると 29 ADMMの 一般形 Robust PCA 用のADMM SVDして特異値にソフト閾値処理 普通のソフト閾値処理 D = {M} なので常にM 微分＝０を解析的に解いた結果
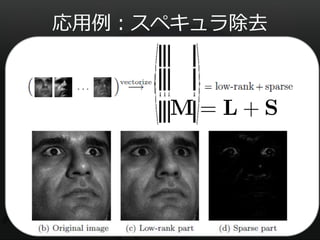
- 30. 応用例：スペキュラ除去 30
- 31. 主-双対近接分离法による画像復元
- 32. ◆対象とする最適化問題 主-双対近接分離法とは ※ y は双対変数 ◆主-双対近接分離法 (primal-dual splitting) 微分可能 (勾配はβ-リプシッツ連続) 近接写像が効率的に計算可能近接写像が効率的に計算可能 h の凸共役の近接写像→ h の近接写像を用いて表現可能 Moreau’s Identity POINT：f の勾配、g, h の近接写像、 の計算のみ → 逆行列計算を回避可能（でもADMMより収束は遅め） 32
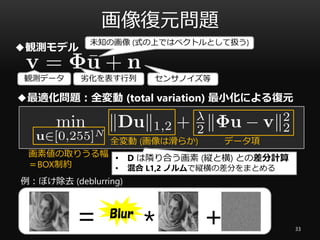
- 33. 画像復元問題 33 例：ぼけ除去 (deblurring) +*Blur = 観測データ ◆観測モデル 劣化を表す行列 未知の画像 (式の上ではベクトルとして扱う) センサノイズ等 全変動 (画像は滑らか) データ項 ◆最適化問題：全変動 (total variation) 最小化による復元 画素値の取りうる幅 ＝BOX制約 ? D は隣り合う画素 (縦と横) との差分計算 ? 混合 L1,2 ノルムで縦横の差分をまとめる
- 35. 実際のアルゴリズム ◆主-双対近接分離法の一般形 ◆画像復元用の主-双対近接分離法 BOX制約への距離射影 共役関数の prox 計算のため仲介変数を導入 元の関数の prox (グループソフト閾値処理) 34
- 37. 結局どのアルゴリズムがいいの？ 37 解きたい問題が f(x) + g(x) と表わせ、fが微分可能、gがprox可能 YES 近接勾配法 (with 加速) NO 解きたい問題が f(x) + g(Lx) (または f(x) + g(y) s.t. Lx=y) と表わせ、 fがL2の二乗、gがprox可能、LTLの逆行列が効率的に計算可能 YES ADMM NO 主-双対近接分離法 NOTE: と表現できる つまり、任意個のprox可能な凸関数の和は g と L にまとめられる ここで、各 gi は prox可能、
- 38. 宣伝：ブロック核型ノルム（ADMM） 38 応用：画像の構造ーテクスチャ分離 POINT：テクスチャのパターンを局所的な低ランク性でモデル化 image cartoon texture cartoon texture [Schaeffer-Osher 2013] 提案 S. Ono et al., “Cartoon-texture image decomposition using blockwise low-rank texture characterization,” IEEE Trans. Image Process., 2014.
- 39. 宣伝：色線形性に基づく正則化（ADMM） 39 全変動のみ原画像 PSNR: 22.17 PSNR: 26.14 応用：圧縮センシング再構成（２割の情報から復元） POINS：カラー画像の局所的な色線形性を重み付き核型ノルムでモデル化（非凸） 全変動＋提案 S. Ono & I. Yamada “Color-line regularization for color artifact removal,’’ IEEE Trans. Comput. Imag., 2016.
- 40. 宣伝：グラフ信号用の一般化全変動（PDS） 40 Original Noisy (sigma = 0.05) Noisy (sigma = 0.1) GTV (RMSE = 1.80e-3) GTV (RMSE = 2.95e-3) GTGV (RMSE = 1.40e-3) GTGV (RMSE = 2.20e-3) 応用：歪んだメッシュを平滑化 ? グラフ構造は三角メッシュ ? 信号 = xyz座標 (これが歪んでいる) ? グラフ信号用全変動と比較 S. Ono et al., “Total generalized variation for graph signals,” ICASSP 2015.
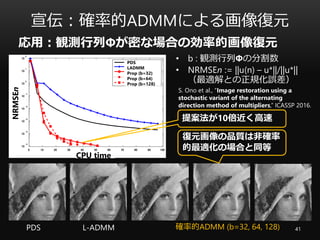
- 41. 宣伝：確率的ADMMによる画像復元 41L-ADMMPDS 確率的ADMM (b=32, 64, 128) ? b : 観測行列Φの分割数 ? NRMSEn := ||u(n) – u*||/||u*|| （最適解との正規化誤差） 提案法が10倍近く高速 CPU time NRMSEn PDS LADMM Prop (b=32) Prop (b=64) Prop (b=128) S. Ono et al., “Image restoration using a stochastic variant of the alternating direction method of multipliers,” ICASSP 2016. 復元画像の品質は非確率 的最適化の場合と同等 応用：観測行列Φが密な場合の効率的画像復元
- 42. まとめ 42 ◆今回紹介した近接分離系の凸最適化アルゴリズム ? 近接勾配法 (proximal gradient, forward-backward splitting) 特徴：適用範囲は狭めだが大幅な加速が可能 ? ADMM (Alternating Direction Method of Multipliers) 特徴：適用範囲が広く収束もそれなりに速い ? 主-双対近接分離法 (primal-dual splitting) 特徴：適用範囲が広く逆行列計算を回避できるが収束は遅め (計量のせい) ? 近接写像と勾配降下を基本骨子とするアルゴリズム → L1ノルムなどの応用上有用な非可微分凸関数を扱える → 画像などの高次元変数でも現実的な計算量を担保 → 制約条件の扱いも比較的自由 ? フレキシブルに目的関数?制約を設計できるため、工夫 次第で様々な応用が可能 POINT
- 43. 参考文献 (1/4) 43 ◆近接勾配法 (proximal gradient, forward-backward splitting) 1. G. B. Passty, “Ergodic convergence to a zero of the sum of monotone operators in Hilbert space,” J. Math. Anal. Appl., 1979. (原著) 2. G. Chen & R. T. Rockafellar, “Convergence rates in forward–backward splitting,” SIAM J. Optim., 1997. (収束レート解析) 3. P. L. Combettes & V. R. Wajs, ”Signal recovery by proximal forward–backward splitting,” SIAM Multiscale Model. Simul., 2005. (更なる理論的整備) 4. A. Beck & M. Teboulle, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imag. Sci., 2009. (通称 FISTA, Nesterov の optimal gradient を融合) 5. M. Yamagishi & I. Yamada, “Over-relaxation of the fast iterative shrinkage- thresholding algorithm with variable stepsize,” Inverse Probl., 2011. (FISTA のス テップサイズ拡張) 6. I. Daubechies et al., “An iterative thresholding algorithm for linear inverse problems with a sparsity constraint,” Comm. Pure Appl. Math., 2004. (スパース復 元応用) 7. J. Duchi & Y. Singer, “Efficient online and batch learning using forward- backward splitting,” J Mach. Learn. Res., 2009. (機械学習応用)
- 44. 参考文献 (2/4) 44 ◆ADMM (Alternating Direction Method of Multipliers) 1. D. Gabay & B. Mercier, “A dual algorithm for the solution of nonlinear variational problems via finite elements approximations,” Comput. Math. Appl., 1976. (原著) 2. J. Eckstein & D. P. Bertsekas, “On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators,” Math. Program., 1992. (Dougal-Rachford splittingに基づく導出と理論的整備) 3. B. He & X. Yuan “On the O(1/n) Convergence Rate of the Douglas–Rachford Alternating Direction Method,” SIAM J. Numer. Anal., 2012. (収束レート) 4. S. Boyd et al., “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. Trends Mach. Learn., 2011. (分散最適化?機械学習適用とレビュー) 5. M. Afonso et al. “An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems,” IEEE Trans. Image Process., 2011. (画像復元応用) 6. S. Ono et al., “Cartoon-texture image decomposition using blockwise low-rank texture characterization,” IEEE Trans. Image Process., 2014. (画像分離応用) 7. S. Ono et al., “Image restoration using a stochastic variant of the alternating direction method of multipliers,” ICASSP 2016. (確率的ADMMの画像復元応用） 8. S. Ono & I. Yamada “Color-line regularization for color artifact removal,’’ IEEE Trans. Comput. Imag., 2016. (色線形性正則化，非凸応用）
- 45. 参考文献 (3/4) 45 ◆主-双対近接分離法 (primal-dual splitting, PDS) 1. A. Chambolle & T. Pock, “A first-order primal-dual algorithm for convex problems with applications to imaging,” J. Math. Imag. Vis., 2011. (原著、少し限 定的な形) 2. L. Condat, “A primal-dual splitting method for convex optimization involving Lipschitzian, proximable and linear composite terms,” J. Optim. Theory Appl., 2013. (原著、今回紹介した形) 3. R. Bo? & E. Csetnek, “On the convergence rate of a forward-backward type primal-dual splitting algorithm for convex optimization problems,” Optimization, 2015. (収束レート) 4. S. Ono and I. Yamada, “A convex regularizer for reducing color artifact in color image recovery,” CVPR 2013. (色ムラ?偽色除去) 5. S. Ono and I. Yamada, “Decorrelated vectorial total variation,” CVPR, 2014. (カ ラー画像処理応用) 6. S. Ono, M. Yamagishi, and I. Yamada, “A sparse system identification by using adaptively-weighted total variation via a primal-dual splitting approach,” ICASSP 2013. (adaptive版) 7. S. Ono, I. Yamada, and I. Kumazawa, “Total generalized variation for graph signals,” ICASSP 2015. (グラフ信号処理応用) 8. S. Ono and I. Yamada, “Hierarchical convex optimization with primal-dual splitting,” IEEE Trans. Signal Process., 2015. (PDSを利用した階層型最適化)
- 46. 参考文献 (4/4) 46 ◆その他、関係する and/or 役立つと思われる文献?書籍 1. J. J. Moreau, “Fonctions convexes duales et points proximaux dans un espace Hilbertien,” (in French) C. R. Acad. Sci. Paris Ser. AMath., 1962. (近接写像初出) 2. H. H. Bauschke & P. L. Combettes, Convex analysis and monotone operator theory in Hilbert spaces. Springer, 2011. (凸解析と単調写像理論の関係について 体系的にまとめた良書、議論は基本的に無限次元ヒルベルト空間で展開) 3. P. L. Combettes & J.-C. Pesquet, “Proximal splitting methods in signal processing,” in Fixed-Point Algorithm for Inverse Problems in Science and Engineering, Springer-Verlag, 2011. (近接分離最適化のレビュー、近接写像が効率 的に計算可能な凸関数のリスト) 4. I. Yamada et al., “Minimizing the Moreau envelope of nonsmooth convex functions over the fixed point set of certain quasi-nonexpansive mappings,” in Fixed-Point Algorithm for Inverse Problems in Science and Engineering, Springer- Verlag, 2011. (いくつかの近接分離系の手法を非拡大写像の不動点的視点から解説) 5. N. Parikh & S. Boyd, “Proximal algorithms,“ Foundations and Trends in Optimization, 2014. (近接分離最適化のレビュー） 6. S. Ono & I. Yamada, “Signal recovery with certain involved convex data-fidelity constraints,” IEEE Trans. Signal Process., 2015. (近接分離系の手法では扱えないデー タ忠実性制約が課された信号復元問題を解く最適化アルゴリズムの提案)