![Return indeks pasar (RM) dan kesalahan residu
untuk setiap sekuritas (ei) merupakan variabelvariabel acak. Oleh karena itu, ei tidak berkovari
dengan return indeks pasar, RM. Asumsi ini
dapat dinyatakan secara matematis sebagai:
Cov (ei,RM) = 0
E (ei.[RM-E(RM)]) = 0](https://image.slidesharecdn.com/modelindekstunggalppt-140106170553-phpapp01/85/Model-indeks-tunggal-ppt-9-320.jpg)
![Period
e ke-t
1
2
3
4
5
6
7
eA,t = RA,t - 留A (A . RM,t)
eA,1=0,060-0,0216-(1,7.0,040)=-0,0296
2.
eA,2=0,077-0,0216-(1,7.0,041)=-0,0143
E(eA) = (-0,0296-0,0143-0,0116+0,0779
eA,3=0,095-0,0216-(1,7-0,050)=-0,0116
+0,0001-0,0191-0,0031) / (7-1)
eA,4=0,193-0,0216-(1,7-0,055)=0,0779
=0
eA,5=0,047-0,0216-(1,7-0,015)=0,0001
eA,6=0,113-0,0216-(1,7-0,065)=0,0191
eA,7=0,112-0,0216-(1,7-0,055)=0,0031
3. 2 = [(0,0296 0)2 + (0,0143 0)
+(-0,0116-0)2 + (0,0779 0)2
+(0,0001-0)2 + (0,0191 0)2
+(-0,0031-0)2 ]/(7 1)
= 0,0068/6
. =
= 0,00128
, , + , ,
+ (, , ) + , ,
+ , , + , ,
+ , , /( )
= , / = ,](https://image.slidesharecdn.com/modelindekstunggalppt-140106170553-phpapp01/85/Model-indeks-tunggal-ppt-14-320.jpg)
![5a.total resiko berdasarkan model indeks tunggal
2 = 2 . 2 + 2
= 1,7 2 . 0,00026 + 0,00128
= 0,002
b. Total resiko berdasarkan varian retrun sekuritas
2 = [(0,060 0,09957)2 + 0,077 0,09957 2
+ 0,095 0,09957 2 + 0,193 0,09957 2
+ 0,047 0,09957 2 + 0,113 0,09957 2
+ 0,112 0,09957 2 ]/(7 1)
= 0,002](https://image.slidesharecdn.com/modelindekstunggalppt-140106170553-phpapp01/85/Model-indeks-tunggal-ppt-15-320.jpg)
Model indeks tunggal ppt
- 1. MODEL INDEKS TUNGGAL KELOMPOK 7 NAMA ANGGOTA : 1. 2. 3. 4. 5. 6. 7. 8. OCTAVIA ENDANG PUNGKY RETNO.P. ANISA NUR HAYATI YULIANA KRISTANTI.H. YOGI YUDHA P. DEVY FITRIAWAN RAMA SAN CAHYA JAN QOMATULLAH
- 2. William Sharpe mengembangkan model yang disebut dengan model indeks tunggal. Dimana model ini digunakan untuk menyederhanakan perhitungan di model Markowitz dan juga digunakan untuk menghitung return ekspektasian dan risiko portofolio.
- 3. MODEL INDEKS TUNGGAL Model indeks tunggal didasarkan pada pengamatan bahwa harga dari suatu sekuritas berfluktuasi searah dengan indeks pasar. Hal ini menyarankan bahwa return-return dari sekuritas mungkin berkorelasi karena adanya reaksi umum (common response) terhadap perubahan-perubahan nilai pasar.
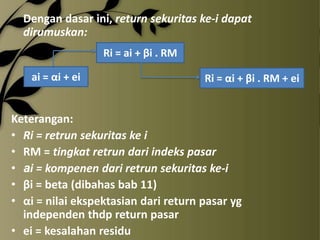
- 4. Dengan dasar ini, return sekuritas ke-i dapat dirumuskan: Ri = ai + 硫i . RM ai = 留i + ei Ri = 留i + 硫i . RM + ei Keterangan: Ri = retrun sekuritas ke i RM = tingkat retrun dari indeks pasar ai = kompenen dari retrun sekuritas ke-i 硫i = beta (dibahas bab 11) 留i = nilai ekspektasian dari return pasar yg independen thdp return pasar ei = kesalahan residu
- 5. Komponen Model Indeks Tunggal Model indeks tunggal membagi return sekuritas ke dalam dua komponen utama, yaitu: 1.Komponen return yang unik dan independen terhadap return pasar (留i). 2.Komponen return yang berhubungan dengan return pasar (硫i).
- 6. Model indeks tunggal juga dinyataka dalam retrun ekspektasian, dirumuskan: E(Ri) = E(留i) + E(硫i . RM) + E(ei) E(Ri) = 留i + 硫i . E(RM) Contoh: Diketahui return ekspektasian dari indeks pasar adalah 25%. Bagian dari retrun ekspaktasian suatu sekuritas yg independen thdp pasar (留i) adalah 4% dan 硫i sebesar 0,75. Ternyata return realisasi sebesar 26%.
- 7. Jawaban: E(Ri) = 留i + 硫i . E(RM) E(Ri) = 4% + 0,75 . 25% E(Ri) = 22,75% Jadi nilai retrun realisasi berdasarkan model indeks tunggal adalah Ri = 22,75% + ei. Dan kesalahan estimasi (ei) adalah sebesar 26% - 22,75% = 3,25% Jika nilai retrun realisasinya sama dengan nilai retrun yang diharapkan, maka investor mengestimasi retrun ekspektasian tanpa kesalahan.
- 8. Asumsi Model Indeks Tunggal Kesalahan residu dari sekuritas ke-i tidak berkovari dengan kesalahan residu sekuritas ke-j atau ei tidak berkovari (berkorelasi) dengan ej untuk semua nilai dari i dan j. Asumsi ini secara matematis dapat dituliskan sebagai: Cov (ei,ej) = 0 E (ei.ej) = 0
- 9. Return indeks pasar (RM) dan kesalahan residu untuk setiap sekuritas (ei) merupakan variabelvariabel acak. Oleh karena itu, ei tidak berkovari dengan return indeks pasar, RM. Asumsi ini dapat dinyatakan secara matematis sebagai: Cov (ei,RM) = 0 E (ei.[RM-E(RM)]) = 0
- 10. VARIAN RETURN SEKURITAS MODEL INDEKS TUNGGAL Secara umum varians return dari suatu sekuritas sebagai berikut: Ri = 留i + 硫i . RM + ei disubtitusikan E(Ri) = 留i + 硫i . E(RM) Maka rumus varian return sekuritas berdasarkan model indekstunggal sebagai berikut:
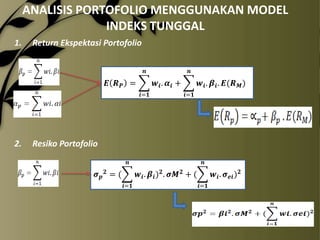
- 11. Resiko (varian retrun) sekuritas yang dihitung berdasarkan model ini terdiri dari dua bagian: 1. Resiko yang berhubungan dengan pasar (market related risk), yaitu: 2. Resiko untuk masing masing perusahaan (unique rsik), yaitu:
- 12. Contoh A: Retrun saham PT.A dan return indeks pasar selama 7 periode dan rata-rata aritmatikanya adalah sebagai berikut: Periode Retrun saham Retrun Indeks ke-t PT.A (RA) Pasar (RM) 1 2 3 4 5 6 7 0,060 0,077 0,095 0,193 0,047 0,113 0,112 0,040 0,041 0,050 0,055 0,015 0,065 0,055 Rata-rata aritmatika 0,09957 0,04586 Diketahui 留i dan 硫i adalah konstan dari waktu ke waktu. Dan 硫A untuk sekuritas PT.A adalah 1,7.
- 13. Hitunglah : 1. 2. 3. 4. 5. 1. Nilai ekspektasian PT.A (留A) Nilai ekspektasian dari kesalahan residu E(eA) Varian dari kesalahan residu Varian dari retrun pasar Total resiko berdasarkan model indeks tunggal dan varian retrun sekuritas.
- 14. Period e ke-t 1 2 3 4 5 6 7 eA,t = RA,t - 留A (A . RM,t) eA,1=0,060-0,0216-(1,7.0,040)=-0,0296 2. eA,2=0,077-0,0216-(1,7.0,041)=-0,0143 E(eA) = (-0,0296-0,0143-0,0116+0,0779 eA,3=0,095-0,0216-(1,7-0,050)=-0,0116 +0,0001-0,0191-0,0031) / (7-1) eA,4=0,193-0,0216-(1,7-0,055)=0,0779 =0 eA,5=0,047-0,0216-(1,7-0,015)=0,0001 eA,6=0,113-0,0216-(1,7-0,065)=0,0191 eA,7=0,112-0,0216-(1,7-0,055)=0,0031 3. 2 = [(0,0296 0)2 + (0,0143 0) +(-0,0116-0)2 + (0,0779 0)2 +(0,0001-0)2 + (0,0191 0)2 +(-0,0031-0)2 ]/(7 1) = 0,0068/6 . = = 0,00128 , , + , , + (, , ) + , , + , , + , , + , , /( ) = , / = ,
- 15. 5a.total resiko berdasarkan model indeks tunggal 2 = 2 . 2 + 2 = 1,7 2 . 0,00026 + 0,00128 = 0,002 b. Total resiko berdasarkan varian retrun sekuritas 2 = [(0,060 0,09957)2 + 0,077 0,09957 2 + 0,095 0,09957 2 + 0,193 0,09957 2 + 0,047 0,09957 2 + 0,113 0,09957 2 + 0,112 0,09957 2 ]/(7 1) = 0,002
- 16. KOVARIAN RETURN ANTARA SEKURITAS MODEL INDEKS TUNGGAL Rumus kovarian retrun antar dua sekuritas: = Ri,j = 留i + 硫i . RM + ei E(Ri,j) = 留i + 硫i . E(RM) 告 告 . 告 告 disubtitusikan = . . Contoh : Dua buah sekuritas A dan B masing-masing mempunyai Beta yaitu 硫A=1,7 dan 硫B=1,3. Varian return dari indeks pasar diketahui sebesar 0,00026. Kovarian antara sekuritas A dan B adalah : Jawab : ij= 硫A . 硫B . M族 = 1,7 . 1,3 . 0,00026 = 0,00057
- 17. PARAMETER PARAMETER INPUT UNTUK MODEL MARKOWITZ Model indeks tunggal dapat digunakan untuk menghitung return ekspektasi (E(Ri)), varians dari sekuritas (i2), dan kovarians antar sekuritas (ij) yang merupakan parameter-parameter input untuk analisis portofolio menggunakan model Markowitz.
- 18. Contoh B: Periode Ke-t Return saham PT A (RA) Return saham PT B (RB) Return index Pasar (RM) 1 2 3 4 5 6 7 0,060 0,077 0,095 0,193 0,047 0,113 0,112 0,15 0,25 0,30 0,40 0,27 0,15 0,55 0,040 0,041 0,050 0,055 0,015 0,065 0,055 Rata-rata 0,09957 0,2957 0,04586 Setelah perhitungan seperti contoh A : Diketahui : 署 = 1,7, 2 = 0,02, 2 = 0,00026, 署 = 1,3, 2 = 0,01998, . = 0,5
- 19. Hitunglah 1) Kovarian antara return PT.A dan PT.B 2) Resiko portofolio berdasarkan model indeks tunggal Jawab : 1.. = 倹. 倹. = 1.7.1,3.0,00026 = 0,00057 2. = 情 . + 情 . + . . . = (, ) . , + (, ) . , + . , . , . , = 0,0035
- 20. ANALISIS PORTOFOLIO MENGGUNAKAN MODEL INDEKS TUNGGAL 1. Return Ekspektasi Portofolio 告 = . + = 2. . . ( ) = Resiko Portofolio =( . ) . + ( = . ) =
- 21. Contoh C: Jumlah sekuritas (n) 1 2 3 4 5 6 7 8 9 10 20 50 100 200 500 1,000 5,000 10,000 jumlah parameter yang harus dihitung model Makrowitz model indeks tunggal n + (n.(n-1)/2 (2.n+1) 1 3 6 10 15 21 28 36 45 55 210 1,275 5,050 20,100 125,250 500,500 12,502,500 50,005,000 3 5 7 9 11 13 15 17 19 21 41 101 201 401 1,001 2,001 10,001 20,001
- 22. Dari contoh A dan B, telah dihitung besarnya = , , = , dan = , . diketahui = , , = , , wA = 0,5 dan wB = 0,5. Maka risiko portofolio yg dihitung berdasarkan model indeks tunggal: =( . ) . + ( = . ) = = (, . , + , . , ) . , + (, . , + , . , ) = 0,000585 + 0,0001084 = 0,0006934 Semakin banyak sekuritas dalam portofolio maka nilai resiko yang tidak sistematik akan semakin kecil nilainya dan akan bernilai nol jika jumlah sekuritas semakin besar. Resiko portofolio yang terdiversifikasi dengan baik hanya terdiri dari unsur sistematik saja. = .
- 23. MODEL PASAR Merupakan bentuk dari model indeks tunggal dengan batasan yang lebih sedikit. Bentuk model pasar yang sama dengan bentuk model indeks tunggal mempunyai return dan return ekspektasian sebagai berikut : Ri = 留i + 硫i . RM + ei dan E(Ri) = 留i + 硫i . E(RM)
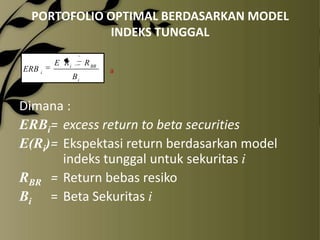
- 24. PORTOFOLIO OPTIMAL BERDASARKAN MODEL INDEKS TUNGGAL ERB i E Ri R BR Bi a Dimana : ERBi= excess return to beta securities E(Ri)= Ekspektasi return berdasarkan model indeks tunggal untuk sekuritas i RBR = Return bebas resiko Bi = Beta Sekuritas i
- 25. Langkah-langkah untuk menentukan besarnya titik pembatas adalah sebagai berikut : 1. Urutkan sekuritas berdasarkan nilai ERB terbesar ke kecil, yang terbesar merupa-kan kandidat untuk dimasukkan ke dalam Portofolio Optimal 2. Hitung nilai Ai dan Bi untuk masing-masing sekuritas ke i, sebagai berikut Ai E Ri R BR . B i 2 ei 2.a Bi Bi 2 ei 2.b
- 26. 3. Menghitung nilai Ci 2 Ci m 1 Ai 2 m Bi 3.a m2 = varian dari return Indeks Pasar. Dengan mensubstitusikan nilai Ai dan Bi maka rumus Ci menjadi C* 4. Besarnya cut off point (C*) adalah nilai Ci yang terbesar Sekuritas yang membentuk Portofolio Optimal adalah sekuritas yang mem-punyai nilai ERB lebih besar atau sama nilainya. ERB di titik C* adalah nilai ERB yang kecil, tidak disertakan dalam pem-bentukan Portofolio Optimal.
- 27. 5. Menentukan besarnya proporsi sekuritas xi wi zi 5.a xi i 2 ei ERB i C* 5.b wi = Proporsi Sekuritas k = jumlah sekuritas di portofolio = beta sekuritas ke-i i 2 = varian dari kesalahan residu sekuritas ke-i ei ERBi=excess retrun to Beta sekuritas ke-i C* =nilai Ci terbesar
- 28. Contoh D: Nilai Saham E(Ri) Bi ei^2 ERBi A B C D E 20 19 27 23 25 2,00 1,50 2,00 1,50 1,80 5,0 4,0 7,5 5,0 2,0 5 6 8,5 8,677 8,333 Diketahui: 1. Retrun aktiva bebas resiko (RBR)=10% 2. Varian indeks pasar = 10% Untuk masing masing sekuritas dapat dihitung yg hasilnya disajikan ditabel berikut: Nama E(Ri) Bi Saham ERBi Ai Bi = D C E B A 23 27 25 19 20 1,50 2,00 1,80 1,50 2,00 5,0 7,5 2,0 4,0 5,0 8,677 8,5 8,33 6 5 3,9 4,533 13,5 3,375 4 0,45 0,533 1,62 0,563 0,8 3,9 8,433 21,933 25,308 29,308 Ci = 0,45 0,983 2,603 3,166 3,966 7,091 7,787 8,114 7,749 7,208
- 29. Perhitungan: E Ri Ai R BR . B i 2 ei 23 Ai 10 . 1, 50 Bi 3 ,9 Bi 2 2 ei 1, 50 2 0 , 45 5,0 5,0 i Aj Ai Ai sebelumnya 2 m j 1 Ci i Bj Bi 1 Ai 2 m Bi Bi sebelumnya j 1 Sekuritas yang membentuk portofolio optimal adalah sekuritas yang mempunyai Erb lebih besar dari Ci, yaitu sekuritas D, C, dan E
- 30. Nama E(Ri) Bi ERBi Ci Zi Wi Saham 1 D 23 1,50 5,0 8,677 7,091 0,159 0,346 2 C 27 2,00 7,5 8,5 7,787 0,103 0,224 3 E 25 1,80 2,0 8,333 8,114 0,197 0,429 Total 1,000 i Nilai Zi di tabel dihitung berdasarkan rumus 5.b, sebagai berikut: Z1=(1,50/5,0)(8,677 8,114) = 0,159 Z2=(2,00/7,5)(8,5 8,114) = 0,103 Z3=(1,80/20)(8,333 8,114) = 0,197 Besarnya nilai 裡 Zj adalah sebesar Z1 + Z2 + Z3 atau 0,159 + 0,103 + 0.197=0,459. Nilai wi merupakan proporsi sekuritas ke-i. dapat dihitung berdasarkan rumus 5.a W1 = 0,159/0,459 = 0,346 = 34,6% W2 = 0,103/0,459 = 0,225 = 22,5% W3 = 0,197/0,459 = 0,429 = 42,9%