Model Lookback Presentation
- 1. Lookback analysis of exploration assessments covering the five year period from 1973 to 1977 Prepared for Hubris Enterprises inc. by Graeme Keith, Stochastic ApS
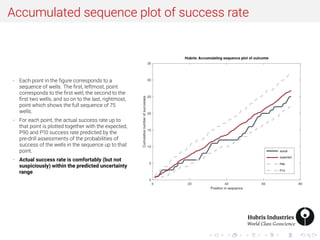
- 2. Accumulated sequence plot of success rate - Each point in the figure corresponds to a sequence of wells. The first, leftmost, point corresponds to the first well, the second to the first two wells, and so on to the last, rightmost, point which shows the full sequence of 75 wells. - For each point, the actual success rate up to that point is plotted together with the expected, P90 and P10 success rate predicted by the pre-drill assessments of the probabilities of success of the wells in the sequence up to that point. - Actual success rate is comfortably (but not suspiciously) within the predicted uncertainty range
- 3. Sliding window plot of success rate - Each point in the figure corresponds to a sequence of 25 wells. The first, leftmost, point corresponds to wells 1 to 25 in the sequence, the second to wells 2 to 26. The last, rightmost, point corresponds to wells 51 to 75. - For each window, the actual success rate for the wells in that windown is plotted together with the expected, P90 and P10 success rate predicted by the pre-drill assessments of the probabilities of success of the wells in the window. - The constant sequence length in the sliding window plot gives a clearer, less ambiguous picture of the evolution of the fidelity of predictions over time (later points uncontaminated by early statistical aberrations) - Actual success rate is comfortably within the uncertainty range and the uncertainty range corresponds well to the actual sequence variability.
- 4. Probability plot for success rate - The full sequence is divided into five groups based on assessed pre-drill probability of success: 0 to 20%, 20% to 40%, 40% to 60%, 60% to 80% and 80% to 100% - Actual success rates are shown as columns together with the expected, P90 and P10 success rates predicted by pre-drill assessments of the prospects in the interval. - The plot is designed to reveal polarization - the tendency to overestimate the significance of evidence and assess probabilities too high or too low - and the converse baselining - a tendency not to move probabilities far enough on the basis of evidence. - Polarization leads to over-prediction in the lower intervals and under-prediction in the upper intervals. - Baselining leads to under-prediction in the lower intervals and over-prediction in the upper intervals. - The plot is inconclusive. The pattern of deviation is inconsistent. - Actuals are broadly in line with predictions, except for the middle interval. However, the probability that all four intervals lie in the 80% confidence interval is only 41%, so it is not unusual to see an outlier.
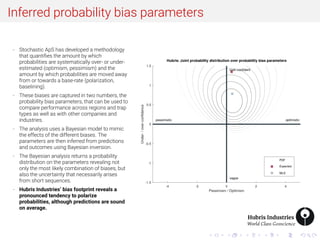
- 5. Inferred probability bias parameters - Stochastic ApS has developed a methodology that quantifies the amount by which probabilities are systematically over- or under- estimated (optimism, pessimism) and the amount by which probabilities are moved away from or towards a base-rate (polarization, baselining). - These biases are captured in two numbers, the probability bias parameters, that can be used to compare performance across regions and trap types as well as with other companies and industries. - The analysis uses a Bayesian model to mimic the effects of the different biases. The parameters are then inferred from predictions and outcomes using Bayesian inversion. - The Bayesian analysis returns a probability distribution on the parameters revealing not only the most likely combination of biases, but also the uncertainty that necessarily arises from short sequences. - Hubris Industries’ bias footprint reveals a pronounced tendency to polarize probabilities, although predictions are sound on average.
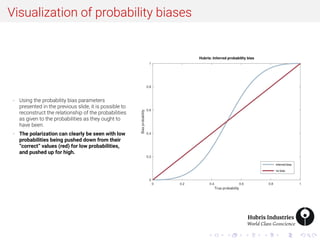
- 6. Visualization of probability biases - Using the probability bias parameters presented in the previous slide, it is possible to reconstruct the relationship of the probabilities as given to the probabilities as they ought to have been. - The polarization can clearly be seen with low probabilities being pushed down from their ”correct” values (red) for low probabilities, and pushed up for high.
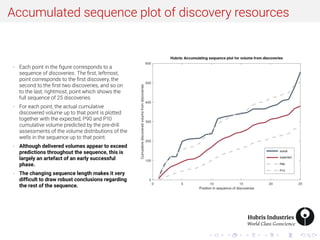
- 7. Accumulated sequence plot of discovery resources - Each point in the figure corresponds to a sequence of discoveries. The first, leftmost, point corresponds to the first discovery, the second to the first two discoveries, and so on to the last, rightmost, point which shows the full sequence of 25 discoveries. - For each point, the actual cumulative discovered volume up to that point is plotted together with the expected, P90 and P10 cumulative volume predicted by the pre-drill assessments of the volume distributions of the wells in the sequence up to that point. - Although delivered volumes appear to exceed predictions throughout the sequence, this is largely an artefact of an early successful phase. - The changing sequence length makes it very difficult to draw robust conclusions regarding the rest of the sequence.
- 8. Sliding window plot of discovery resources - Each point in the figure corresponds to a sequence of 15 discoveries. The first, leftmost, point corresponds to wells 1 to 15 in the sequence, the second to wells 2 to 16. The last, rightmost, point corresponds to wells 16 to 25. - For each window, the actual average volume per discovery in that windown is plotted together with the expected, P90 and P10 volume per discovery predicted by the pre-drill assessments of the volume distributions of the wells in the window. - The constant sequence length in the sliding window plot gives a clearer, less ambiguous picture of the evolution of the fidelity of predictions over time (later points uncontaminated by early statistical aberrations) - The early success phase is much more clearly seen. Nonetheless, delivered volumes lie comfortably in the uncertainty range throughout the sequence.
- 9. Percentile plot - Discoveries are split into ranges according to the distribution percentile corresponding to the discovered volume - The proportion of the total number of discoveries that fall into each group is plotted in the percentile plot. - The distribution of percentiles is uniform so we should expect to see roughly 20% of discoveries falling in each percentile interval - However, there will be a considerable amount of statistical variance around this 20% value, as shown the uncertainty range, which is a function of the number of discoveries. - The plot is designed to reveal over-confidence - a tendency to predict ranges that are too small - and vagueness - a tendency to predict unecessarily large uncertainty ranges. - Over-confidence leads to a higher proportion of discoveries landing in the lowest and highest percentile intervals. - Vagueness leads to a higher proportion of discoveries landing in the middle percentile intervals. - The plot is inconclusive. The pattern of deviation is inconsistent. - Actuals are broadly in line with predictions. The probability that all four intervals lie in the 80% confidence interval is only 41%, so it is not unusual to see this pattern of outliers.
- 10. Resource uncertainty bias parameters - Stochastic ApS has developed a methodology that quantifies the amount by which probability distributions are systematically over- or under-estimated (optimism, pessimism) and the amount by which ranges are over- or under-estimated (over-confidence, vagueness). - These biases are captured in two numbers, the volume bias parameters, that can be used to compare performance across regions and trap types as well as with other companies and industries. - The analysis uses a Bayesian model to mimic the effects of the different biases. The parameters are then inferred from predictions and outcomes using Bayesian inversion. - The Bayesian analysis returns a probability distribution on the parameters revealing not only the most likely combination of biases, but also the uncertainty that necessarily arises from short sequences. - Hubris Industries’ volume bias footprint also reveals a pronounced tendency to over-confidence, although predictions are sound on average.
- 11. Empirical distribution plot - An alternative way to illustrate the deviation from uniformity of the prediction of percentiles is by plotting the actual attained percentiles in an ordered list from least to greatest. - Theory predicts that - as always, within a certain range of uncertainty - these percentiles should fall on a straight line according to their uniform distribution. - The empirical distribution of percentiles can also be predicted based on the resource bias parameters presented in the previous slide. - The plot reveals both optimism and pessimism, as well as over-confidence and vagueness. - Optimism leads to percentiles that are consistently under the no-bias curve. Pessimism, conversely, leads to an upward lift on the empirical curve - Over-confidence leads to a steepening of the curve as prospects come in with unexpectedly low and high percentiles. - Conversely vagueness leads to a flattening of the curve, as everything comes in around the middle of the wide ranges - Both the empirical distribution and the predicted distribution based on the bias parameters show a tendency to underestimate uncertainty.