Modul 2 : Persamaan linear
- 1. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 20 tc_fatimah@KVSandakan UNIT 2.0 : PERSAMAAN LINEAR Objektif Am : Mempelajari serta mengetahui cara-cara menyelesaikan persamaan linear menggunakan kaedah-kaedah tertentu. Objektif Khusus : 2.1.1 Menulis persamaan linear dalam satu pemboleh ubah bagi pernyataan yang diberi dan begitu juga sebaliknya. 2.1.2 Menyelesaikan persamaan linear dalam satu pemboleh ubah. 2.1.3 Menyelesaikan masalah yang melibatkan persamaan linear dalam satu pemboleh ubah. 2.2.1 Menulis persamaan linear dalam dua pemboleh ubah bagi pernyataan yang diberi. 2.2.2 Menentukan nilai satu pemboleh ubah apabila diberi nilai pemboleh ubah yang lain. 2.2.3 Menentu dan menjelaskan penyelesaian yang mungkin bagi persamaan linear dalam dua pemboleh ubah. 2.3.1 Membentuk persamaan linear serentak berdasarkan situasi harian. 2.3.2 Menyelesaikan persamaan linear serentak dalam dua pemboleh ubah menggunakan pelbagai kaedah. 2.3.3 Menyelesaikan masalah yang melibatkan persamaan linear serentak dalam dua pemboleh ubah.
- 2. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 21 tc_fatimah@KVSandakan 2.1 PERSAMAAN LINEAR DALAM SATU PEMBOLEH UBAH Contoh INGAT SEMULA Sebutan algebra linear ¨C sebutan dengan pemboleh ubah yang mempunyai kuasa 1. 2m, ¨C 2c, 1 2 ? Ungkapan algebra linear ¨C gabungan satu atau lebih sebutan linear yang dihubungkan oleh operasi penambahan atau penolakan atau kedua-duanya. 2x ¨C 5y, 4x + 6y, 3p ¨C 6q + 4r 1. Tentukan sama ada persamaan berikut adalah sebutan algebra linear. Tandakan (¡Ì ) atau ( ¡Á ). (a) 6y2 ( ) (b) 7a2 ( ) (c) ¨C 7m ( ) (d) 7? 10 ( ) (e) 3pq ( ) 2. Tentukan sama ada ungkapan berikut adalah ungkapan algebra linear. Tandakan (¡Ì ) atau (¡Á). (a) 5s ¨C p3 ( ) (b) 1 2 h ¨C 4p ( ) (c) 3q + 8r ( ) (d) ¨C 3g ( ) (e) 4y + x ( ) 3. Tentukan sama ada persamaan berikut adalah persamaan linear. Tandakan (¡Ì ) atau ( ¡Á ). (a) 2y + 3 = 7 ( ) (b) 7? 10 ¨C 10 = 10 ( ) (c) q2 + r = 4 ( ) (d) ¨C 3g = 9 ( ) 4. Tandakan (¡Ì ) pada suatu persamaan linear dalam satu pemboleh ubah. (a) m + 5 = 12 ( ) (b) 2p ¨C k = 14 ( ) (c) p + q = 20 ( ) (d) y ¨C 10 = 3 ( ) REVISI 1
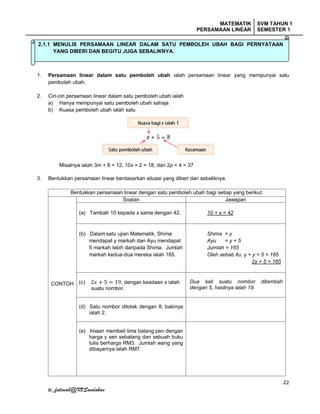
- 3. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 22 tc_fatimah@KVSandakan 1. Persamaan linear dalam satu pemboleh ubah ialah persamaan linear yang mempunyai satu pemboleh ubah. 2. Ciri-ciri persamaan linear dalam satu pemboleh ubah ialah a) Hanya mempunyai satu pemboleh ubah sahaja b) Kuasa pemboleh ubah ialah satu Misalnya ialah 3m + 8 = 12, 10x + 2 = 18, dan 2p + 4 = 37 3. Bentukkan persamaan linear berdasarkan situasi yang diberi dan sebaliknya. Bentukkan persamaan linear dengan satu pemboleh ubah bagi setiap yang berikut. CONTOH Soalan Jawapan (a) Tambah 10 kepada x sama dengan 42. 10 + x = 42 (b) Dalam satu ujian Matematik, Shima mendapat y markah dan Ayu mendapat 5 markah lebih daripada Shima. Jumlah markah kedua-dua mereka ialah 165. Shima = y Ayu = y + 5 Jumlah = 165 Oleh sebab itu, y + y + 5 = 165 2y + 5 = 165 (c) 2? + 5 = 19, dengan keadaan x ialah suatu nombor. Dua kali suatu nombor ditambah dengan 5, hasilnya ialah 19. (d) Satu nombor ditolak dengan 8, bakinya ialah 2. (e) Imaan membeli lima batang pen dengan harga y sen sebatang dan sebuah buku tulis berharga RM3. Jumlah wang yang dibayarnya ialah RM7. 2.1.1 MENULIS PERSAMAAN LINEAR DALAM SATU PEMBOLEH UBAH BAGI PERNYATAAN YANG DIBERI DAN BEGITU JUGA SEBALIKNYA.
- 4. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 23 tc_fatimah@KVSandakan 1. Bentukkan persamaan linear dalam satu pemboleh ubah bagi setiap yang berikut. a) ? ? 2 = 8 dengan keadaan y ialah umur Wati sekarang. Jawapan : b) Hasil bahagi suatu nombor dengan 6 ialah 12. Jawapan : c) Harga sekilogram ayam ialah RMy, Laila membeli 5 kg ayam dengan jumlah bayaran RM40. Jawapan : d) Perimeter sebuah segi empat tepat dengan panjang 2? m dan lebar 5 m ialah 14 m. Jawapan : 2. Tulis pernyataan atau situasi bagi setiap persamaan yang berikut. 1. ? ? 1 = 6 dengan keadaan ? ialah suatu nombor. Jawapan : 2. ? + 10 = 78 dengan keadaan ? ialah markah ujian Yummy. Jawapan : 3. 4? = 50 dengan keadaan ? ialah jisim sebungkus beras, dalam kg. Jawapan : LATIHAN 1
- 5. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 24 tc_fatimah@KVSandakan 1. Persamaan linear dalam satu pemboleh ubah boleh diselesaikan dengan menggunakan tiga kaedah yang berikut. a) Kaedah cuba jaya b) Kaedah kesamaan c) Kaedah pematahbalikan Selesaikan persamaan linear 2? + 1 = 7 dengan memuaskan. Penyelesaian (a) Kaedah cuba jaya Nilai ? Sebelah kiri = 2? + 1 Semakan Refleksi 1 2 ( 1 ) +1 = ____ 2 2 ( 2 ) +1 = ____ 3 2 ( 3 ) +1 = ____ Maka x = _______________ (b) Kaedah kesamaan 2? + 1 = 7 2? = 7 ? 1 2? = 6 ? = ___________ 2.1.2 MENYELESAIKAN PERSAMAAN LINEAR DALAM SATU PEMBOLEH UBAH. CONTOH 1
- 6. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 25 tc_fatimah@KVSandakan (c) Kaedah pematahbalikan Maka x = _______________ Contoh dan penyelesaian Menyelesaikan persamaan dalam bentuk: Bentuk Contoh x + a = b x + 2 = 6 ? x = 6 ¨C 2 = 4 x ¨C a = b x ¨C 3 = 4 ? x = 4 + 3 = 7 ax = b 4x = 12 ? x = 4 12 = 3 0, ?? ab a x 2 x = 6 ? x = 6 ? 2 = 12 Menyelesaikan persamaan dalam bentuk ax + b = c, apabila a,b, c ialah integer dan x ialah pemboleh ubah. Selesaikan 2x + 4 = 8 2x = 8 ¨C 4 x = 2 4 x = 2 Selesaikan 3x ¨C 6 = 9 Penyelesaian masalah (a) 5x ¨C 4 = 4 + x 5x ¨C x = 4 + 4 4x = 8 x = 2 (b) 3 4 x + 3 = 6 3 4 x = 6 ¨C 3 3x = 12 x = 4 CONTOH 2
- 7. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 26 tc_fatimah@KVSandakan 1 Selesaikan persamaan linear berikut: (a) x + 3 = 9 (b) 4x = 16 (c) x + 9 = 4 (d) 2x = 18 (e) x ? 5 = 3 (f) 6 y = 4 (g) x ?10 = 4 (h) 2 m = ?12 2 Selesaikan persamaan linear berikut: (a) 3x + 4 = 28 (b) 5x + 7 = 32 (c) 6m ? 5 = 49 (d) 9k ?11 = ?38 3 Selesaikan persamaan linear berikut: (a) 14 ? 3x = 5 ? 6x (b) 2(2x ? 5) = 14 LATIHAN 2
- 8. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 27 tc_fatimah@KVSandakan (c) 5x + 24 = ?3x (d) 3(2x ? 3) + 5(3 ? x) = 4 (e) 2??2 3 = 3?+5 4 (f) ??2 5 = 2 ¨C c Selepas 10 tahun, umur Ain akan menjadi tiga kali umurnya sekarang. Berapakah umur Ain? Penyelesaian Langkah 1 : Memahami masalah Langkah 2 : Merancang strategi Langkah 3 : Melaksanakan strategi Langkah 4 : Membuat refleksi 2.1.3 MENYELESAIKAN MASALAH YANG MELIBATKAN PERSAMAAN LINEAR DALAM SATU PEMBOLEH UBAH. CONTOH Selepas 10 tahun, umur Ain akan menjadi tiga kali umurnya sekarang Katakan umur Ain sekarang = ? Selepas 10 tahun, umur Ain = 3 ¡Á ? = 3? Persamaan linear dalam satu pemboleh ubah yang dibentuk ialah ? + 10 = 3? ? + 10 = 3?
- 9. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 28 tc_fatimah@KVSandakan Bil Soalan 1 Dalam satu ujian matematik, Rina memperoleh 17 markah lebih daripada Aiman manakala markah Izzah adalah dua kali ganda markah Aiman. Sekiranya jumlah markah ketiga-tiga orang murid itu ialah 161, berapakah markah Rina? 2 Rajah dibawah menunjukkan sebuah segi empat tepat. Jika perimeter segi empat tepat itu ialah 66 cm, berapakah luas segi empat tepat itu? 3 Rajah menunjukkan dua buah silinder yang sama. Silinder ? diisi dengan air sehingga separuh penuh. Hitung nilai ?. 7? + 18 5? Silinder ?Silinder ? LATIHAN 3 (2? + 1)?? (? + 5)??
- 10. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 29 tc_fatimah@KVSandakan Bil Soalan 4 Sebuah segi empat tepat berukuran (5 ? 6?) cm panjang dan ( ? + 4) cm lebar. Jika perimeter segi empat tepat tersebut ialah 20 cm, hitung panjang, dalam cm. 5 Sebuah syarikat menjual sebuah televisyen pada harga (1.5? + 70) di mana ? ialah harga kos. Jika harga jualan bagi televisyen tersebut ialah RM2 500, hitung keuntungan yang diperoleh.
- 11. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 30 tc_fatimah@KVSandakan 2.2 PERSAMAAN LINEAR DALAM DUA PEMBOLEH UBAH INGAT SEMULA 1. Persamaan linear dalam dua pemboleh ubah ialah persamaan linear yang mempunyai dua pemboleh ubah. 2. Ciri-ciri persamaan linear dalam dua pemboleh ubah ialah a) Mempunyai dua pemboleh ubah b) Kuasa bagi setiap pemboleh ubah ialah satu 3. Bentuk am persamaan linear dalam dua pemboleh ubah dengan keadaan ? dan ? bukan sifar Misalnya, 6? + 4? = 9, dan 5? + 2? = 8 1. Antara persamaan linear dalam dua pemboleh ubah berikut, yang manakah ditulis dalam bentuk am? Bulatkan jawapan anda. 2. Tentukan sama ada persamaan yang berikut ialah persamaan linear dalam dua pemboleh ubah atau bukan. a) 3? ? ? = 6 b) 7?2 + 5? = 9 c) 2(? + 8) = 5? d) ? 6 + 4 = ?2? Jawapan a) b) c) d) ?? + ?? = ? REVISI 2
- 12. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 31 tc_fatimah@KVSandakan Bentukkan persamaan linear dalam dua pemboleh ubah bagi setiap yang berikut. (a) Beza antara dua nombor ialah 18. (b) Simpanan wang saku Ahmad ialah RM? dan simpanan wang saku Norita ialah RM?. Jumlah simpanan wang mereka ialah RM600. (c) Sebuah bas dan sebuah van masing-masing dapat membawa ? dan ? orang penumpang. Jumlah penumpang yang dibawa oleh dua buah bas dan lima buah van ialah 100 orang. Penyelesaian (a) Katakan dua nombor itu masing-masing ialah ? dan ?. ? ? ? = 18 (b) Jumlah simpanan = 600 ? + ? = 600 (c) Jumlah penumpang =100 2? + 5? = 100 Bentukkan persamaan linear dalam dua pemboleh ubah bagi setiap yang berikut. Bil Soalan Penyelesaian 1 Dalam satu acara lompat jauh, jumlah mata yang diperoleh rumah sukan Satria dan rumah sukan Perdana ialah 258. 2 Sebuah segi empat tepat dengan perimeter 140 cm mempunyai ( ? + 1) cm panjang dan ( ? ? 2) cm lebar. 3 Jumlah harga tiket bagi suatu taman tema air untuk lapan orang dewasa dan lima orang kanak-kanak ialah RM265. 4 Aminah menjual nasi lemak dan mi goreng setiap pagi. Pada suatu hari, dia telah menjual 145 bungkus. 5 Safi membeli ? kotak susu dan ? botol air mineral. Harga sekotak susu ialah RM5.50 dan sebotol air minuman ialah RM2.60. Dia membayar RM70.30 untuk kesemua barang yang dibelinya. 2.2.1 MENULIS PERSAMAAN LINEAR DALAM DUA PEMBOLEH UBAH BAGI PERNYATAAN YANG DIBERI. CONTOH LATIHAN 4
- 13. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 32 tc_fatimah@KVSandakan Diberi bahawa 5x + 2y = 8, cari nilai bagi (a) y, jika x = 3 (b) x, jika y = ¨C 6 Penyelesaian (a) Langkah 1 Gantikan nilai x = 3, dalam persamaan 5x + 2y = 8 5(3) + 2y = 8 Langkah 2 Selesaikan 2y = 8 ¨C 15 ? = 7 2 (b) Bagi setiap persamaan linear yang berikut, cari nilai y apabila x diberikan dan sebaliknya. Bil Soalan 1 (a) 2x + 5y = 10, (i) cari nilai y apabila x = 2. (ii) cari nilai x, apabila y = 3. 2.2.2 MENENTUKAN NILAI SATU PEMBOLEH UBAH APABILA DIBERI NILAI PEMBOLEH UBAH YANG LAIN. CONTOH LATIHAN 5
- 14. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 33 tc_fatimah@KVSandakan Bagi setiap persamaan linear yang berikut, cari nilai y apabila x diberikan dan sebaliknya. Bil Soalan 1 (b) y = 8 3 5 ?x (i) cari nilai y apabila x = 3. (ii) cari nilai x, apabila y = 2. (c) ? 3 y 1 4 ? x (i) cari nilai y apabila x = 8. (ii) cari nilai x, apabila y = ?3. 2 Diberi bahawa 2? = ?11 + 10?. Cari nilai a) x apabila y = 2, b) y apabila x = 5. 3 Diberi bahawa 32 = 4? ? 2?. Cari nilai a) x apabila y = 4, b) y apabila x = ?4. 4 Diberi bahawa ?4? + 2? = 18. Cari nilai a) x apabila y = 3, b) y apabila x = 2
- 15. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 34 tc_fatimah@KVSandakan Tentukan sama ada persamaan berikut adalah persamaan linear serentak. (a) 3x ¨C 2y = 6 dan 4x ¨C 3y = 7 Ya. (b) 5x + 2y = 8 dan 3x ¨C 2b = 6 Bukan. 1. Diberi x dan y ialah integer. Cari dua penyelesaian yang mungkin bagi persamaan linear berikut. Bil Soalan contoh ?2? + 6? = 32 Penyelesaian Gantikan sebarang nilai x yang sesuai ke dalam persamaan. Jika ? = ?1, maka ?2(?1) + 6? = 32 2 + 6? = 32 6? = 30 ? = 5 2.2.3 MENENTU DAN MENJELASKAN PENYELESAIAN YANG MUNGKIN BAGI PERSAMAAN LINEAR DALAM DUA PEMBOLEH UBAH. CONTOH LATIHAN 6
- 16. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 35 tc_fatimah@KVSandakan 1 12? = 6? ? 60 2 4? + 56 = 6? 3 36? + 12 = ?2?
- 17. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 36 tc_fatimah@KVSandakan 2.3 PERSAMAAN LINEAR SERENTAK INGAT SEMULA 1. Persamaan linear serentak dalam dua pemboleh ubah ialah dua persamaan linear yang mempunyai dua pemboleh ubah yang sama serta mempunyai penyelesaian sepunya. Contoh: ? + ? = 10 4? + 5? = 20 1. Tentukan jika pasangan berikut ialah persamaan serentak dalam dua pemboleh ubah. Bil Persamaan Linear Ya / Tidak 1 ? ? 2? = 8 ?4? + 6? = 12 2 4? ? 3? = 9 6? + ? = ?5 3 2?? ? 8? = 3 ? ? ? = ?12 4 ? = 6? ? + 12 = ?42 2. Bentukkan persamaan linear serentak berdasarkan situasi berikut. (a) Mawaddah dan Farhana berkongsi 50 biji gula-gula. Mawaddah mendapat 4 biji gula-gula lebih daripada Farhana, (b) Hasil tambah umur bagi dua orang adik beradik ialah 30 tahun dan beza umur mereka ialah 6 tahun. 2.3.1 MEMBENTUK PERSAMAAN LINEAR SERENTAK BERDASARKAN SITUASI HARIAN. Persamaan 1 Kedua-dua persamaan mempunyai pemboleh ubah yang sama iaitu ? dan ?.Persamaan 2 REVISI 3
- 18. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 37 tc_fatimah@KVSandakan CONTOH Selesaikan persamaan linear serentak dengan menggunakan kaedah berikut. a) Kaedah Penggantian 2x + y = 3 ............. 3x ¨C 2y = 8 ........... Daripada y = 3 ¨C 2x ........... Gantikan ke dalam 3? ¨C 2 ( 3 ¨C 2? ) = 8 3? ¨C 6 + 4? = 8 7? = 14 ? = 2 Gantikan x = 2 ke dalam ? = 3 ¨C 2 ( 2) ? = 3 ¨C 4 ? = ¨C 1 Maka, x = 2 dan y = ¨C 1. b) Kaedah Penghapusan 2x + y = 3 ......... 3x ¨C 2y = 8 .......... ¡Á 2 4x + 2y = 6 ......... + 7x = 14 x = 2 Gantikan x = 2 ke dalam 2 ( 2 ) + y = 3 y = 3 ¨C 4 y = ¨C 1 Maka, x = 2 dan y = ¨C 1. 2.3.2 MENYELESAIKAN PERSAMAAN LINEAR SERENTAK DALAM DUA PEMBOLEH UBAH MENGGUNAKAN PELBAGAI KAEDAH. 1 2 1 3 3 2 3 1 1 2 1 3 2 3 Ungkapkan x dalam sebutan y Kenal pasti pemboleh ubah dengan pekali yang sama
- 19. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 38 tc_fatimah@KVSandakan Carikan nilai bagi x dan y bagi persamaan linear serentak berikut. 1. 5? ? 3? = 13 2? + 3? = 1 2. 3? ? 4? = 13 ? ? 3? = 4 3. 3? + 7? = 2 2? ? 9? = 15 LATIHAN 7
- 20. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 39 tc_fatimah@KVSandakan CONTOH Penyelesaian masalah Hasil tambah umur bagi dua orang adik beradik ialah 30 tahun dan beza umur mereka ialah 6 tahun. Cari umur mereka. Katakan umur mereka ialah x tahun dan y tahun. x + y = 30 ............. x ¨C y = 6 ............. 2x = 36 x = 18 Gantikan x = 18 ke dalam x + y = 30, 18 + y = 30 y = 30 ¨C 18 y = 12 Umur mereka ialah 18 tahun dan 12 tahun. 1 Selesaikan persamaan linear serentak berikut. a) 2x + y = 7 3x ¨C 5y = 30 b) 5d ¨C 2e = 16 d + 4e = ?10 1 2 + 2.3.3 MENYELESAIKAN MASALAH YANG MELIBATKAN PERSAMAAN LINEAR SERENTAK DALAM DUA PEMBOLEH UBAH. LATIHAN 8
- 21. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 40 tc_fatimah@KVSandakan 1 Selesaikan persamaan linear serentak berikut. c) 3 5 3 1 m n m n ? ? ? ? ? d) 3 4 16 2 8 k n k n ? ? ? ? ? e) 11 2 3 2 x y x y ? ? ? ? f) 4 2 2 3 8 m n m n ? ? ? ?
- 22. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 41 tc_fatimah@KVSandakan 2 Selesaikan persamaan linear berikut. a) 3? ? 4? = 13 ? ? 3? = ?4 b) 5? ? 3? = 13 2? + 3? = 1 c) 3? + 7? = 2 2? ? 9? = 15 d) 2? ? ? = 1 4? + 2? = 14
- 23. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 42 tc_fatimah@KVSandakan 3 Selesaikan masalah berikut a) Mawaddah dan Farhana berkongsi 50 biji gula-gula. Jika Mawaddah mendapat 4 biji gula- gula lebih daripada Farhana, cari bilangan gula-gula yang diperoleh bagi setiap orang. b) Luqman dan Ali membeli 10 biji epal dan 6 biji oren dengan harga RM21. Nashrullah membeli 5 biji epal dan 8 biji oren dengan harga RM18. Cari harga bagi sebiji epal dan sebiji oren. c) Rajah di atas menunjukkan satu segi empat selari PQRS. Cari nilai x dan y. S R QP 11 cm 7 cm ( 2x + y ) cm ( 4x + y ) cm
- 24. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 43 tc_fatimah@KVSandakan 4 Umur Puan Aishah ialah 3 kali ganda umur anaknya. Dalam masa 4 tahun lagi, jumlah umur kedua-duanya ialah 68 tahun. Cari umur Puan Aishah sekarang. 5 Dalam sebuah kotak terdapat 24 botol minuman berperisa epal dan anggur. Harga sebotol minuman berperisa epal ialah RM3.00 dan harga sebotol minuman berperisa anggur ialah RM2.00. Jika harga bagi kotak itu ialah RM58.00, berapakah bilangan botol minuman berperisa epal? 6 Sebuah pusat tuisyen mengenakan yuran pendaftaran sebayak RM50 bagi seorang pelajar. Yuran yang dikenakan bagi satu mata pelajaran wajib ialah RM25 dan RM15 bagi mata pelajaran elektif. Danial mendaftar di pusat tuisyen itu dan mengambil 6 mata pelajaran wajib kesemuanya. Jika jumlah bayaran yang dibayar oleh Danial ialah RM180, berapakah bilangan mata pelajaran wajib yang diambilya?
- 25. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 44 tc_fatimah@KVSandakan CONTOH SOALAN PEPERIKSAAN 1. Selesaikan tiap-tiap persamaan berikut: a) 2? = 8 [ 1 markah ] b) ?+2 5 = 3 [ 2 markah ] 2. a) Rajah menunjukkan empat persamaan linear yang diberikan oleh pelajar A. Rajah 2 Nyatakan dua persamaan linear dalam satu pemboleh ubah daripada persamaan yang diberikan oleh pelajar A. [ 2 markah ] b) Selesaikan persamaan linear berikut. ? 3 = ?4 [ 1 markah ] 3. a) Perimeter sebuah ladang kelapa sawit berbentuk segi empat tepat ialah 1600 m. Panjang dan lebar ladang itu diwakili oleh ? dan ? masing-masing. Tulis satu persamaan linear dengan dua pemboleh ubah bagi situasi di atas. [ 2 markah ] b) Sebuah syarikat membayar gaji seorang pekerja mahir, ?, RM40 sehari dan seorang pekerja tidak mahir, ?, RM25 sehari. Terdapat 15 orang pekerja dan jumlah gaji harian mereka ialah RM450. Cari bilangan pekerja mahir ( ?) dan bilangan pekerja tidak mahir ( ?). [ 5 markah ] ? ? 28 = 0 2 ? + 3? = 12 7? + 6 = 18 2?2 + 8 = 3
- 26. MATEMATIK PERSAMAAN LINEAR SVM TAHUN 1 SEMESTER 1 45 tc_fatimah@KVSandakan 4. a) Rajah 2 menunjukkan maklumat bagi dua orang pelajar lelaki Rajah 2 Diberi jumlah tinggi kedua-dua pelajar ialah 294 cm manakala jumlah jisim mereka pula ialah 126kg. (a) Tulis dua persamaan linear serentak dari maklumat di atas. [ 2 markah ] (b) Hitungkan nilai kedua-dua pemboleh ubah. [ 4 markah ]
























![MATEMATIK
PERSAMAAN LINEAR
SVM TAHUN 1
SEMESTER 1
44
tc_fatimah@KVSandakan
CONTOH SOALAN PEPERIKSAAN
1. Selesaikan tiap-tiap persamaan berikut:
a) 2? = 8 [ 1 markah ] b)
?+2
5
= 3 [ 2 markah ]
2. a) Rajah menunjukkan empat persamaan linear yang diberikan oleh pelajar A.
Rajah 2
Nyatakan dua persamaan linear dalam satu pemboleh ubah daripada persamaan yang diberikan
oleh pelajar A.
[ 2 markah ]
b) Selesaikan persamaan linear berikut.
?
3
= ?4
[ 1 markah ]
3. a) Perimeter sebuah ladang kelapa sawit berbentuk segi empat tepat ialah 1600 m. Panjang dan lebar
ladang itu diwakili oleh ? dan ? masing-masing.
Tulis satu persamaan linear dengan dua pemboleh ubah bagi situasi di atas.
[ 2 markah ]
b) Sebuah syarikat membayar gaji seorang pekerja mahir, ?, RM40 sehari dan seorang pekerja tidak
mahir, ?, RM25 sehari. Terdapat 15 orang pekerja dan jumlah gaji harian mereka ialah RM450.
Cari bilangan pekerja mahir ( ?) dan bilangan pekerja tidak mahir ( ?).
[ 5 markah ]
? ? 28 = 0
2
?
+ 3? = 12
7? + 6 = 18 2?2
+ 8 = 3](https://image.slidesharecdn.com/modul2persamaanlinear-201106134747/85/Modul-2-Persamaan-linear-25-320.jpg)
![MATEMATIK
PERSAMAAN LINEAR
SVM TAHUN 1
SEMESTER 1
45
tc_fatimah@KVSandakan
4. a) Rajah 2 menunjukkan maklumat bagi dua orang pelajar lelaki
Rajah 2
Diberi jumlah tinggi kedua-dua pelajar ialah 294 cm manakala jumlah jisim mereka pula ialah 126kg.
(a) Tulis dua persamaan linear serentak dari maklumat di atas.
[ 2 markah ]
(b) Hitungkan nilai kedua-dua pemboleh ubah.
[ 4 markah ]](https://image.slidesharecdn.com/modul2persamaanlinear-201106134747/85/Modul-2-Persamaan-linear-26-320.jpg)