Modul 6 spl
Download as pptx, pdf7 likes13,981 views
Dokumen ini membahas sistem persamaan linier (SPL) yang merupakan persamaan matematika dengan n variabel dan m persamaan. Metode penyelesaian SPL dijelaskan, termasuk klasifikasi menjadi homogen dan non-homogen, serta penggunaan metode eliminasi untuk menemukan solusi. Konsistensi sistem ditentukan melalui rank matriks, dengan contoh-contoh untuk menggambarkan kondisi solusi yang konsisten dan tidak konsisten.
![METODE ELIMINASI GOUSS
Andaikan diberikan SPL dengan
m persamaan linier dan n variabel
yang tidak diketahui, x1, x2,,xn
yaitu :
AX = B
Langkah-langkah menentukan
konsitensi dan solusi SPL non
homogen adalah sbb :
(1). Bentuk matrik lengkap [A,B]
(2). Reduksilah matrik lengkap
[AB] menjadi matrik eselon
baris tereduksi, E[AB] dengan
menggunakan serangkaian
operasi elementer baris
(3). Dari E[AB], hitunglah rank
matrik, r(A) dan r(AB), dengan
cara menghitung jumlah baris
tak nolnya.
(4). Konsistensi SPL
(a). Jika r(A)=r(AB)=n, maka SPL
konsisten solusi tunggal
(b). Jika r(A)=r(AB)=r < n, maka
SPL konsisten solusi memuat
parameter
(c). Jika r(A)r(AB), maka SPL
tidak konsisten/tidak ada
solusi
(5). Solusi SPL
(a). Jika SPL konsisten, susunan
SPL dari matrik eselon
(b). Tentukan solusi SPL dengan
cara eliminasi berulang dari xn
ke x1](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-9-320.jpg)
![CONTOH : TIDAK KONSISTEN
Tentukanlah solusi SPL jika ada
Jawab
Matrik lengkap SPL :
Operasi elementer baris
Reduksi x1
1053
832
522
221
321
321
緒
緒
緒
xxx
xxx
xxx
10531
8132
5221
],[ BA
`
5310
2310
5221
H2 H2 2H1
H3 H3 1 H1
Reduksi x2
Jadi,
Analisis
(1). Jumlah baris tak nol A = 2,
sehingga r(A) = 2
(2). Jumlah baris tak nol [A,B]=3,
sehingga, r(A,B)=3
(3). Karena r(A)r(A,B), maka SPL
tidak konsisten, atau SPL tidak
ada solusi
`
3000
2310
5221
H3 H3+H2
`
3000
2310
5221
],[
BAE](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-10-320.jpg)
![CONTOH : SOLUSI PARAMETER
Tentukanlah solusi SPL jika ada
Jawab
Matrik lengkap SPL :
142486
7243
24274
26242
4321
4321
4321
4321
緒
緒
緒
緒
xxxx
xxxx
xxxx
xxxx
142486
71243
24274
26242
],[ BA
Reduksi x1
1 2 -1 3 -1 H1=(1/a11)H1
0 -1 2 -8 6 H2=H2-(a21/a11)H1
0 -2 5 -10 10 H3=H3-(a31/a11)H1
0 -4 10 -20 20 H4=H4-(a41/a11)H1
Reduksi x2
1 2 -1 3 -1
0 1 -2 8 -6 H2=(1/a22)H2
0 0 1 6 -2 H3=H3-(a32/a22)H2
0 0 2 12 -4 H4=H4-(a42/a22)H2
Reduksi x3
1 2 -1 3 -1
0 1 -2 8 -6
0 0 1 6 -2 H3=(1/a33)H3
0 0 0 0 0 H4=H4-(a43/a33)H3](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-11-320.jpg)
![SOLUSI : SPL Parameter
00000
2-6100
6-82-10
1-31-21
),( BAE
Dari matrik eselon dperoleh hasil :
(1). Jumlah baris tak nol A=3,
sehingga r(A)=3
(2). Jumlah baris tak nol [A,B]=3,
sehingga r(A,B)=3
(3). Jumlah variabel yang tidak
diketahui x1,x2,x3,x4 = 4
(4). Jadi r(A)=r(A,B)=3<n=4, maka
SPL konsisten dan solusi
memuat (n-r=1) parameter
26
682
132
43
432
4321
緒
緒
緒
xx
xxx
xxxx
Solusi :
x4 = t, t parameter
x3 = 2 6x4
= 2 6t
x2 = 6 + 2x3 8x4
= 6 + 2( 2 6t) 8t
= 10 20t
x1 = 1 2x2 + x3 3x4
=1 2( 10 20t) + ( 2 6t) 3t
= 19 + 31t
SPL dari matrik eselon](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-12-320.jpg)
![CONTOH : SOLUSI PARAMETER
Tentukanlah solusi SPL jika ada
Jawab
Matrik lengkap SPL :
1 2 3 4 2 x1 0
2 5 4 6 5 x2 0
3 5 6 7 6 x3 0
1 2 4 7 9 x4 0
2 3 8 10 3 x5 0
0310832
017421
087673
056452
024321
],[ BA
Reduksi x1
1 2 3 4 2 0 H1=(1/a11)H1
0 1 -2 -2 1 0 H2=H2-(a21/a11)H1
0 1 -3 -5 2 0 H3=H3-(a31/a11)H1
0 0 1 3 -1 0 H4=H4-(a41/a11)H1
0 -1 2 2 -1 0 H5=H5-(a51/a11)H1
Reduksi x2
1 2 3 4 2 0
0 1 -2 -2 1 0 H2=(1/a22)H2
0 0 -1 -3 1 0 H3=H3-(a32/a22)H2
0 0 1 3 -1 0 H4=H4-(a42/a22)H2
0 0 0 0 0 0 H5=H5-(a52/a22)H2
Reduksi x3
1 2 3 4 2 0
0 1 -2 -2 1 0
0 0 1 3 -1 0 H3=(1/a33)H3
0 0 0 0 0 0 H4=H4-(a43/a33)H3
0 0 0 0 0 0 H5=H5-(a53/a33)H3](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-13-320.jpg)
![Dari matrik eselon dperoleh hasil :
(1). Jumlah baris tak nol A=3,
sehingga r(A)=3
(2). Jumlah baris tak nol [A,B]=3,
sehingga r(A,B)=3
(3). Jumlah variabel yang tidak
diketahui x1,x2,x3,x4,x5 = 5
(4). Jadi r(A)=r(A,B)=3<n=5, maka
SPL konsisten dan solusi
memuat (n-r=2) parameter
000000
000000
01-3100
012-2-10
024321
),( BAE
SOLUSI : SPL Parameter
Solusi :
x5 = s, s parameter
x4 = t, t parameter
x3 = 3x4 + x5
= 3t + s
x2 = 2x3 + 2x4 x5
= 2(3t + s) + 2t s
= 4t + s
x1 = 2x2 3x3 4x4 2x5
= 2(4t +s) 3(3t+s) 4t 2s
= 13t 7s
03
022
02432
543
5432
54321
緒
緒
緒
xxx
xxxx
xxxxx
SPL dari matrik eselon](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-14-320.jpg)
![CONTOH : SOLUSI TUNGGAL
Carilah solusi SPL jika ada
Jawab
Matrik lengkap SPL adalah :
1342
72243
28274
46242
4321
4321
4321
4321
緒
緒
緒
緒
xxxx
xxxx
xxxx
xxxx
134211
72243
24274
46242
],[ BA
Reduksi x1
1 2 -1 4 2 H1=(1/a11)H1
0 -1 2 -8 -6 H2=H2-(a21/a11)H1
0 -2 5 -10 1 H3=H3-(a31/a11)H1
0 -1 3 0 11 H4=H4-(a41/a11)H1
Reduksi x2
1 2 -1 4 2
0 1 -2 8 6 H2=(1/a22)H2
0 0 1 6 13 H3=H3-(a32/a22)H2
0 0 1 8 17 H4=H4-(a42/a22)H2
Reduksi x3
1 2 -1 4 2
0 1 -2 8 6
0 0 1 6 13 H3=(1/a33)H3
0 0 0 2 4 H4=H4-(a43/a33)H3](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-15-320.jpg)
![Reduksi x4
1 2 -1 4 2
0 1 -2 8 6
0 0 1 6 13
0 0 0 1 2 H4=(1/a44)H4
Dari matrik eselon dperoleh hasil :
(1). Jumlah baris tak nol A=4,
sehingga r(A)=4
(2). Jumlah baris tak nol [A,B]=4,
sehingga r(A,B)=4
(3). Jumlah variabel yang tidak
diketahui x1,x2,x3,x4 = 4
(4). Jadi r(A)=r(A,B)=r=4, maka
SPL konsisten dan solusi
tunggal
SPL dari matrik eselon
2
136
682
242
4
43
432
4321
緒
緒
緒
x
xx
xxx
xxxx
Solusi :
x4 = 2
x3 = 13 6(2)
= 1
x2 = 6 + 2x3 8x4
= 6 + 2(1) 8(2)
= 8
x1 = 2 2x2 + x3 4x4
= 2 2(8) + 1 4(2)
= 11](https://image.slidesharecdn.com/modul6spl-130914064051-phpapp01/85/Modul-6-spl-16-320.jpg)
Modul 6 spl
- 1. MODUL VI SISTEM PERSAMAAN LINIER (SPL) PRAYUDI
- 2. PENGERTIAN SISTEM PERSAMAAN LINIER Persamaan linier adalah suatu persamaan dengan n variabel yang tidak diketahui x1,x2,x3., xn yang dinyatakan dalam bentuk : dimana a1,a2, , an dan b adalah kontanta real (kompleks). Persamaan linier secara geometri dengan istilah garis. Contoh Persamaan linier : (1). 2x1 + 4x2 = 10 (2). 2x1 4x2 + 3x3 + 4x4 = 5 12211 ... bxaxaxa nn 緒 Secara umum, sistem persamaan linier adalah suatu susunan yang terdiri dari m persamaan linier dan n variabel yang tidak diketahui yang berbentuk : dimana x1, x2, , xn disebut variabel yang tidak diketahui, aij konstanta koefisien sistem persamaan linier dan bj konstanta yang diketahui mnmnmm nn nn nn nn bxaxaxa bxaxaxa bxaxaxa bxaxaxa bxaxaxa 緒 緒 緒 緒 緒 ... .................................................. ... ... ... ... 2211 44242141 33232131 22222121 11212111
- 3. Bentuk Matrik SPL Dalam bentuk matrik SPL dituliskan menjadi, AX=B atau, SPL, AX=B diklasifikasikan menjadi : (a). SPL homogen, jika koefisien matrik B=0 (b). SPL non homogen, jika terdapat koefisien matrik B tak nol n 3 2 1 n 3 2 1 321 3333231 2232221 1131211 b ... b b b x ... x x x ... ............... ... ... ... mnmmm n n n aaaa aaaa aaaa aaaa 633 532 2232 4432 421 431 432 321 緒 緒 緒 緒 xxx xxx xxx xxx CONTOH : SPL non homogen Bentuk matrik SPL 6 5 2 4 3013 3201 2320 0432 4 3 2 1 x x x x
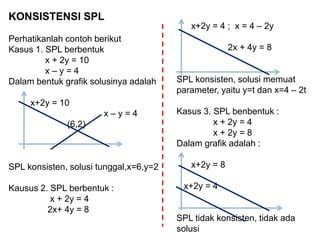
- 4. KONSISTENSI SPL Perhatikanlah contoh berikut Kasus 1. SPL berbentuk x + 2y = 10 x y = 4 Dalam bentuk grafik solusinya adalah x+2y = 10 x y = 4 (6,2) SPL konsisten, solusi tunggal,x=6,y=2 Kausus 2. SPL berbentuk : x + 2y = 4 2x+ 4y = 8 x+2y = 4 ; x = 4 2y 2x + 4y = 8 SPL konsisten, solusi memuat parameter, yaitu y=t dan x=4 2t Kasus 3. SPL benbentuk : x + 2y = 4 x + 2y = 8 Dalam grafik adalah : x+2y = 8 x+2y = 4 SPL tidak konsisten, tidak ada solusi
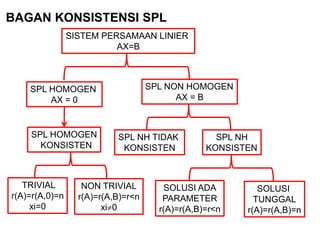
- 5. BAGAN KONSISTENSI SPL SISTEM PERSAMAAN LINIER AX=B SPL HOMOGEN AX = 0 SPL NON HOMOGEN AX = B SPL HOMOGEN KONSISTEN SPL NH TIDAK KONSISTEN SPL NH KONSISTEN TRIVIAL r(A)=r(A,0)=n xi=0 NON TRIVIAL r(A)=r(A,B)=r<n xi0 SOLUSI TUNGGAL r(A)=r(A,B)=n SOLUSI ADA PARAMETER r(A)=r(A,B)=r<n
- 6. Metode Solusi SPL Metode Eliminasi Gouss Metode Eliminasi Gouss Jourdan Metode Crammer Metode Invers Matrik Metode Dekomposisi Matrik Metode Gouss Seidel Metode Jacobi Metode Numerik Solusi dengan program komputer
- 7. METODE ELIMINASI GOUSS OPERASI ELEMENTER BARIS : (1). Hi k Hi : Kalikan sembarang baris ke-I dengan konstanta tak nol k (2). Hi Hj Tukarkanlah semua elemen baris ke-i dengan baris ke-j (3). Hi Hi + kHj Kalikanlah baris ke-j dengan konstanta tak nol k, dan hasilnya jumlahlan pada baris ke-I RANK MATRIK Rank matrik berukuran (mxn) ditulis r(A) adalah banyaknya jumlah baris tak nol dari matrik eselon baris tereduksi. MATRIK ESELON BARIS Matrik eselon baris tereduksi adalah matrik yang mempunyai sifat-sifat sebagai berikut : (1). Jika suatu baris yang elemenya tak nol nol, bilangan pertama pada baris tersebut 1 (1) utama : pivot (2). Jika terdapat baris semua elemen adalah 0, baris spt itu tempatkan pada bagian bawah matrik (3). Jika terdapat 2 baris yang berurutan, 1 utama baris yang lebih rendah terletak jauh kekanan dari pada 1 utama baris yang lebih tingggi. (4). Setiap kolom yang memuat 1 utama, mempunyai 0 did tempat baris yang lebih rendah
- 8. CONTOH : Tentukaan matrik eselon matrik berikut ini Iterasi-1 1 2 3 4 5 8 H1=(1/a11)H1 0 -1 -2 -2 -3 -7 H2=H2-(a21/a11)H1 0 -1 -3 -5 -7 -14 H3=H3-(a31/a11)H1 0 0 1 3 4 7 H4=H4-(a41/a11)H1 0 -1 0 4 5 7 H5=H5-(a51/a11)H1 Matrik Asal 1 2 3 4 5 8 2 3 4 6 7 9 3 5 6 7 8 10 1 2 4 7 9 15 2 3 6 12 15 23 Iterasi-2 1 2 3 4 5 8 0 1 2 2 3 7 H2=(1/a22)H2 0 0 -1 -3 -4 -7 H3=H3-(a32/a22)H2 0 0 1 3 4 7 H4=H4-(a42/a22)H2 0 0 2 6 8 14 H5=H5-(a52/a22)H2 Iterasi-3 1 2 3 4 5 8 0 1 2 2 3 7 0 0 1 3 4 7 H3=(1/a33)H3 0 0 0 0 0 0 H4=H4-(a43/a33)H3 0 0 0 0 0 0 H5=H5-(a53/a33)H3 Dari matrik eselon diperoleh hasil : (1). Jumlah baris tak nol matrik eselon = 3 (2). Rank matrik A, r(A)=3
- 9. METODE ELIMINASI GOUSS Andaikan diberikan SPL dengan m persamaan linier dan n variabel yang tidak diketahui, x1, x2,,xn yaitu : AX = B Langkah-langkah menentukan konsitensi dan solusi SPL non homogen adalah sbb : (1). Bentuk matrik lengkap [A,B] (2). Reduksilah matrik lengkap [AB] menjadi matrik eselon baris tereduksi, E[AB] dengan menggunakan serangkaian operasi elementer baris (3). Dari E[AB], hitunglah rank matrik, r(A) dan r(AB), dengan cara menghitung jumlah baris tak nolnya. (4). Konsistensi SPL (a). Jika r(A)=r(AB)=n, maka SPL konsisten solusi tunggal (b). Jika r(A)=r(AB)=r < n, maka SPL konsisten solusi memuat parameter (c). Jika r(A)r(AB), maka SPL tidak konsisten/tidak ada solusi (5). Solusi SPL (a). Jika SPL konsisten, susunan SPL dari matrik eselon (b). Tentukan solusi SPL dengan cara eliminasi berulang dari xn ke x1
- 10. CONTOH : TIDAK KONSISTEN Tentukanlah solusi SPL jika ada Jawab Matrik lengkap SPL : Operasi elementer baris Reduksi x1 1053 832 522 221 321 321 緒 緒 緒 xxx xxx xxx 10531 8132 5221 ],[ BA ` 5310 2310 5221 H2 H2 2H1 H3 H3 1 H1 Reduksi x2 Jadi, Analisis (1). Jumlah baris tak nol A = 2, sehingga r(A) = 2 (2). Jumlah baris tak nol [A,B]=3, sehingga, r(A,B)=3 (3). Karena r(A)r(A,B), maka SPL tidak konsisten, atau SPL tidak ada solusi ` 3000 2310 5221 H3 H3+H2 ` 3000 2310 5221 ],[ BAE
- 11. CONTOH : SOLUSI PARAMETER Tentukanlah solusi SPL jika ada Jawab Matrik lengkap SPL : 142486 7243 24274 26242 4321 4321 4321 4321 緒 緒 緒 緒 xxxx xxxx xxxx xxxx 142486 71243 24274 26242 ],[ BA Reduksi x1 1 2 -1 3 -1 H1=(1/a11)H1 0 -1 2 -8 6 H2=H2-(a21/a11)H1 0 -2 5 -10 10 H3=H3-(a31/a11)H1 0 -4 10 -20 20 H4=H4-(a41/a11)H1 Reduksi x2 1 2 -1 3 -1 0 1 -2 8 -6 H2=(1/a22)H2 0 0 1 6 -2 H3=H3-(a32/a22)H2 0 0 2 12 -4 H4=H4-(a42/a22)H2 Reduksi x3 1 2 -1 3 -1 0 1 -2 8 -6 0 0 1 6 -2 H3=(1/a33)H3 0 0 0 0 0 H4=H4-(a43/a33)H3
- 12. SOLUSI : SPL Parameter 00000 2-6100 6-82-10 1-31-21 ),( BAE Dari matrik eselon dperoleh hasil : (1). Jumlah baris tak nol A=3, sehingga r(A)=3 (2). Jumlah baris tak nol [A,B]=3, sehingga r(A,B)=3 (3). Jumlah variabel yang tidak diketahui x1,x2,x3,x4 = 4 (4). Jadi r(A)=r(A,B)=3<n=4, maka SPL konsisten dan solusi memuat (n-r=1) parameter 26 682 132 43 432 4321 緒 緒 緒 xx xxx xxxx Solusi : x4 = t, t parameter x3 = 2 6x4 = 2 6t x2 = 6 + 2x3 8x4 = 6 + 2( 2 6t) 8t = 10 20t x1 = 1 2x2 + x3 3x4 =1 2( 10 20t) + ( 2 6t) 3t = 19 + 31t SPL dari matrik eselon
- 13. CONTOH : SOLUSI PARAMETER Tentukanlah solusi SPL jika ada Jawab Matrik lengkap SPL : 1 2 3 4 2 x1 0 2 5 4 6 5 x2 0 3 5 6 7 6 x3 0 1 2 4 7 9 x4 0 2 3 8 10 3 x5 0 0310832 017421 087673 056452 024321 ],[ BA Reduksi x1 1 2 3 4 2 0 H1=(1/a11)H1 0 1 -2 -2 1 0 H2=H2-(a21/a11)H1 0 1 -3 -5 2 0 H3=H3-(a31/a11)H1 0 0 1 3 -1 0 H4=H4-(a41/a11)H1 0 -1 2 2 -1 0 H5=H5-(a51/a11)H1 Reduksi x2 1 2 3 4 2 0 0 1 -2 -2 1 0 H2=(1/a22)H2 0 0 -1 -3 1 0 H3=H3-(a32/a22)H2 0 0 1 3 -1 0 H4=H4-(a42/a22)H2 0 0 0 0 0 0 H5=H5-(a52/a22)H2 Reduksi x3 1 2 3 4 2 0 0 1 -2 -2 1 0 0 0 1 3 -1 0 H3=(1/a33)H3 0 0 0 0 0 0 H4=H4-(a43/a33)H3 0 0 0 0 0 0 H5=H5-(a53/a33)H3
- 14. Dari matrik eselon dperoleh hasil : (1). Jumlah baris tak nol A=3, sehingga r(A)=3 (2). Jumlah baris tak nol [A,B]=3, sehingga r(A,B)=3 (3). Jumlah variabel yang tidak diketahui x1,x2,x3,x4,x5 = 5 (4). Jadi r(A)=r(A,B)=3<n=5, maka SPL konsisten dan solusi memuat (n-r=2) parameter 000000 000000 01-3100 012-2-10 024321 ),( BAE SOLUSI : SPL Parameter Solusi : x5 = s, s parameter x4 = t, t parameter x3 = 3x4 + x5 = 3t + s x2 = 2x3 + 2x4 x5 = 2(3t + s) + 2t s = 4t + s x1 = 2x2 3x3 4x4 2x5 = 2(4t +s) 3(3t+s) 4t 2s = 13t 7s 03 022 02432 543 5432 54321 緒 緒 緒 xxx xxxx xxxxx SPL dari matrik eselon
- 15. CONTOH : SOLUSI TUNGGAL Carilah solusi SPL jika ada Jawab Matrik lengkap SPL adalah : 1342 72243 28274 46242 4321 4321 4321 4321 緒 緒 緒 緒 xxxx xxxx xxxx xxxx 134211 72243 24274 46242 ],[ BA Reduksi x1 1 2 -1 4 2 H1=(1/a11)H1 0 -1 2 -8 -6 H2=H2-(a21/a11)H1 0 -2 5 -10 1 H3=H3-(a31/a11)H1 0 -1 3 0 11 H4=H4-(a41/a11)H1 Reduksi x2 1 2 -1 4 2 0 1 -2 8 6 H2=(1/a22)H2 0 0 1 6 13 H3=H3-(a32/a22)H2 0 0 1 8 17 H4=H4-(a42/a22)H2 Reduksi x3 1 2 -1 4 2 0 1 -2 8 6 0 0 1 6 13 H3=(1/a33)H3 0 0 0 2 4 H4=H4-(a43/a33)H3
- 16. Reduksi x4 1 2 -1 4 2 0 1 -2 8 6 0 0 1 6 13 0 0 0 1 2 H4=(1/a44)H4 Dari matrik eselon dperoleh hasil : (1). Jumlah baris tak nol A=4, sehingga r(A)=4 (2). Jumlah baris tak nol [A,B]=4, sehingga r(A,B)=4 (3). Jumlah variabel yang tidak diketahui x1,x2,x3,x4 = 4 (4). Jadi r(A)=r(A,B)=r=4, maka SPL konsisten dan solusi tunggal SPL dari matrik eselon 2 136 682 242 4 43 432 4321 緒 緒 緒 x xx xxx xxxx Solusi : x4 = 2 x3 = 13 6(2) = 1 x2 = 6 + 2x3 8x4 = 6 + 2(1) 8(2) = 8 x1 = 2 2x2 + x3 4x4 = 2 2(8) + 1 4(2) = 11
- 17. TUGAS : SPL Tentukan solusi SPL berikut ini dengan metode eliminasi Gouss: a ba ba ba ba x x x x x baabb abbaa abbaa baabb baabb 2 2 2 32223 2311 112 211 1112 5 4 3 2 1 10 )(5 105 510 )(10 33121 311 121 111 121 5 4 3 2 1 ba ba ba ba x x x x x bbbab bbbaa bbbaa aaabb aaabb
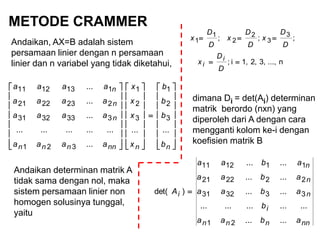
- 18. METODE CRAMMER Andaikan, AX=B adalah sistem persamaan linier dengan n persamaan linier dan n variabel yang tidak diketahui, nnnnnnn n n n b b b b x x x x aaaa aaaa aaaa aaaa ...... ... ............... ... ... ... 3 2 1 3 2 1 321 3333231 2232221 1131211 n...,3,2,1,i; ;;; 3 3 2 2 1 1 緒 緒緒 D D x D D x D D x D D x i i dimana Di = det(Ai) determinan matrik berordo (nxn) yang diperoleh dari A dengan cara mengganti kolom ke-i dengan koefisien matrik B nnnnn i n n n i abaa b abaa abaa abaa A ...... ............... ...... ...... ...... )det( 21 333231 222221 111211 Andaikan determinan matrik A tidak sama dengan nol, maka sistem persamaan linier non homogen solusinya tunggal, yaitu
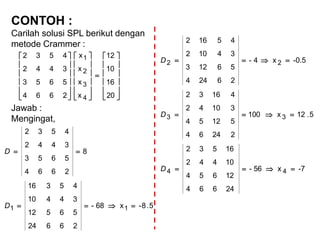
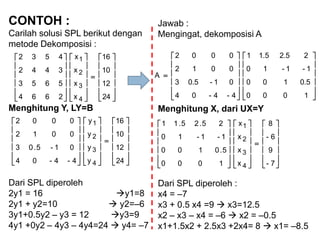
- 19. CONTOH : Carilah solusi SPL berikut dengan metode Crammer : Jawab : Bentuk matrik SPL, AX=B adalah : Karena, 12364 12253 16342 321 321 321 緒 緒 緒 xxx xxx xxx 12 12 16 x x x 364 253 342 3 2 1 4 364 253 342 )det( 緒緒 AD 2 4 8 x 7 4 28 x 9 4 36 x Jadi, 8 1264 1253 1642 )det( 28 3124 2123 3162 )det( 36 3612 2512 3416 )det( 3 3 2 2 1 1 33 22 11 緒 緒 緒 緒緒 緒緒 緒緒 D D D D D D AD AD AD
- 20. CONTOH : Carilah solusi SPL berikut dengan metode Crammer : Jawab : Mengingat, 20 16 10 12 x x x x 2664 5653 3442 4532 4 3 2 1 5.8-x68- 26624 56512 34410 45316 8 2664 5653 3442 4532 11 緒緒 緒 D D -7x56- 24664 12654 10442 16532 5.12x100 22464 51254 31042 41632 -0.5x4- 26244 56123 34102 45162 44 33 22 緒緒 緒緒 緒緒 D D D
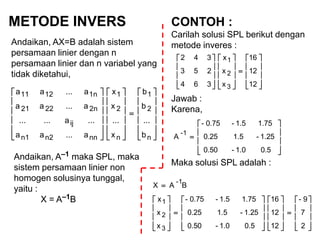
- 21. METODE INVERS Andaikan, AX=B adalah sistem persamaan linier dengan n persamaan linier dan n variabel yang tidak diketahui, n 2 1 n 2 1 nnn2n1 ij 2n2221 1n1211 b ... b b x ... x x a...aa ...a...... a...aa a...aa Andaikan, A1 maka SPL, maka sistem persamaan linier non homogen solusinya tunggal, yaitu : X = A1B CONTOH : Carilah solusi SPL berikut dengan metode inveres : Jawab : Karena, Maka solusi SPL adalah : 12 12 16 x x x 364 253 342 3 2 1 0.51.0-0.50 1.25-1.50.25 1.751.5-0.75- A 1- 2 7 9- 12 12 16 0.51.0-0.50 1.25-1.50.25 1.751.5-0.75- x x x BAX 3 2 1 1-
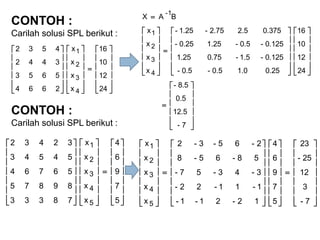
- 22. CONTOH : Carilah solusi SPL berikut : CONTOH : Carilah solusi SPL berikut : 24 12 10 16 x x x x 2664 5653 3442 4532 4 3 2 1 7- 12.5 0.5 8.5- 24 12 10 16 0.251.00.5-0.5- 0.125-1.5-0.751.25 0.125-0.5-1.250.25- 0.3752.52.75-1.25- x x x x BAX 4 3 2 1 1- 5 7 9 6 4 x x x x x 78333 89875 56764 54543 32432 5 4 3 2 1 7- 3 12 25- 23 5 7 9 6 4 12-21-1- 1-11-22- 3-43-57- 58-65-8 2-65-3-2 x x x x x 5 4 3 2 1
- 23. SPL : METODE DEKOMPOSISI Andaikan, AX=B adalah sistem persamaan linier dengan n persamaan linier dan n variabel yang tidak diketahui, n 2 1 n 2 1 nnn2n1 ij 2n2221 1n1211 b ... b b x ... x x a...aa ...a...... a...aa a...aa Andaikan, A dapat didekomposisi menjadi matrik segitiga atas L dan segituga bawah U,akibatnya SPL AX=B dapat ditulis menjadi : LUX = B atau, L Y= B UX = Y Langkah-langkah menentukan solusi SPL non homogen, dengan metode dekomposisi matrik adalah : (1). Tentukan dekomposisi matrik A, menjadi A=LU, dengan metode Crout, Doolite, Cholesky). (2). Tentukanlah nilai Y dari persamaan : LY=B, dengan eliminasi maju (y1, y2, y3, ,yn) (3). Tentukanlah nilai X yang merupakan solusi SPL non homogen, dari persamaan UX=Y dengan eliminasi mundur (xn, xn-1, ,x2,x1).
- 24. CONTOH : Carilah solusi SPL berikut dengan metode Dekomposisi : Jawab : Mengingat, dekomposisi A dengan metode Crout adalah : 12 12 16 x x x 364 253 342 3 2 1 100 5.210 5.121 22-4 01-3 002 LUA Menghitung Y dari LY = B Dari SPL diperoleh : 2y1 = 16 y1=8 3y1 y2 = 12 y2=12 4y1 2y2 + 2y2 = 12 y3 = 2 12 12 16 y y y 22-4 01-3 002 3 2 1 Menghitung X dari UX = Y Dari SPL diperoleh : x3 = 2 x3=2 x2 + 2.5x3 = 12 x2=7 x1 + 2x2 + 1.53 = 2 x1=9 2 12 8 x x x 100 5.210 5.121 3 2 1
- 25. CONTOH : Carilah solusi SPL berikut dengan metode Dekomposisi : Menghitung Y, LY=B Dari SPL diperoleh 2y1 = 16 y1=8 2y1 + y2=10 y2=6 3y1+0.5y2 y3 = 12 y3=9 4y1 +0y2 4y3 4y4=24 y4= 7 24 12 10 16 x x x x 2664 5653 3442 4532 4 3 2 1 1000 0.5100 1-1-10 22.51.51 4-4-04 01-0.53 0012 0002 A Jawab : Mengingat, dekomposisi A Menghitung X, dari UX=Y Dari SPL diperoleh : x4 = 7 x3 + 0.5 x4 =9 x3=12.5 x2 x3 x4 = 6 x2 = 0.5 x1+1.5x2 + 2.5x3 +2x4= 8 x1= 8.5 24 12 10 16 y y y y 4-4-04 01-5.03 0012 0002 4 3 2 1 7- 9 6- 8 x x x x 1000 5.0100 1-1-10 25.25.11 4 3 2 1
- 26. SISTEM TRIDIAGONAL, ALGORITMA THOMAS SPL, dengan bentuk sistem tridiagonal berbentuk, n 1n 3 2 1 n 1n 3 2 1 nn 1n1n 33 222 11 c c ... c c c x x ... x x x fe...000 gf...000 .................. 00...fe0 00...gfe 00...0gf SPL diatas didekomposisi menjadi, A=LU yang berbentuk, n 1n 3 2 1 n 1n 3 2 1 n 1n1n 3 22 11 n 3 2 c c ... c c c x x ... x x x f0...000 gf...000 .................. 00...f00 00...gf0 00...0gf 1e...000 01...000 .................. 00...1e0 00...01e 00...001
- 27. n 1n 3 2 1 n 1n 3 2 1 n 1n1n 3 22 11 y y ... y y y x x ... x x x f0...000 gf...000 .................. 00...f00 00...gf0 00...0gf LANGKAH-LANGKAH SOLUSI (1). Hitung Y dari LY=C, yaitu : (2). Hitung X dari UX=Y, dari : n 1n 3 2 1 n 1n 3 2 1 n 3 2 c c ... c c c y y ... y y y 1e...000 01...000 .................. 00...1e0 00...01e 00...001 ALGORITMA THOMAS : (1). Dekompoisisi DO k=2, n ek=ek/fk1 fk= fk ek.gk1 END DO (2). Forward Substitusi DO k=2,n ck=ck ek.ck1 END DO (3). Back Substitusi xn=cn/fn DO k=n1,1, 1 xk=(ck uk,xk+1)/fk END DO
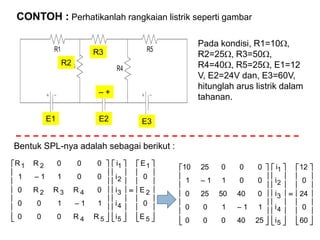
- 28. CONTOH : Perhatikanlah rangkaian listrik seperti gambar Pada kondisi, R1=10, R2=25, R3=50, R4=40, R5=25, E1=12 V, E2=24V dan, E3=60V, hitunglah arus listrik dalam tahanan. 5 2 1 5 4 3 2 1 54 432 21 E 0 E 0 E i i i i i RR000 11100 0RRR0 00111 000RR 60 0 24 0 12 i i i i i 2540000 11100 04050250 00111 0002510 5 4 3 2 1 Bentuk SPL-nya adalah sebagai berikut : R1 R2 R3 V1 V3V2 R5 R4 R2 R3 E1 E2 E3 +
- 30. 10 )(5 105 510 )(10 13112 31123 11234 4321 32112 5 4 3 2 1 ba ba ba ba x x x x x aaabb aaabb aaabb bbbaa bbbaa SOAL-SOAL LATIHAN Carilah solusi SPL berikut ini, dengan metode invers, metode crammer dan dekompoisisi Soal 1 Soal 2 24)5()1()2( )1(16)2()1(2)(a)4( 32)2()1()2( )2(8)1()1()2( 4321 4321 4321 4321 緒 緒 緒 緒 xbxbaxxa bxbxbxxa xbxbxaax axbxbaxxa
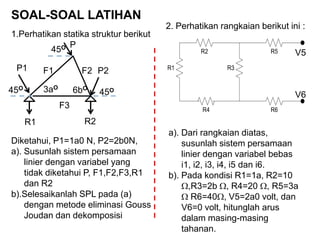
- 31. SOAL-SOAL LATIHAN 1.Perhatikan statika struktur berikut Diketahui, P1=1a0 N, P2=2b0N, a). Susunlah sistem persamaan linier dengan variabel yang tidak diketahui P, F1,F2,F3,R1 dan R2 b).Selesaikanlah SPL pada (a) dengan metode eliminasi Gouss Joudan dan dekomposisi 3aO 6bO 45O 45O 45O P P1 P2F1 F2 F3 R1 R2 R6 R5R2 R4 R3R1 2. Perhatikan rangkaian berikut ini : V5 V6 a). Dari rangkaian diatas, susunlah sistem persamaan linier dengan variabel bebas i1, i2, i3, i4, i5 dan i6. b). Pada kondisi R1=1a, R2=10 ,R3=2b , R4=20 , R5=3a R6=40, V5=2a0 volt, dan V6=0 volt, hitunglah arus dalam masing-masing tahanan.
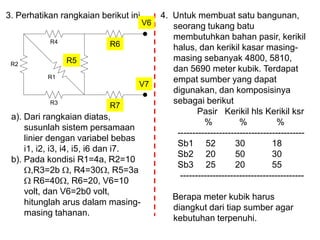
- 32. R1 R2 R3 R3 R6 R4 R5 3. Perhatikan rangkaian berikut ini R5 R6 R7 V6 V7 a). Dari rangkaian diatas, susunlah sistem persamaan linier dengan variabel bebas i1, i2, i3, i4, i5, i6 dan i7. b). Pada kondisi R1=4a, R2=10 ,R3=2b , R4=30, R5=3a R6=40, R6=20, V6=10 volt, dan V6=2b0 volt, hitunglah arus dalam masing- masing tahanan. 4. Untuk membuat satu bangunan, seorang tukang batu membutuhkan bahan pasir, kerikil halus, dan kerikil kasar masing- masing sebanyak 4800, 5810, dan 5690 meter kubik. Terdapat empat sumber yang dapat digunakan, dan komposisinya sebagai berikut Pasir Kerikil hls Kerikil ksr % % % ------------------------------------------- Sb1 52 30 18 Sb2 20 50 30 Sb3 25 20 55 ------------------------------------------ Berapa meter kubik harus diangkut dari tiap sumber agar kebutuhan terpenuhi.