Modul6
- 1. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (1/1) Modul 6 METODE REGULA-FALSI (False Position) untuk Solusi Akar PERSAMAAN ALJABAR NON-LINIER TUNGGAL A. Pendahuluan Seperti telah dijelaskan pada modul terdahulu, Metode Bisection memiliki kelemahan pokok, yaitu: kecepatannya dalam mencapai divergensi; maka beberapa ahli matematika telah berusaha menyempunakan metode tersebut. Namun demikian, metode ini memiliki kelebihan yaitu: kepastian atau jaminannya dalam menuju konvergensi. Dalam modul ini akan dibahas suatu metode solusi baru yang memodifikasi metode bisection, yang kinerjanya lebih cepat dalam mencapai konvergensi, namun masih tetap memiliki kepastian atau jaminan menuju konvergensi. B. Solusi Akar PANLT dengan Metode Regula-Falsi Solusi akar (atau akar-akar) dengan menggunakan Metode Regula- Falsi merupakan modifikasi dari Metode Bisection dengan cara memperhitungkan ‘kesebangunan’ yang dilihat pada kurva berikut: y xαα a b y = f(x) c (b,f(b)) (a,f(a)) P Q R Gambar 6.1. Representasi grafis metode Regula-Falsi.
- 2. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (2/2) Perhatikan kebangunan 2 segitiga Pcb dan PQR di atas, sehingga persamaan berikut dapat digunakan: RQ PR bc Pb = atau ab afbf cb bf − − = − − )()(0)( sehingga       − − −= )()( )(: afbf ab bfbc Persamaan di atas disebut sebagai persamaan rekursif dari Metode Regula Falsi. Kecepatan atau laju konvergensi dari Metode Regula-Falsi sama dengan Metode Bisection, yaitu ‘konvergensi linier’, namun dengan faktor pengali (konstanta) yang lebih besar dari 21 (faktor pengali berkisar antara 21 … 1). C. Algoritma Metode Regula-Falsi Asumsi awal yang harus diambil adalah sama seperti pada Metode Bisection, yaitu: ‘menebak’ interval awal [a,b] dimana f(x) adalah kontinu padanya, demikian pula interval tersebut harus terletak ‘mengapit’ (secara intuitif) nilai akar α, sedemikian rupa sehingga: 0)()( ≤⋅ bfaf Meskipun pada algoritma berikut masih mengandung beberapa kelemahan, namun secara umum masih sangat menguntungkan untuk dipakai. Perbaikan dan modifikasi secara numeris dilakukan oleh Brent (Atkinson, 1978), untuk algoritma tersebut.
- 3. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (3/3) Algoritma REGFAL(f,a,b,akar,ε,iter,itmax,flag) 1. Tebak harga interval [a,b]; tentukan ε; dan itmax 2. Set xold = 2*b-a; iter = 0; flag = 0; 3. Tentukan atau hitung akar = c = b – f(b) [(b – a)/(f(b) – f(a)); iter = iter + 1; 4. Jika f(b)·f(c) ≤ 0 maka a = c jika tidak b = c; 5. Jika abs(c – xold) ≤ ε maka flag = 1 atau jika iter > itmax maka flag = 2 atau jika tidak maka iter = iter + 1 dan akar = c; 6. Jika flag = 0 ulangi ke nomor 3; 7. Selesai. Gambar 6.2. Algoritma Metode-Regula Falsi Sehingga formula rekursif dari Metode REGULA-FALSI: dapat dituliskan dalam resume berikut:    == == <⋅ − − = ++ ++ − + nnnn nnnn nn nn nnnn n bbxa xbaa xfaf afbf afbbfa x 11 11 , , ?0)()( )()( )()( )( )( Adapun sifat atau karakteristik metode ini secara umum adalah: ð Memerlukan 2 harga awal (≡ a0 dan b0 sedemikian rupa sehingga f(a0)·f(b0) ≤ 0) ð Konvergensi Superlinier (≡ Sedang, antara linier dan kuadrat)
- 4. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (4/4) ð Baik digunakan untuk fungsi yang turunannya tak terdefinisi dengan jelas (≡ diskontinyu) ð Divergen (RTE, run time error) bila an = bn (≡ ∆ ≅ εmesin) ð Kriteria penghentian iterasi : ε≤− nn ab dan atau ε≤)( nxf Adapun tabel kerja dari metode ini (sesuai dengan algoritmanya), dapat disajikan secara sistematis sebagai berikut: Tabel 6.1. Tabel Kerja Metode Regula-Falsi n xn an bn f(an) f(bn) 0 --- … … … … 1 … … … … … … … … … … … D. Listing Program Metode Regula-Falsi Diberikan persoalan untuk menghitung akar (akar-akar) persamaan f(x) = 0, sebagai berikut: 0)( 1 =−≡ x exxf Listing program sederhana (non-subroutine) dan program dengan subroutine untuk Metode Regula-Falsi disertakan dalam gambar- gambar 6.2. dan 6.3. di bawah ini, yang ditulis dalam Bahasa FORTRAN 77 (kompatibel dengan Bahasa FORTRAN 90/95):
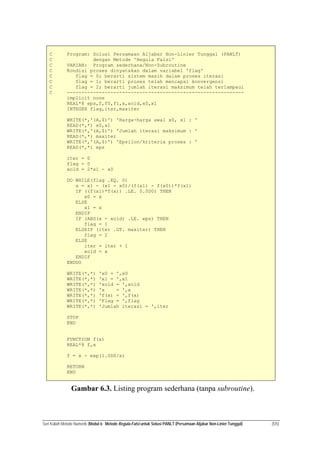
- 5. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (5/5) C Program: Solusi Persamaan Aljabar Non-Linier Tunggal (PANLT) C dengan Metode 'Regula Falsi' C VARIAN: Program sederhana/Non-Subroutine C Kondisi proses dinyatakan dalam variabel 'flag' C flag = 0; berarti sistem masih dalam proses iterasi C flag = 1; berarti proses telah mencapai konvergensi C flag = 2; berarti jumlah iterasi maksimum telah terlampaui C ------------------------------------------------------------- implicit none REAL*8 eps,f,f0,f1,x,xold,x0,x1 INTEGER flag,iter,maxiter WRITE(*,'(A,$)') 'Harga-harga awal x0, x1 : ' READ(*,*) x0,x1 WRITE(*,'(A,$)') 'Jumlah iterasi maksimum : ' READ(*,*) maxiter WRITE(*,'(A,$)') 'Epsilon/kriteria proses : ' READ(*,*) eps iter = 0 flag = 0 xold = 2*x1 - x0 DO WHILE(flag .EQ. 0) x = x1 - (x1 - x0)/(f(x1) - f(x0))*f(x1) IF ((f(x1)*f(x)) .LE. 0.0D0) THEN x0 = x ELSE x1 = x ENDIF IF (ABS(x - xold) .LE. eps) THEN flag = 1 ELSEIF (iter .GT. maxiter) THEN flag = 2 ELSE iter = iter + 1 xold = x ENDIF ENDDO WRITE(*,*) 'x0 = ',x0 WRITE(*,*) 'x1 = ',x1 WRITE(*,*) 'xold = ',xold WRITE(*,*) 'x = ',x WRITE(*,*) 'f(x) = ',f(x) WRITE(*,*) 'Flag = ',flag WRITE(*,*) 'Jumlah iterasi = ',iter STOP END FUNCTION f(x) REAL*8 f,x f = x - exp(1.0D0/x) RETURN END Gambar 6.3. Listing program sederhana (tanpa subroutine).
- 6. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (6/6) C Program: Solusi Persamaan Aljabar Non-Linier Tunggal (PANLT) C dengan Metode 'REGULA-FALSI' C VARIAN: Program dengan Subroutine C ------------------------------------------------------------- implicit none external f REAL*8 eps,f,x,x0,x1 INTEGER flag,iter,maxiter WRITE(*,'(A,$)') 'Harga-harga awal x0, x1 : ' READ(*,*) x0,x1 WRITE(*,'(A,$)') 'Jumlah iterasi maksimum : ' READ(*,*) maxiter WRITE(*,'(A,$)') 'Epsilon/kriteria proses : ' READ(*,*) eps CALL REGFAL(f,x0,x1,x,eps,iter,maxiter,flag) WRITE(*,*) 'x0 = ',x0 WRITE(*,*) 'x1 = ',x1 WRITE(*,*) 'x = ',x WRITE(*,*) 'xold = ',x WRITE(*,*) 'f(x) = ',f(x) WRITE(*,*) 'Flag = ',flag WRITE(*,*) 'Jumlah iterasi = ',iter STOP END FUNCTION f(x) REAL*8 f,x f = x - exp(1.0D0/x) RETURN END SUBROUTINE REGFAL(ff,x0,x1,x,eps,itnum,itmax,prflag) C -------------------------------------------------------- C Sub-program: Solusi PANLT dengan metode REGULA-FALSI | C sebagai perbaikan dari metode BISECTION | C ff : fungsi f(x) = 0 yang akan dicari akarnya | C x0 : nilai x-awal di sebelah kiri akar f(x) | C x1 : nilai x-awal di sebelah kanan akar f(x) | C x : akar f(x), nilai paruh (antara x0 dan x1) | C eps : kriteria atau ketelitian penghitungan | C itnum : jumlah iterasi yang dilakukan proses | C itmax : jumlah pembatas iterasi untuk proses | C prflag : identifikasi untuk konvergensi, yaitu: | C 0 = proses sedang/akan berlangsung | C 1 = proses mencapai konvergensinya | C 2 = itmax telah terlampaui | C -------------------------------------------------------- REAL*8 eps,ff,x,xold,x0,x1 INTEGER prflag,itnum,itmax
- 7. Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (7/7) itnum = 0 prflag = 0 xold = 2*x1 - x0 DO WHILE(prflag .EQ. 0) x = x1 - (x1 - x0)/(ff(x1) - ff(x0))*ff(x1) itnum = itnum + 1 IF ((ff(x1)*ff(x)) .LE. 0.0D0) THEN x0 = x ELSE x1 = x ENDIF IF (ABS(x - xold) .LE. eps) THEN prflag = 1 ELSEIF (itnum .GT. itmax) THEN prflag = 2 ELSE xold = x ENDIF ENDDO RETURN END Gambar 6.4. Listing program dengan subroutine. Tugas: Cari akar (akar-akar) dari persamaan: )ln()( xexf x ⋅= − ! E. Pustaka yang bersesuaian Atkinson, Kendal E., “An Introduction to Numerical Analysis”, John Wiley & Sons, Toronto, pp. 44-48, 1978. Atkinson, L.V., Harley, P.J., “An Introduction to Numerical Methods with Pascal”, Addison-Wesley Publishing Co., Tokyo, pp. 49-51, 1983. Bismo, Setijo, “Modul Kuliah Metode Numerik”, TGP-FTUI, 1999.


![Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (2/2)
Perhatikan kebangunan 2 segitiga Pcb dan PQR di atas, sehingga
persamaan berikut dapat digunakan:
RQ
PR
bc
Pb
=
atau
ab
afbf
cb
bf
‚àí
‚àí
=
‚àí
‚àí )()(0)(
sehingga
Ô£∫

Ô£π

Ô£∞

‚àí
‚àí
‚àí=
)()(
)(:
afbf
ab
bfbc
Persamaan di atas disebut sebagai persamaan rekursif dari
Metode Regula Falsi.
Kecepatan atau laju konvergensi dari Metode Regula-Falsi sama
dengan Metode Bisection, yaitu ‘konvergensi linier’, namun
dengan faktor pengali (konstanta) yang lebih besar dari 21 (faktor
pengali berkisar antara 21 … 1).
C. Algoritma Metode Regula-Falsi
Asumsi awal yang harus diambil adalah sama seperti pada Metode
Bisection, yaitu: ‘menebak’ interval awal [a,b] dimana f(x) adalah
kontinu padanya, demikian pula interval tersebut harus terletak
‘mengapit’ (secara intuitif) nilai akar α, sedemikian rupa sehingga:
0)()( ≤⋅ bfaf
Meskipun pada algoritma berikut masih mengandung beberapa
kelemahan, namun secara umum masih sangat menguntungkan
untuk dipakai. Perbaikan dan modifikasi secara numeris dilakukan
oleh Brent (Atkinson, 1978), untuk algoritma tersebut.](https://image.slidesharecdn.com/modul6-150516233438-lva1-app6892/85/Modul6-2-320.jpg)
![Seri Kuliah Metode Numerik (Modul 6: Metode Regula-Falsi untuk Solusi PANLT (Persamaan Aljabar Non-Linier Tunggal) (3/3)
Algoritma REGFAL(f,a,b,akar,ε,iter,itmax,flag)
1. Tebak harga interval [a,b]; tentukan ε;
dan itmax
2. Set xold = 2*b-a; iter = 0; flag = 0;
3. Tentukan atau hitung akar = c = b –
f(b) [(b – a)/(f(b) – f(a)); iter = iter + 1;
4. Jika f(b)·f(c) ≤ 0 maka a = c jika tidak
b = c;
5. Jika abs(c – xold) ≤ ε maka flag = 1
atau jika iter > itmax maka flag = 2
atau jika tidak maka iter = iter + 1 dan
akar = c;
6. Jika flag = 0 ulangi ke nomor 3;
7. Selesai.
Gambar 6.2. Algoritma Metode-Regula Falsi
Sehingga formula rekursif dari Metode REGULA-FALSI: dapat
dituliskan dalam resume berikut:
Ô£≥
Ô£≤
Ô£±
==
==
<‚ãÖ
‚àí
‚àí
=
++
++
‚àí
+
nnnn
nnnn
nn
nn
nnnn
n
bbxa
xbaa
xfaf
afbf
afbbfa
x
11
11
,
,
?0)()(
)()(
)()(
)(
)(
Adapun sifat atau karakteristik metode ini secara umum adalah:
ð Memerlukan 2 harga awal (≡ a0 dan b0 sedemikian rupa
sehingga f(a0)·f(b0) ≤ 0)
ð Konvergensi Superlinier (≡ Sedang, antara linier dan kuadrat)](https://image.slidesharecdn.com/modul6-150516233438-lva1-app6892/85/Modul6-3-320.jpg)