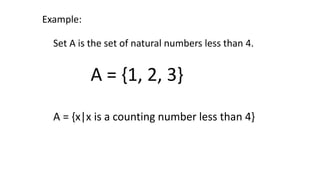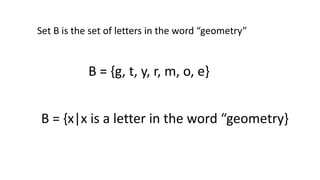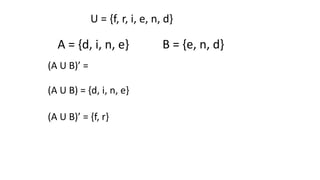Module week 1 Q1
- 3. What is a set? A group or collection of objects Each objects in a set is called a MEMBER or an ELEMENT of a set ð ð
- 4. (ellipsis)
- 5. Which of the following sets are well â defined? The sets of all large numbers. The set of all multiples of 5. The set of good citizens. The set of honest students in your class
- 6. Representation of set 1) A set is denoted by a capital letter. Example : set A, set B, set N etc. 2) The elements of a set are denoted by small letters. All elements are written in { } (curly) brackets separated by , (comma). Example : {a,b,c,x ,y} 3) In set notation, elements are not repeated. Example : A is a set of letters in the word good , then set A = { g,o,d}. 4) The order of elements in a set does not matter.
- 7. Three ways of writing a Set Roster Notation or Listing Method In roster form, all the elements of a set are listed, the elements are being separated by commas and are enclosed within braces { }
- 9. A is a set of whole numbers less than 6. A = { 0,1,2,3,4,5} C is the set of letters in the word excellent C = { e, x, c, l, n, t }
- 10. Set-builder form ( Rule method) In this method , we specify the rule or property or statement. This method lists the rules that determine whether an object is an element of the set or not. A = { x | x has a property of p} This is read as A is the set of elements x such that( | ) x has a property p.
- 11. Verbal Description Method a verbal description of a set uses an English sentence to state a rule that allows us to determine the class of objects being discussed and to determine for any particular object whether or not it is in the set Set A is the set of natural numbers less than 4. Set B is the set of letters in the word âgeometryâ
- 12. We have three ways of describing sets: by name or verbal description of the elements of a set, by roster (list) form by listing the elements separated by commas and using braces to enclose the list, by set-builder notation that uses a variable and a rule to describe the elements of a se
- 13. Set A is the set of natural numbers less than 4. Example: A = {1, 2, 3} A = {x|x is a counting number less than 4}
- 14. Set B is the set of letters in the word âgeometryâ B = {g, t, y, r, m, o, e} B = {x|x is a letter in the word âgeometry}
- 15. A set either be FINITE or INFINITE. FINITE = if the elements in it can be counted INFINITE = if the elements in it cannot be counted The number of elements is a set A is called the CARDINAL NUMBER of A or the cardinality of A. In symbols, we write n(A) or |A|
- 16. Let P = {5, 10, 15, 20, 25, 30} Then, P is a finite set and n(P) = 6 Let Q = {natural numbers less than 25} Then, Q is a finite set and n(P) = 24 Let R = {whole numbers between 5 and 45} Then, R is a finite set and n(R) = 38 The set of all students in Munsci
- 17. Set of all points in a plane is an infinite set Set of all positive integers which is multiple of 3 set of all whole numbers is an infinite set W = {0, 1, 2, 3, âĶâĶ..} set of all natural numbers is an infinite set N = {1, 2, 3, âĶâĶâĶ.}
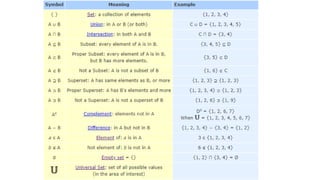
- 18. Common Symbols Used in Set Theory
- 19. â
- 21. Equal and Equivalent Sets Set A and C are EQUAL sets Set A and set B are equivalent sets. These sets are not equal.
- 22. Two sets are equal if and only if they contain exactly the same element. Two sets are equivalent if and only of there is a one-to-one correspondence between the sets. Remember! One-to-one correspondence pairs the element of two sets so that, for each element of one set, there is exactly one element of the other. The two sets have the same cardinality.
- 23. 1.Equal Sets 2.Equal sets 3.Not equal but Equivalent Sets
- 24. Think about this!!! If two sets are equivalent, are they equal? If two sets are equal, are they equivalent?
- 25. UNIVERSAL SETS, SUBSETS, and , VENN DIAGRAM A = {1, 2, 3,4} B = {2, 4} C = {2, 3, 5, 7} D = {1, 2, 3, 4}
- 26. The set of number in the 10 cards is U = {1, 2, 3, 4, 5, 6, 7, 8, 9 , 10} The universal set, or simply the universe, denoted by U, contains all elements being considered in a given situation. The other sets are defined as follows: A = {1, 2, 3,4} B = {2, 4} C = {2, 3, 5, 7} D = {1, 2, 3, 4}
- 27. A = {1, 2, 3,4} B = {2, 4} C = {2, 3, 5, 7} D = {1, 2, 3, 4} Notice that every member of B is also a member of A. B â ðī ðð ðĩ â ðī ðĩ â ðī means that A has at least one element that is not in B. The symbol â suggest proper inclusion. We write D â A but not D â ðī since A has no member that is not in D. Thus, D â A
- 28. Generalization! B = {1, 2, 3, 4}A = {2, 4}
- 29. 1. Subset 2. Not subset. Triangle is just an element of the set. 3. Subset 4. Not subset, since it has an element of heart. 5. Subset. Empty set has no element. Hence, it is true that there is no element in {} that is not element of NOTE: Empty set is subset of every set because every element in the empty set belongs to any set since the empty set has no elements.
- 30. Determine how many subsets of the following: A = {1, 2, 3} A contains 3 elements. So, n = 3 Then, the number of subsets is = 23 = 8 the formula to find the number of subsets for A is given by 2n And also, the formula to find the number of proper subsets is given by 2n-1 {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}, { } Proper subsets of A : {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, { } Note : A subset which is not a proper subset is called as improper subset. The improper subset of a given set is the set itself. Improper subset of A : {1, 2, 3}
- 32. A Venn diagram, also called primary diagram, set diagram or logic diagram, is a diagram that shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. Venn diagram John Venn
- 34. INTERSECTION the intersection of two sets A and B, denoted by A âĐ B, is the set containing all elements of A that also belong to B (or equivalently, all elements of B that also belong to A).
- 35. INTERSECTION Given: A = {p, u, r, e} and B = {h, e, a, r, t} the intersection of two sets A and B, denoted by A âĐ B, is the set containing all elements of A that also belong to B (or equivalently, all elements of B that also belong to A). A âĐ B = {r, e} Given: A = {2, 4, 6, 8} and B = {1, 3, 5, 7} A âĐ B = {} or â
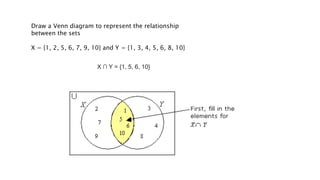
- 36. Draw a Venn diagram to represent the relationship between the sets X = {1, 2, 5, 6, 7, 9, 10} and Y = {1, 3, 4, 5, 6, 8, 10} X âĐ Y = {1, 5, 6, 10}
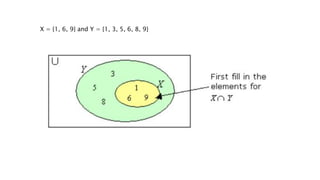
- 37. X = {1, 6, 9} and Y = {1, 3, 5, 6, 8, 9}
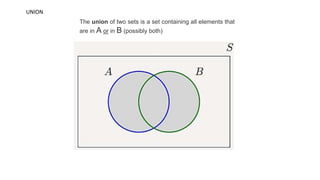
- 38. UNION The union of two sets is a set containing all elements that are in A or in B (possibly both)
- 39. UNION The union of two sets is a set containing all elements that are in A or in B (possibly both) Given: A = {p, u, r, e} and B = {h, e, a, r, t} A U B = {p, u, r, e, h, a, t} Given: A = {l, o, v, e} and B = {h, a, t, e} A U B = {l, o, v, e, h, a, t}
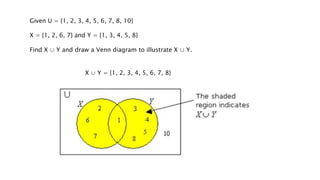
- 40. Given U = {1, 2, 3, 4, 5, 6, 7, 8, 10} X = {1, 2, 6, 7} and Y = {1, 3, 4, 5, 8} Find X ⊠Y and draw a Venn diagram to illustrate X ⊠Y. X ⊠Y = {1, 2, 3, 4, 5, 6, 7, 8}
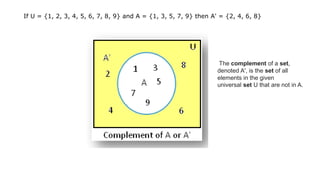
- 41. COMPLEMENT The complement of a set, denoted A', is the set of all elements in the given universal set U that are not in A. U = {f, r, i, e, n, d} A = {d, i, n, e} B = {e, n, d} Aâ = {f, r} Bâ = {f, r, i}
- 42. (A U B)â = U = {f, r, i, e, n, d} A = {d, i, n, e} B = {e, n, d} (A U B) = {d, i, n, e} (A U B)â = {f, r}
- 43. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9} and A = {1, 3, 5, 7, 9} then A' = {2, 4, 6, 8} The complement of a set, denoted A', is the set of all elements in the given universal set U that are not in A.
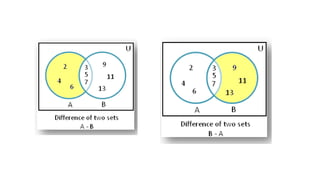
- 44. DIFFERENCE The relative complement or set difference of sets A and B, denoted A â B, is the set of all elements in A that are not in B. A = {d, i, n, e} B = {e, n, d} A - B = {i}
- 45. If A = {2, 3, 4, 5, 6, 7} and B = {3, 5, 7, 9, 11, 13} Find A â B and B â A.
- 47. Venn Diagram