Motor asinkron rotor sangkar
- 1. 1 MOTOR ASINKRON ROTOR SANGKAR 1. PERCOBAAN STATIS Percobaan ini meliputi : ’é¦ Pembacaan plat nama (nama plate) ’é¦ Pengukuran tahanan belitan mesin asinkron ’é¦ Pengujian tahanan isolasi 1.1. Tujuan Umum Dan Khusus a. Membiasakan diri dalam memperhatikan besaran nominnal mesin yang diperbolehkan b. Mencatat harga nominal mesin yang akan diuji coba c. Membiasakan diri melakukan pengecekan mesin sebelum mesin diuji coba atau dijalankan d. Melakukan tindakan pengamanan awal terhadap mesin yang akan diuji coba e. Mengerti dan bisa melakukan pengukuran tahanan mesin asinkron f. Mengukur tahanan-tahanan belitan mesin asinkron yang akan diuji coba g. Mengukur besarnya tahanan isolasi antara terminal-terminal dan antara terminal dengan badan mesin asinkron 1.2. Dasar Teori Sebelum menjalankan mesin (melakukan percobaan), penting skali untuk memeriksa dengan seksama harga-harga nominal dari sebuah mesin. Data ini dicantumkan pada setiap mesin oleh pabrik pembuatannya. Dengn demikian, setiap orang yang akan memakainya mengenal hal-hal penting yang brehubungan dengan data atau nilai kerjanya. Harga nominal ini merupakan hasil pengujian pabrik pembuatannya. Oleh karena itu, untuk
- 2. 2 membuktikan edata yang diberikan pabrik, perlu dilakukan pengujian pada mesin tersebut. Untuk meyakinkan keamanan pada setiap mesin yang akan kita jalankan, perlu sekali melihat apakah mesin itu masaih baik, ditinjau dari segi isolasinya. Standar isolasi pada setiap peralatan listrik telah ditetapkan dengan rekomendasi IEC. Pada keperluan khusus, diperlukan sekali untuk mengetahui tahanan- tahanan belitan mesin asinkron, seperti untuk mencari efesiensi konvensional, torsi dan slip dalam keadaan berbeban, mencari sifat dari kerja mesin itu. Cara mengukurnya, dapat menggunakan multimeter (ohmmeter) atau dengan voltmeter-ampermeter. 1.3. Peralatan Yang Digunakan 1. mesin asinkron rotor sangkar 3 fasa 2. amperemeter dan voltmeter 3. multimeter (ohmmeter) 4. isolating testmeter atau megger 5. kabel 1.4. Langkah Percobaan 1. Mencatat data yang tercantum pada plat nama motor yang akan diuji coba 2. Mengukur tahanan belitan stator (u1-u2, v1-v2 dan w1-w2) dengan ohmmeter 3. Mengukur tahanan belitan stator (u1-u2, v1-v2 dan w1-w2) dengan metode voltmeter-amperemeter seperti pada gambar 1.1 4. Mengukur tahanan isolasi antara belitan stator (u1-u2, v1-v2 dan w1-w2) dan tahanan antarabelitan statorr dengan rangka mesin dengan ohmmeter dan dengan isolating testmeter
- 3. 3 1.5. Rangkaian Percobaan Metode voltmeter amperemeter A RS V W1 W2 V1U1 V2U2 Gambar 1.1 Rangkaian percobaan untuk pengukuran tahanan belitan motor.
- 4. 4 2. PERCOBAAN DINAMIS 2.1 Tujuan Umum a. Mengetahui cara kerja motor asinkron rotor sangkar b. Dapat mengoperasikan motor asinkon rotor sangkar c. Dapat menentukan rangkaian ekivalen motor asinkron d. Dapat menganalisa pengaruh pembebanan terhadap putaran motor asinkron rotor sangkar 2.2 Tujuan Khusus 1. Karakteristik beban nol : Io = f(Vo), Po = f(Vo), cos’ü” = f (Vo) ’é¦ Mengetahui pengaruh tegangan masukan terhadap arus, daya faktor daya motor asinkron ’é¦ Mencari komponen arus magnetisasi kerugian mekanik (kerugian gesekan bantalan dan udara dan kerugian besi) 2. Karakteristik hubungan singkat : Phs = f(Ihs), Vhs = f(Ihs), cos’ü” = f(Ihs) pada s =1 (n=0) ’é¦ Mengetahui pengaruh arus hubungansingkat : terhadap daya, tegangan dan faktor daya motor asinkron ’é¦ Mencari komponen rangkaian pengganti Xek dan Rek pada rangkaian ekivalen motor asinkron dilihat dari sisi stator ’é¦ Mencari nilai arus hubungan singkat pada saat tegangan nominal 3. Mencari rangkaian ekivalen motor asinkron dengan data yang telah diperoleh 4. Mencari karakteristik berbenaan motor asinkron : n = f(P)
- 5. 5 2.3 Dasar Teori Motor induksi merupakan motor arus bolak-balik yang paling luas digunakan. Penamaannya berasal dari kenataan bahwa arus rotor motor ini bukan diperoleh dari sumber tertentu, tetapi merupakan arus yang terinduksi sebagai akibata adanya perbedaab relatif antara putaran rotor dengan medan putaar (rotating magnetik field) yang dihasilkan oleh arus stator. Belitan stator yang dihubungkan dengann sumber tegangan tiga fase akan menghasilkan medan magnet yang berputar dengan keceptan sinkron (ns = 120f/p, dimana f adalah frekuensi dan p adalah jumlah kutub). Medan putar pada stator tersebut akan memotong konduktor- konuktor pada rotor, sehingga terinduksi arus; dan sesuai dengan hukum Lentz, rotorpun akan turut berputar mengikuti medan putar stator. Perbedaaan putaran relatif antara stator dan rotor disebut slip. Bertambahnya beban akan memperbesar kopel motor, yangoeh karenanya akan memperbesar pula arus induksi pada rotor, sehingga slip antara medan putar stator dan putaran rotor pun akan bertambah besar. Jadi bila beban motor bertambah, putaran rotor cenderung menurun. Dikenal 2 tipe motor induksi, yaitu motor induksi dengan rotor sangkaar dan motor induksi dengan rotor belitan. Kerja motor induksi seperti juga kerja transformator adalah berdasarkan prinsip induksi electromagnet. Oleh karena itu, motor induksi dinggap sebaagai transformator dengan rangkaian sekunder yang berputar, sehingga rangkaian ekivalehnnya hampir sama. Rangkaian ekivalen motor induksi dapat digambarkan sebagai berikut :
- 6. 6 I1 R1 X1 a R2 a R2 a R2 (1-S)/S Rc XMn Gambar 2.1. rangkaian ekivalen motor induksi Karakteristik Beban Nol Uji tanpa beban dilakuka dengan cara mensuplai motor sampai dengan tegangan nominal dan membiarkan roto berputar tanpa torsi pengereman. Dalamhal ini arus masukan digambarkan sebagai jumlah vektor arus magenetisasi dan arus aktif yang disebabkan rugibesi (stator) dan rugi mekanik (friksi dan angin). Daya masukan sama dengan jumlah semua rugi keadaan tanpa beban, yaitu rugi tembaga stator, rugi besi dan rugimekanik (friksi dan angin). Dengan mengukur arus beban nol (Io), tegangan beban nol (Vo) dan daya pada kondisi beban nol (Po), maka cos’ü” beban nol dapat dihitung. Bentuk karakteristik pada pengujian motor induksi tanpa yang berupa kurva Io = f(Vo), Po = f(Vo) dan cos’ü” = f(Vo) dapat digambarkan seperti gambar 2. Gambar2.2. karakteristik beban nol I0, P0, Cos├ś I0 P0 Cos ├ś V0
- 7. 7 Dari data pegujian beban nol, maka parameter RC dan XM dapat dihitung dengan persamaan : RC = ; 0 0 2 P V XM = 0 2 0 2 0 2 0 PIV V ’ĆŁ Karakteristik Hubung Sigkat (Rotor Ditahan) Apabila rotor di blok / ditahan, maka arus input hanya dibatasi oleh impedansi ekivalen belitannya (resistansi dan reaktansi bocor). Oleh karena itu, jika dalam kondisi ini motor disuplai dengan tegangan n ominal, maka akan terjadi arus yang sangat tinggi yang secara teknis dapat mrusak belitan, sehingga pada pengujian hubung singkat biasanya dilaksanakan dengan mensuplai motor dengan tegangan yang diturunkan secukupnya sampai arustudak melebihi nilai nominalnya. Besar-besaran pada saat tegangan nominal merupakan harga yang dicari dan dihitung dengan menggunakan perbandingan arus dan tegangannya. Hal ini dianggap bahwa apabila tegangan suplai bervariasi, reaktansi bocor dan resistansi belitan tetap konstan. Dari percobaan hubungan singkat diperoleh data : arus hubung singkat (Ihs), tegangan hubungan singkat (Vhs) dan daya hubung singkat per fase (Phs), maka parameter Rek = R1 + a2 R2 dan Xek = X1 + a2 X2 dapat dihitung dengan persamaan : Rhsn= ;2 hs hs I P Xek= 2 222 hs hshshs I PIV ’ĆŁ Dengan mengingat bahwa uji hubung singkat dilakukan dengan tegangan yang diturunkan, maka harga arus hubung singkat dan daya hubung singkat pada tegangan nominal (Ihsn dan Phsn) dapat dihitung dengan persamaan : Ihsn = Ihs hs n V V ; Phsn = 3Vn Ihsn Cos ’ü” hs
- 8. 8 Hasil pengujian dapat digambarkan karakteristik hubung singkat yang berupa kurva daya ubung singkat (Phs), tegangan hubung singkat (Vhs) dan cos ’ü” hs sebagai fungsi arus yang diserap (Ihs). Gambar 2.3 karakteristik hubung singkat Biasanya grafik tegangan adalah linier, grafik cos ’ü” hs adalah konstan dan grafik daya adalah parabola. Daya ini merupakan kerugian, antara lain : kerugian berupa panas dalam belitan stator rotor serta rugi tambahan dalam tembaga rotor. Rugi tambahan dalam tembaga rotor disebabkan oleh frekuensi fluksi yang tinggi yang memotongnya (sama dengan frekuensi suplai) yang menimbulkan arus eddy dalam rotor itu sendiri. Oleh karena itu, daya berupa panas bertambah besar kalau dibandingkan dengan daya hilang selama operasi normal ketika frekuensi rotor sangat rendah. Karakteristik Putaran vs Beban Seperti motor-motor penggerak lainnya,penting sekali mengetahui adanya karakteristik putaran fungsi dari beban. Sudah menjadi sifat mesin asinkron, bahwa berputar motor itu akibat adanya slip antara medan stator dan rotor, slip ini akan menjadi besar apabila beban bertambah. Vhs, Phs, Cos├ś Vhs Phs Cos├ś Ihs
- 9. 9 2.4 Peralatan Yang Digunakan 1. Mesin asinkron rotor sangkar 3 fase 2. Amperemeter dan voltmeter 3. Multimeter (ohmmeter) 4. Wattmeter dan trafo. Arus 5. Rpm meter 6. Regulator 3 fasa 7. Kabel 2.5 Langkah Percobaan 1. Mencari Karakteristik Beban Nol ’é¦ Membuat rangkaian percobaan untuk mencari karakteristik beban nol. ’é¦ Membuat urutan kerjanya. Tegangan diatur dari nol sampai tegangan nominal. Pengambilan data dilakukan dari tegangan yang paling tinggi (tegangan nominal) dan diturunkan secara bertahap. ’é¦ Mencatat hasil pengukuran kedalam tabel yang tersedia 2. Mencari Karakteristik Hubungan Singkat ’é¦ Membuat rangkaian percobaan unuk mencari karakteristik hubung singkat ’é¦ Membuat urutan kerjanya ’é¦ Mencatat hasil pengukuran kedalam tabel yang tersedia 3. Mencari Karakteristik Pytaran vs Beban ’é¦ Membuat rangkaian percobaan untuk mencari karakteristik hubung singkat. ’é¦ Membuat urutan kerjanya, dalam hal inimotor dibebani dengan generator DC ’é¦ Mencatat hasilpengukuran kedalam tabel yang tersedia
- 10. 10
- 11. 11 RANGKAIAN PERCOBAAN MOTOR ASINKRON ROTOR SANGKAR Gambar 2.4 Rangkaian Percobaan Motor Asinkron Rotor Sangkar V A R I A C G A V SUMBER DC A V R M V V A W A A n L1 L2 L3 N
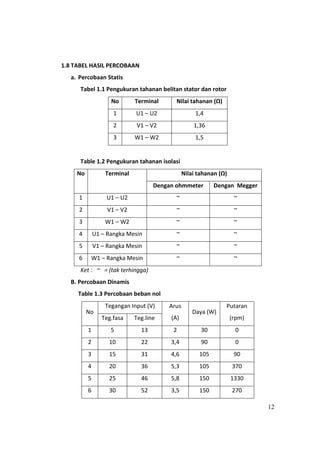
- 12. 12 1.8 TABEL HASIL PERCOBAAN a. Percobaan Statis Tabel 1.1 Pengukuran tahanan belitan stator dan rotor No Terminal Nilai tahanan (Ōä”) 1 U1 ŌĆō U2 1,4 2 V1 ŌĆō V2 1,36 3 W1 ŌĆō W2 1,5 Table 1.2 Pengukuran tahanan isolasi No Terminal Nilai tahanan (Ōä”) Dengan ohmmeter Dengan Megger 1 U1 ŌĆō U2 ~ ~ 2 V1 ŌĆō V2 ~ ~ 3 W1 ŌĆō W2 ~ ~ 4 U1 ŌĆō Rangka Mesin ~ ~ 5 V1 ŌĆō Rangka Mesin ~ ~ 6 W1 ŌĆō Rangka Mesin ~ ~ Ket : ~ = (tak terhingga) B. Percobaan Dinamis Table 1.3 Percobaan beban nol No Tegangan Input (V) Arus (A) Daya (W) Putaran (rpm)Teg.fasa Teg.line 1 5 13 2 30 0 2 10 22 3,4 90 0 3 15 31 4,6 105 90 4 20 36 5,3 105 370 5 25 46 5,8 150 1330 6 30 52 3,5 150 270
- 13. 13 Table 1.4 Percobaan hubung singkat (n=0) No Tegangan Input (V) Arus (A) Daya (W) Teg.fasa Teg.line 1 3 9 1 30 2 6 13 2 30 3 11 19 3 30 4 15 27 4 60 5 18 33 5 60 6 22 41 6 90 Table 1.5 Percobaan berbeban No Motor Asinkron Generator DC Beban (Ōä”) VL (V) Vp (V) I (A) P (W) N (rpm) Iex (A) VL (V) IL (A) 1 57 35 5,6 150 2500 0,2 2,3 ~ 0 2 56 34 8,7 150 880 69 0,18 415 3 56 34 8,7 175 770 60 0,2 348,5 4 56 34 8,8 175 670 54 0,22 280,1 5 56 34 8,8 175 570 45 0,24 213,5 6 56 34 8,9 200 530 39 0,26 191,4 7 56 34 9 200 499 36 0,26 170,1 8 55 34 9 200 440 33 0,27 157,6 9 54 34 9 200 420 30 0,27 139,4 10 55 34 9,1 200 390 27 0,28 130,6
- 14. 14 1.9 ANALISA HASIL PERCOBAAN Tanpa Beban Sebagai contoh perhitungan diambil data Nomor 3: Dik : I = 4,6 A P = 105 W V = 31 V Dit : I = ........................? Cos ├ś = ...........................? Penyelesaian : I = 4,6 A Cos ├ś = IV P L ’é┤’é┤3 = 6,4313 105 ’é┤’é┤ = 0,42 Dengan cara yang sama untuk analisa data selanjutnya Tabel 1.7 Hasil analisa data percobaan tanpa beban No V I Cos├ś P (V) (A) (W) 1 13 2 0,66 30 2 22 3,4 0,69 90 3 31 4,6 0,42 105 4 36 5,3 0,31 105 5 46 5,8 0,32 150 6 52 3,5 0,47 150
- 15. 15 Hubung singkat Sebagai contoh perhitungan diambil data Nomor 3: Dik : Ihs = 3 A Phs = 30 W Vp = 11 Volt VL = 19 Volt Dit : - Ihs = ..........................? - Cos ├ś = ..........................? Penyelesaian : ’āś Ihs = 3 A ’āś Cos ├ś = hsL hs IV P ’é┤’é┤3 = 3193 30 ’é┤’é┤ = 0.30 Dengan cara yang sama untuk analisa data selanjutnya Tabel 1.6 Hasil analisa data percobaan hubung singkat No V (V) Ihs (A) Cos├ś P (W) 1 9 1 1,92 30 2 13 2 0,66 30 3 19 3 0,30 30 4 27 4 0,32 60 5 33 5 0,20 60 6 41 6 0,21 90
- 16. 16 Berbeban Sebagai contoh perhitungan diambil data Nomor 3: Dik : I = 8,7 A P = 175 W f = 50 Hz Nr = 3050 rpm Vm = 270 V Dit : Im =...........................? Cos ├ś =..............................? Nstator =...........................? Slip = ..........................? Torsi = ..........................? Penyelesaian : Im = 5,6 A Cos ├ś = mL IV P ’é┤’é┤3 = 7,8563 175 ’é┤’é┤ = 0.20 Nstator = p f’é┤120 = 2 50120’é┤ = 3000 rpm Slip (S) = s rs n nn ’ĆŁ = 3000 7703000’ĆŁ = 0,73 Torsi (T) = rn P ’é┤’é┤ ’é┤ ’ü░2 60 = 77014,32 17560 ’é┤’é┤ ’é┤ = 2,17 Nm Tabel 2.9 Hasil analisa percobaan berbeban No Vm (V) P (W) n (Rpm) T (Nm) Cos├ś Slip (S) 1 57 150 2500 0,57 0,27 0,16 2 56 150 880 1,62 0,17 0,70 3 56 175 770 2,17 0,20 0,73 4 56 175 670 2,49 0,20 0,77 5 56 175 570 2,93 0,20 0,81 6 56 200 530 3,60 0,23 0,82 7 56 200 490 3,89 0,22 0,83 8 55 200 440 4,34 0,23 0,85 9 54 200 420 4,54 0,23 0,86 10 55 200 390 4,89 0,23 0,87
- 17. 17 1.10 GRAFIK a. Karakteristik Tanpa Beban Gambar 1.5 Karakteristik Tanpa Beban b. Karakteristik Hubung Singkat Gambar 1.6 Karakteristik Tanpa Beban 0 1 2 3 4 5 6 7 0 20 40 60 cospi,I(A),P(kW) VL (Volt) Karakteristik Tanpa Beban cos pi=f(V) I=f(V) P=f(V) Expon. (cos pi=f(V)) Expon. (I=f(V)) Expon. (P=f(V)) 0 10 20 30 40 50 60 70 80 90 100 0 2 4 6 8 Vhs(V),PhS(W),cospi Ihs (A) Karakteristik Hubung Singkat Vhs=f(Ihs) Phs=f(Ihs) cos pi=f(Ihs) Expon. (Vhs=f(Ihs)) Expon. (Phs=f(Ihs)) Expon. (cos pi=f(Ihs))
- 18. 18 c. Karakteristik Berbeban Gambar 1.6 Karakteristik Berbeban 1.10 KESIMPULAN 1. Dari grafik karakteristik hubung singkat diperoleh bahwa semakin besar Ihs maka Vhs dan Phs akan ikut membesar,dan juga nilai cos pi akan semakin turun jika daya motor naik 2. Pada gambar karakteristik beban nol diperoleh hubungan antara V0 dengan I0, dan cos ├ś. Dimana kenaikan V0 mengakibatkan I0 ikut membesar, sedangkan terhadap cos ├ś menurun dan Daya nilainya kecil atau jarak intervalnya berdekatan jadi bisa dikatakan konstan. 3. Dengan bertanbambahnya beban maka putaran motor akan turun yang mengakibantkan torsi ikut turun 0 500 1000 1500 2000 2500 3000 0 50 100 150 200 250 Putarann,(rpm) Daya P, (Watt) Karakteristik Berbeban n=f(P) Expon. (n=f(P))