狠狠撸

Temporal Regularized Matrix Factorization
for High-dimensional Time Series Prediction
Hsiang-Fu Yu*, Nikhil Rao**, Inderjit S. Dhillon*
*University of Texas at Austin
**Technicolor Research
発表者：林勝悟
NIPS2016読み会＠立命茨木
2017/03/18

自己紹介
? 発表者：林勝悟
現所属：阪大産業科学研究所沼尾研M2年
4月から：京大鹿島研D1
? 研究興味：異常検知?変化検知 in 構造データ
? 趣味：スケボー，日本茶
（南部鉄器で沸かしたお湯を，ガラスの茶海で冷まし，
常滑焼の急須で淹れ，有田焼の湯呑みで頂くのが直近
の夢）
2

時系列データ
? 高次元化する時系列データ
– 数千次元に上るデータの予測の計算コストは莫大
? ノイジーかつ欠損値が多い
? 高次元かつ欠損値にも対応できるモデルが必要
3
*1 https://climatedataguide.ucar.edu/climate-data/gpcp-monthly-global-precipitation-climatology-project
1979-2010年に観測された降雨量*1

既存時系列モデル
? Autoregressive (AR) Models
? Dynamic Linear Models
– e.g. Kalman filter
? 計算コストと欠損値の扱いが問題
– n次元T時系列データに対するL次 AR modelの
O(Ln^2)のパラメータ推定の計算オーダーは
O(TL^2n^4+L^
– Kalman filterはパラメータアップデートに
（kは潜在次元数）
– ARは欠損値扱いが困難[1]
4

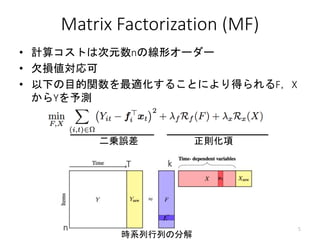
Matrix Factorization (MF)
? 計算コストは次元数nの線形オーダー
? 欠損値対応可
? 以下の目的関数を最適化することにより得られるF，X
からYを予測
5
二乗誤差正則化項
n
kT
時系列行列の分解

MFの時間正則のためのグラフ正則
6
グラフ
依存時系列差
集合(lag set)
エッジ重み
のグラフ

グラフ正則の問題
? のため逆相関を扱えない
? グラフ構造が自明なケースは少ない
– ＝{1} が多用されるが，予測精度に問題
– エッジ重みの学習が難しい
? 以下の最適化問題を解くと＝を得てしまう
? の正則化項を設けても，
＝1である，ワンホットベクトルを得て
しまう．ここで，
7

Temporal Regularized Matrix Factorization (TRMF)
著者らは時系列モデルに基づく正則化項の導入を提案
? データドリブンに時間構造を学習
? (既存MFと同様に)
– 欠損値対応可
– スケーラブル
? 既存ソルバーが適用可
? 逆相関も学習可
8

のある時系列モデルを想定
以下の正則化項をMFの目的関数に導入
9
ガウシアンノイズとをパラメータ
とする時系列モデル
(cont.)

? の目的関数はある種のMAP推定であるため，既存ア
ルゴリズムで適切に推定可能
? でを予測した後，
により，予測
? ＝で欠損値補間
10
(cont.2)

TRMF AR Models (TRMF-AR)
TRMFのARモデルを提案．
とする．ここで，
このとき，ARに基づく正則化項を以下の用に記述．
なお，，，
11

TRMF AR Models (TRMF-AR) (cont.)
をそれぞれ対角行列に制約．
– パラメータ数 →
– 過学習を回避
– 解釈性が向上
以降，列がの対角成分であり，それ以外の成分が
0であると表記．
以下のように正則化項を変形．
ここで，をのr行，
をのr行．
12

TRMF AR Models (TRMF-AR) (cont.2)
? がそれぞれ対角行列になっても，を通して，
の各次元間の構造学習が可能
（逆に言うと，潜在空間の各次元が他次元と独立なAR
となるようにを学習する）
? はドメイン知識を自由組み込んだり長期間に設定可
e.g. 1日単位のデータの季節周期
13

グラフ正則とTRMF-ARの関係
となるように，
，
とする．このとき，ある対角行列と重み符号
付きグラフが存在し，
となる．また，，において
，
である．
14
の場合のグラフ
定理１

TRMF-ARのパラメータ最適化
交互最適化法により最適化可能
各パラメータの計算コスト
?
Alternating Least SquaresやCoordinate Descentで
?
– Graph Regularizationと同じ形式で表現できるため，
GRALS[4]が適用可能で
?
フロベニウスノルムの場合，
コレスキー分解で，
15

既存Temporal MFとTRMF-ARの関係
TRMF-ARは既存Temporal MFの一般化に相当
? Temporal Collaborative Filtering[23]は
? Nonnegative Matrix Factorization[5]は，
を使って，
となる
? [6,7]はに対して
16

Gaussian Markov Random Fieldsと
TRMF-ARの関係
GMRF：
任意の，において，TRMF-ARに対応する
GMRFの共分散行列は，定理１のと同様の非対
角成分の非零パターンを持ち，
である．
17
e.g.
系１

TRMF-ARの関係 (cont.)
とすると，[4]のTheorem 1と系1より，
を用いて以下の重み付き核型ノルムを記述できる．
ここで，，である．
とするとき，以下の凸緩和問題(1)を考える．
ここで，，はlow spikiness[4]な行列集合である．
このとき，[4]のTheorem 2より，続く系2を得る．
18
???(1)

TRMF-ARの関係 (cont.2)
をランクで時系列の正解行列とす
る．を，分散のガウスノイズがのり，ランダムに
観測されである行列とする．凸緩和問題(1)で
得られた確信度の高いを用いて，
であり，が与えられている場合，
である．ここで，は正定数であり，はに
依存する．
19
系２

実験設定
データセットの統計
各手法の
kとλは時系列交差検証で決定し，Normalized Deviationと
Normalized Root Mean Squared Errorを評価 20
手法 synthetic electricity traffic walmart-1 walmart-2
TRMF-AR {1,…,8} {1,…,24}Ｕ{7×24,…,8×24-1} {1,…,10}Ｕ{50,…56}
SVD-AR(1) 1 1 1 1 1
TCF[23] 1 1 1 1 1
AR(1) 1 1 1 1 1
DLM 1 1 1 1 1
Mean all all all all all
synthetic electricity traffic walmart-1 walmart-2
n 16 370 963 1,350 1,582
T 128 26,304 10,560 187 187
欠損比 0% 0% 0% 55.3% 49.3%

スケーラビリティの実験結果
? n=50000では，2オーダー早い
21
(T=512)

予測の実験結果
22
Matrix Factorization Models Time Series Models
TRMF-AR SVD-AR(1) TCF AR(1) DLM R-DLM Mean
synthetic 0.373/0.487 0.444/0.872 1.000/1.424 0.928/1.401 0.936/1.391 0.996/1.420 1.000/1.424
electricity 0.255/1.397 0.257/1.865 0.349/1.838 0.219/1.43
9
0.435/2.753 -/- 1.410/4.528
traffic 0.187/0.423 0.555/1.194 0.624/0.931 0.275/0.536 0.639/0.951 -/- 0.560/0.826
walmart-1 0.533/1.958 -/- 0.540/2.231 -/- 0.602/2.293 -/- 1.239/3.103
walmart-2 0.432/1.065 -/- 0.446/1.124 -/- 0.453/1.110 -/- 1.097/2.088
欠損値なしデータ
欠損値ありデータ

欠損値補間の実験結果
23
ある割合のデータを欠損値として予測

結論
? 著者らは，欠損値を含む高次元データにも有効な
Temporal Regularized Matrix Factorization(TRMF)及びARに
基づくTRMF-ARを提案
? TRMFは自動で時間依存性を学習
? TRMF-ARと既存研究を関連付けた
? 高いスケーラビリティと精度を実証
24

レビュー
５ 2-Confident (read it all; understood it all reasonably well)
１ 1-Less confident (might not have understood significant
parts)
6レビュー全て割りとべた褒めで，提案や論文構成に対
するネガティブなコメントは特に無し
25

コメント
Pros
? 論文構成や既存研究との関連付けが綺麗
Cons
? AR(7)等の予測精度と比較?議論すべきでは？比較手法
が提案法に多少都合の良いように設定された印象
? 逆相関を持つ人工データも実験すればもっと提案法の
主張を強められたのでは？
26

参考文献
[1] O. Anava, E. Hazan, and A. Zeevi. Online time series prediction with missing data. In
Proceedings of the International Conference on Machine Learning, pages 2191–2199, 2015.
[3] L. Xiong, X. Chen, T.-K. Huang, J. G. Schneider, and J. G. Carbonell. Temporal collaborative
filtering with Bayesian probabilistic tensor factorization. In SIAM International Conference on Data
Mining, pages 223–234, 2010.
[4] N. Rao, H.-F. Yu, P. K. Ravikumar, and I. S. Dhillon. Collaborative filtering with graph information:
Consistency and scalable methods. In Advances in Neural Information Processing Systems 27, 2015.
[5] Z. Chen and A. Cichocki. Nonnegative matrix factorization with temporal smoothness and/or
spatial decorrelation constraints. Laboratory for Advanced Brain Signal Processing, RIKEN, Tech.
Rep, 68, 2005.
[6] M. Roughan, Y. Zhang, W. Willinger, and L. Qiu. Spatio-temporal compressive sensing and
internet traffic matrices (extended version). IEEE/ACM Transactions on Networking, 20(3):662–676,
June 2012.
[7] Y. Zhang, M. Roughan, W. Willinger, and L. Qiu. Spatio-temporal compressive sensing and
internet traffic matrices. SIGCOMM Comput. Commun. Rev., 39(4):267–278, Aug. 2009. ISSN 0146-
4833.
27

予備
? [3]
? Spikiness[4] ：
?
?
28

狠狠撸

第３回関西NIPS読み会：Temporal Regularized Matrix Factorization for High dimensional Time Series Prediction

More Related Content

第３回関西NIPS読み会：Temporal Regularized Matrix Factorization for High dimensional Time Series Prediction