Nombres Enters
- 2. Nombres enters Els nombres naturals, el zero i els nombres negatius Ordenaci坦 de nombres enters Suma i resta de nombres enters Multiplicaci坦, divisi坦 i pot竪ncia denters
- 3. Nombres enters Els nombres naturals, el zero i els nombres negatius Els naturals, els decimals i les fraccions s坦n conjunts de nombres que ens indiquen el resultat de comptar elements o de mesurar magnituds referides a una unitat.
- 4. Nombres enters L1, el 2, el 25 i el 498 s坦n exemples de nombres naturals. Els nombres naturals s坦n els enters (no decimals) i positius. Sescriuen sense cap signe. Per resoldre operacions, els matemtics han hagut dampliar el conjunt dels nombres naturals: shi afegeix el zero i els nombres negatius i sobt辿 el conjunt dels nombres enters. {naturals + zero + enters negatius} = conjunt dels enters Els nombres naturals
- 5. Nombres enters Els nombres negatius El 3, el 57 i el 708 s坦n exemples de nombres negatius. Els nombres negatius s坦n els enters (no decimals) i negatius. Sescriuen amb un signe menys al davant.
- 6. Nombres enters El zero El zero no 辿s ni positiu ni negatiu. Sescriu sense cap signe. En algunes situacions de la vida quotidiana apareixen nombres positius, negatius i el zero: Temperatures Altitud Extracte bancari Liceberg com a s鱈mil del positiu, el negatiu i el zero
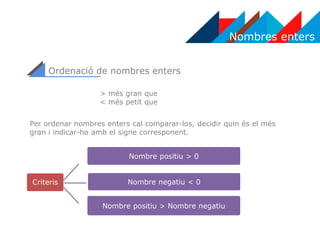
- 7. Nombres enters Ordenaci坦 de nombres enters > m辿s gran que < m辿s petit que Per ordenar nombres enters cal comparar-los, decidir quin 辿s el m辿s gran i indicar-ho amb el signe corresponent. Criteris Nombre positiu > 0 Nombre negatiu < 0 Nombre positiu > Nombre negatiu
- 8. Nombres enters Valor absolut El valor absolut dun nombre enter 辿s el nombre que en resulta quan se suprimeix el seu signe. Sindica amb dues barres verticals: |51| = 51. Criteris Entre dos de positius, 辿s m辿s gran el de valor absolut m辿s gran: 16 > 5. Entre dos de negatius, 辿s m辿s gran el de valor absolut m辿s petit: 10 > 34. Els nombres enters es poden representar sobre una recta num竪rica. Sordenen de petit a gran desquerra a dreta, amb els nombres negatius a lesquerra del zero i els positius a la dreta.
- 9. Nombres enters Suma de nombres enters Entre dos nombres enters es poden efectuar les mateixes operacions que entre dos nombres naturals. Dos enters positius Dos enters negatius Dos enters de signe diferent Se sumen els valors absoluts i el resultat 辿s positiu: 4 + 3 = 7 Se sumen els valors absoluts i el resultat 辿s negatiu: 4 + (3) = 7 Es resten els valors absoluts i el resultat 辿s el del sumand de valor absolut m辿s gran: 4 + 3 = 1 La suma de nombres enters verifica les propietats commutativa, associativa, element neutre i oposat dun nombre enter.
- 10. Nombres enters Resta de nombres enters Dos enters positius Dos enters negatius Dos enters de signe diferent Minuend < Subtrahend restem valors absoluts, resultat negatiu 5 8 = 3 Comparem valors absoluts: Minuend > Subtrahend resultat negatiu 6 (5) = 1 Minuend < Subtrahend resultat positiu 2 (11) = 9 La resta de dos nombres enters 辿s loperaci坦 inversa de la suma. Minuend > Subtrahend restem valors absoluts, resultat positiu 6 2 = 4 Minuend positiu subtrahend negatiu, sumem valors absoluts, resultat positiu 2 (4) = 6 Minuend negatiu, subtrahend positiu sumem valors absoluts, resultat negatiu 1 7 = 8 Minuend subtrahend = resultat
- 11. Nombres enters Multiplicaci坦 de nombres enters La multiplicaci坦 de dos nombres enters sempre t辿 com a resultat un altre nombre enter. El valor absolut del producte 辿s la multiplicaci坦 del valor absolut dels factors. Per saber el signe del resultat, cal seguir la regla dels signes: Factors del mateix signe: resultat positiu Factors de signe diferent: resultat negatiu La multiplicaci坦 de nombres enters verifica les propietats commutativa, associativa, element unitat i distributiva. +揃+ = + 揃 = + +揃 = 揃+ =
- 12. Nombres enters Divisi坦 de nombres enters + : + = + : = + + : = : + = La divisi坦 exacta de dos nombres enters 辿s loperaci坦 inversa de la multiplicaci坦. Dividend Divisor Residu = 0 Quocient Cal dividir el valor absolut del dividend entre el valor absolut del divisor. Per saber el signe del resultat, cal seguir la regla dels signes.
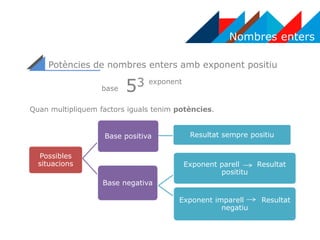
- 13. Nombres enters Pot竪ncies de nombres enters amb exponent positiu Quan multipliquem factors iguals tenim pot竪ncies. Possibles situacions Base positiva Base negativa Exponent parell Resultat posititu Exponent imparell Resultat negatiu Resultat sempre positiu 53base exponent