狈笔完全问题の绍介
- 4. はじめに ? ??完全問題どれぐらい知ってますか? ? ???、頂点被覆問題、ハミルトンパス問題、 部分和問題、巡回セールスマン問題、 ナップザック問題 ???. ? 頂点被覆、部分和問題について紹介します
- 6. モチベーション ? ??完全はなぜ定義する? ? ?? = ?を示すときに役立つ
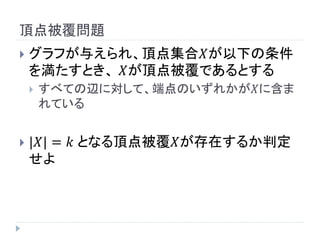
- 7. 頂点被覆問題 ? グラフが与えられ、頂点集合?が以下の条件 を満たすとき、 ?が頂点被覆であるとする ? すべての辺に対して、端点のいずれかが?に含ま れている ? |?| = ? となる頂点被覆?が存在するか判定 せよ
- 8. 復習 ? 言語?が??完全であることを示すためには以 下が必要十分 ? ?が??に属する ? ??に属する任意の言語?が、?に多項式時間で帰 着可能
- 13. 作り方(具体例) ? ????? ? ????? という3???を考える ? これは変数が?(= 3)個あり、節が?(= 2)個あ るので、次ページのような 2? + 3? 頂点のグ ラフにサイズ ? + 2? の頂点カバーがあるか どうかに帰着される
- 14. グラフ
- 15. 確認 ? 3??? ∶ ? = ????, ? = ????, ? = ?????で成立 ? サイズ7(= ? + 2?)の頂点被覆は次頁のよう に確かに存在する ? よって、成立
- 16. グラフ
- 17. 構成方法-頂点 ? 各変数?に対して、 ? 2頂点作る ? ?と?に対応させる ? 各節s????に対して、 ? 3頂点作る ? s, ?, ?に対応させる
- 18. 構成方法-辺 ? 各変数?に対して、 ? ?と?に対応する辺の間に辺を引く ? 各節s????に対して、 ? 3頂点をそれぞれ対応する文字の頂点に辺を張 る ? 3頂点の任意の2点間に辺を張る
- 19. グラフ ? ??? ? ? ? ? ? ? ? ?
- 20. グラフ ? ??? ? ? ? ? ? ? ? ?
- 21. グラフ ? ??? ? ? ? ? ? ? ? ?
- 22. 正当性 ? グラフがサイズ? + 2?の頂点被覆を持つ ?3???が????になる ? まず、 を示す
- 23. 正当性 ? グラフがサイズ? + 2?の頂点被覆を持つとき ? ?と?に対応する頂点から少なくとも1つ選ぶ ? 節s????に対して、少なくとも2つ選ぶ ? 必要がある(easy)
- 24. 正当性 ? 頂点被覆のサイズの下限が? + 2?で、等号 が成立 ? ?と?に対応する頂点からちょうど1つ選ぶ ? 節s????に対して、ちょうど2つ選ぶ
- 25. 正当性 ? よって、各変数に対して?と?で選ばれた方が ????となるように真偽を定める ? こうすれば、3???が満たされる ? みなさん考えてみてください
- 26. 正当性 ? グラフがサイズ? + 2?の頂点被覆を持つ ?3???が????になる ? 次に、 を示す
- 27. 正当性 ? グラフがサイズ? + 2?の頂点被覆を持つ ?3???が????になる ? 次に、 を示す ? これは同じように3???の解に対応する頂点を 選び、節に対応する頂点を適当に選べばよい
- 28. 部分和問題 ? 数列?1, ?2, … ? ?から何個か選んで合計を?に できるかどうか判定 ? 3???が????になる条件をこれに帰着する
- 29. 部分和問題 ? うまく帰着できる形に変形する ? 変数?に対して?と?に対応する文字を導入す る ? 文字の値を、対応する変数が????の時+1、 ?????の時+0として条件を調べる
- 30. 部分和問題 ? 変数?に対して?と?のいずれかを選ぶからこ れらに対応する文字の和は1 ? 節s????に対して、 s, ?, ?に対応する文字の 和は1以上3以下
- 31. 部分和問題 ? 変数?に対して?と?のいずれかを選ぶからこ れらに対応する文字の和は1 ? 節s????に対して、 s, ?, ?に対応する文字の 和は1以上3以下 ? 等号の式にするために補助的な変数を導入する
- 32. 部分和問題 ? 節s????に対して、 s, ?, ?に対応する文字の 和は1以上3以下 ? よって、各節に対して新しい文字を二つ作る ? これによって、0~2まで足すことができる ? このとき、合計を3にできるのが条件
- 33. 部分和問題 ? 条件を一列に並べよう ? 例として (? ∨ ?)に対応する部分和問題を構 成する(節の名前を?1とする)
- 36. 部分和問題 ? ? ? ? ?1 ?1 sum 1 1 1 1 1 1 1 1 1 1 3 0 0 0 0 0 0 0 0 0 0 100 101 10 10 1 1 113
- 37. 部分和問題 ? ? ? ? ?1 ?1 sum 1 1 1 1 1 1 1 1 1 1 3 0 0 0 0 0 0 0 0 0 0 100 101 10 10 1 1 113 これに対して部分和 問題を解けば同値
- 39. おわりに ? 少したくさん話しました ? 雰囲気でも分かってもらえたらうれしいです ? ご清聴ありがとうございました