Numerical Methods
?Download as DOCX, PDF?
0 likes?583 views
This document contains summaries of several chapters from a numerical methods textbook. It discusses various numerical techniques for solving equations including bracketing methods, bisection method, false position method, fixed point iteration, Newton's method, secant method, and systems of nonlinear equations. It also covers numerical integration techniques like Trapezoidal rule, Simpson's rule, Newton-Cotes formulas, Romberg integration and Gaussian quadrature. Finally, it summarizes chapters on interpolation, least squares regression, and Runge-Kutta methods for solving differential equations.
Numerical Methods
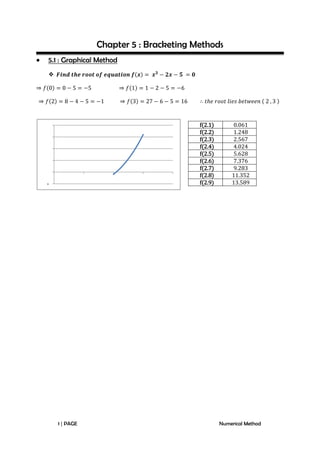
- 1. Chapter 5 : Bracketing Methods 5.1 : Graphical Method f(2.1) f(2.2) f(2.3) f(2.4) f(2.5) f(2.6) f(2.7) f(2.8) f(2.9) - 1 PAGE 0.061 1.248 2.567 4.024 5.628 7.376 9.283 11.352 13.589 Numerical Method
- 2. 5.2 : Bisection Method ? 3 ways to stop iteration : 1- Result of function a or b ? zero 2- Two X's should equal to each other 3- Error = zero or 10 % ( depend on question ) 2 PAGE Numerical Method
- 3. 5.2 Page 139 : Iteration 1 2 3 4 5 3 PAGE 0 0 0.25 0.375 0.438 1 0.5 0.5 0.5 0.5 0.5 0.25 0.375 0.438 0.469 0.2 -0.868 -0.308 -0.049 0.076 -----0.5 0.25 0.375 0.438 -----100 % 33.333 % 14.385 % 6.610 % Numerical Method
- 4. 5.3 : False-Position Method or Rugula Falsi or Linear Interpolation Method : C C C 5.11 Page 139 : Iteration 1 2 3 4 5 6 7 8 9 10 2 2.768 3.177 3.364 3.443 3.476 3.489 3.494 3.496 3.497 4 PAGE -68.686 -44.716 -22.844 -10.177 -4.268 -1.728 -0.660 -0.270 -0.106 -0.045 5 5 5 5 5 5 5 5 5 5 199.508 199.508 199.508 199.508 199.508 199.508 199.508 199.508 199.508 199.508 2.768 3.177 3.364 3.443 3.476 3.489 3.494 3.496 3.497 3.497 -44.716 -22.844 -10.177 -4.268 -1.728 -0.660 -0.270 -0.106 -0.045 -----2.768 3.177 3.364 3.443 3.476 3.489 3.494 3.496 -----12.874 % 5.559 % 2.295 % 0.949 % 0.373 % 0.143 % 0.057 % 0.029 % Numerical Method
- 5. Chapter 6 : Open Methods 6.1 : Simple Fixed Method Iteration Method or Method Successive Approximation ? ? 5 PAGE ? Numerical Method
- 7. ? ? Iteration 1 2 3 4 5 6 7 8 9 10 11 12 7 PAGE 0.5 0.585 0.526 0.567 0.538 0.558 0.544 0.554 0.547 0.552 0.549 0.551 0.585 0.526 0.567 0.538 0.558 0.544 0.554 0.547 0.552 0.549 0.551 0.549 -----11.217 % 7.231 % 5.390 % 3.584 % 2.574 % 1.805 % 1.280 % 0.906 % 0.546 % 0.363 % 0.364 % Numerical Method
- 8. 6.2 : Newton's Raphson Method -----0 1 2 3 8 PAGE -----0.5 0.714 0.683 0.682 -0.375 0.078 0.002 -0.001 1.750 2.529 2.399 2.395 3 4.284 4.098 4.092 Numerical Method
- 9. 6.3 : The Secant Method ------1 0 1 2 3 -----1.9 1.557 1.509 1.5 1.5 -0.960 -0.117 -0.018 0 -2.8 -2.114 -2.018 -2 6.2 Page 171 : C ) by Newton's Raphson Method : ----- -----0 3 9 PAGE -3.2 1.5 3.6 Numerical Method -----------
- 10. 1 2 3 4 5 6 7 5.133 4.270 3.793 3.6 3.564 3.563 3.563 48.072 12.963 2.949 0.4 0.009 -0.002 55.674 27.179 15.264 11.22 10.515 10.496 38.196 27.840 22.116 19.8 19.368 19.346 1.029 0.527 0.382 0.337 0.347 0.320 D ) by Secant Method : ------1 0 1 2 3 4 5 -----3 4 3.327 3.481 3.586 3.561 3.563 -3.2 6.6 -1.966 -0.798 0.245 -0.023 -0.002 ----------25 % 20.228 % 4.424 % 2.928 % 0.702 % 0.056 % 6.9 Page 172 : B ) by Newton's Raphson Method : ----0 1 2 3 -----3.5 3.366 3.345 3.345 0.606 0.072 0.001 4.513 3.472 3.318 8.150 7.386 7.267 ----------13.030 185.925 C ) by Secant Method : ------1 0 1 2 3 4 5 6 7 10 PAGE -----2.5 3.5 3.063 3.292 3.367 3.343 3.344 3.345 3.345 -0.781 0.606 -0.667 -0.165 0.076 -0.005 -0.002 0.001 ----------28.571 % 14.267 % 6.956 % 2.228 % 0.718 % 0.030 % 0.030 % Numerical Method
- 11. 6.6 : The System of non linear equations 11 PAGE Numerical Method
- 13. Chapter 21 : Newton-Cotes Integration Formulas 21.1 : Trapezoidal Rule X 4 0.25 4.2 0.238 4.4 0.227 4.6 0.217 4.8 0.208 5 0.2 5.2 0.192 0.2 3.030 0.4 2.798 0.6 2.898 0.8 3.166 1 3.560 1.2 4.070 1.4 4.704 Y X Y 13 PAGE Numerical Method
- 14. 21.2 : Simpson's Rule 1) 2) X 4 0.25 4.2 0.238 4.4 0.227 4.6 0.217 4.8 0.208 5 0.2 5.2 0.192 0.2 3.030 0.4 2.798 0.6 2.898 0.8 3.166 1 3.560 1.2 4.070 1.4 4.704 Y X Y 14 PAGE Numerical Method
- 15. 21.3 : Integration With Un Equal Segments 21.13 Page 628 : X 0 2 0.05 1.8555 0.15 1.5970 0.25 1.3746 0.35 1.1831 0.475 0.9808 0.6 0.8131 Y A ) by Analytical mean : A ) Consider equal interval problem using trapezoidal rule with 8 intervals : X 0 0 0.5 0.632 1 0.865 1.5 0.950 2 0.982 2.5 0.993 3 0.998 3.5 0.999 4 1 Y B ) Consider un equal interval problem : X 0 0 0.1 0.5 0.181 0.632 1.2 0.909 1.4 0.939 2 0.982 2.8 0.996 2.9 0.997 3.2 3.8 0.998 0.999 Y 15 PAGE Numerical Method 4 1
- 16. C ) Check your answer by exact value : 16 PAGE Numerical Method
- 17. Chapter 22 : Integration of Equations 22.1 : Newton's Cotes Algorithms of Equations 17 PAGE Numerical Method
- 18. 22.2 : Romberg Integration X 0 1 0.5 0.667 1 0.5 Y X 0 1 0.25 0.8 0.5 0.667 0.75 0.571 1 0.5 Y X 0 1 0.125 0.889 0.25 0.8 0.375 0.727 0.5 0.667 0.625 0.615 0.75 0.571 0.875 0.533 1 0.5 Y 18 PAGE Numerical Method
- 20. 22.4 : Gauss Quadrature 22. 3 Page 651 : 20 PAGE Numerical Method
- 22. Chapter 18 : Interpolation and Extrapolation 18.1 : Newton's Divided Differences Interpolating Polynomials Un equal intervals X 1 19 20 25 30 Y X 0 1 2 3 5 20 25 7 30 X 2 3 12 147 Y X 0 2 1 2 5 12 147 22 PAGE Numerical Method
- 24. 18.2 : Lagrange Interpolating Polynomials X 4 3 24 39 Y 24 PAGE Numerical Method
- 25. 18.4 : Inverse Interpolation X 6 24 58 108 18 10 -18 174 90 Y X Y 25 PAGE Numerical Method
- 26. Chapter 17 : Least-Square Regression 17.1 : Linear Regression 10 2 3 4 42 58 a) b) c) 1 10 10 1 3 4 42 58 126 232 9 16 26 PAGE -3.6 6.3 -1.8 -0.9 12.96 39.69 3.24 0.81 Numerical Method
- 28. 17.2 : Polynomial Regression a) b) c) 1.6 4 4 7 4.4 3.4 3 1.6 4.8 9 5 7 4.4 3.4 22 23.8 25 49 Matrix in Calculator 28 PAGE Mode 14.4 57.6 110 166.6 14.4 64 125 343 81 256 625 2401 5 : Equ 2: anX+bnY+cnZ=dn Numerical Method
- 29. Chapter 25 : Runge-Kutta Methods 25.1 : Euler's Method X 0 0.4 1.003 2.203 4.009 8.306 Y 29 PAGE Numerical Method
- 30. Modified Euler's Method X 0 0.805 -0.264 1 1.875 2.811 Y X Y 30 PAGE Numerical Method
- 31. 25.2 : Improvement of Euler's Method X 1 1.526 2.109 Y 31 PAGE Numerical Method
- 32. 25.3 : Runge-Kutta Method Second order X 2 2.205 2.421 2.109 Y 32 PAGE Numerical Method