Numerical solutions of algebraic equations
- 1. SEMINAR On engineering mathematics TOPIC: NUMERICAL SOLUTION OF ALGEBRAIC EQUATIONS AVNEET SINGH LAL EC-2
- 2. SOLUTION OF ALGEBRAIC AND TRANSCENDENTAL EQUATIONS ŌĆó Consider the equation of the form f(x)=0. ŌĆó If f(x) is a quadratic, cubic or biquadratic expression then algebraic formulae are available for expressing the roots. ŌĆó But when f(x) is a polynomial of higher degree or an expression involving transcendental functions e.g., 1 + cos x ŌĆō 5x, x tan x ŌĆō cosh x, e-x ŌĆō sin x etc., algebraic methods are not available.
- 3. METHODS In order to solve these type of equations following methods exist: ŌĆó DIRECTIVE METHODS: The methods which are used to find solutions of given equations in the direct process is called as directive methods. Example: remainder theorem, Factorization method etc Note: By using Directive Methods, it is possible to find exact solutions of the given equation. ŌĆó ITERATIVE METHODS (INDIRECT METHODS): The methods which are used to find solutions of the given equation in some indirect process is called as Iterative Methods Note: By using Iterative methods, it is possible to find approximate solution of the given equation and also it is possible to find single solution of the given equation at the same time.
- 4. DESCARTES RULE OF SIGNS ŌĆó Number of positive roots of f(x) = 0 is equal to the number of sign changes of the coefficients or is less than this number by an even integer. ŌĆó The number of negative roots of f(x) = 0 is obtained by considering the number of sign changes in f(ŌĆōx). ŌĆó EXAMPLE: f (x) = x5 + 2x4 ŌĆō 5x3 ŌĆō 7x2 + 12x + 2 No. of sign change = 2 = Positive Roots f (-x) = ŌĆō x5 + 2x4 + 5x3 ŌĆō 7x2 ŌĆō 12x + 2 No. of sign change = 3 = Negative Roots
- 5. ITERATIVE METHODS ŌĆó BISECTION METHOD ŌĆó REGULA FALSI ŌĆó NEWTON RAPHSON
- 6. BISECTION METHOD ŌĆó This method is based on the repeated application of intermediate value property. ’ü▒ Locate the interval (a, b) in which root lies. ’ü▒ Bisect the interval (a, b). ’ü▒ Choose the half interval in which the root lies. ’ü▒ Bisect the half interval. ’ü▒ Repeat the process until the root converges.
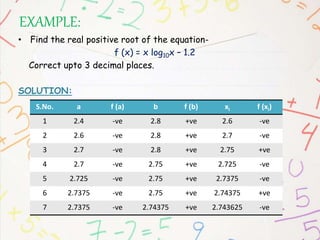
- 7. EXAMPLE: ŌĆó Find the real positive root of the equation- f (x) = x log10x ŌĆō 1.2 Correct upto 3 decimal places. SOLUTION: S.No. a f (a) b f (b) xi f (xi) 1 2.4 -ve 2.8 +ve 2.6 -ve 2 2.6 -ve 2.8 +ve 2.7 -ve 3 2.7 -ve 2.8 +ve 2.75 +ve 4 2.7 -ve 2.75 +ve 2.725 -ve 5 2.725 -ve 2.75 +ve 2.7375 -ve 6 2.7375 -ve 2.75 +ve 2.74375 +ve 7 2.7375 -ve 2.74375 +ve 2.743625 -ve
- 8. REGULA FALSI METHOD ŌĆó This is the oldest method for finding the real roots of a numerical equation. ŌĆó It is sometimes known as method of linear interpolation. ’ü▒ Locate the interval (a, b) in which the root lies. ’ü▒ First Approximation to the root ’ü▒ Locate the next interval (a, X0) or ( X0, b ) in which root lies. ’ü▒ Repeat the process until the root converges.
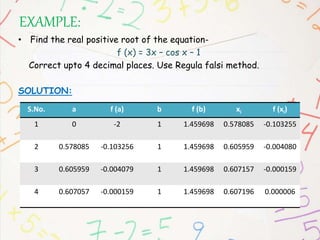
- 9. EXAMPLE: ŌĆó Find the real positive root of the equation- f (x) = 3x ŌĆō cos x ŌĆō 1 Correct upto 4 decimal places. Use Regula falsi method. SOLUTION: S.No. a f (a) b f (b) xi f (xi) 1 0 -2 1 1.459698 0.578085 -0.103255 2 0.578085 -0.103256 1 1.459698 0.605959 -0.004080 3 0.605959 -0.004079 1 1.459698 0.607157 -0.000159 4 0.607057 -0.000159 1 1.459698 0.607196 0.000006
- 10. NEWTON RAPHSON METHOD ŌĆó This method is generally used to improve the result obtained by one of the previous methods. ’ü▒ Locate the interval (a, b). ’ü▒ Choose a or b which is nearer to the root as the first approximation x0 to the root. Next approximation: ’ü▒ Repeat the process until the root converges.
- 11. EXAMPLE: ŌĆó Find a positive value of (17)1/3 correct to six decimal places by Newton Raphson method. SOLUTION: The root lies between 2.5 and 2.6. Since, |f (2.6)| < |f (2.5)| Therefore, the root is nearer to 2.6. Let us take x0 = 2.58. Putting n = 0, 1, 2, ..., successively in Newton RaphsonŌĆÖs formula, we get- x1 = 2.571311 x2 = 2.571281 x3 = 2.5712815 Since x2 and x3 are same up to 6 decimal places, hence, the required Positive root is 2.571281.
- 12. ORDER OF CONVERGENCE OF ITERATIVE METHODS ŌĆó The order of convergence is the order at which the error between two successive approximation to the root decreases. ŌĆó Where: A is a non-zero finite number called asymptotic error constant. ei and ei+1 are the errors in successive approximations. k is the largest positive real number
- 13. REFERENCES ŌĆó ENGINEERING MATHEMATICS ( N.P. BALI) ŌĆó http://www.sakshieducation.com/Engg/Engg Academia/CommonSubjects/MM- Algebraic&TransdentialEquations.pdf
- 14. !!!THE END!!! THANK YOU FOR YOUR ATTENTION