One dimensional problems
Download as PPTX, PDF
2 likes1,745 views
This document discusses one-dimensional finite element analysis problems. It covers types of elements including simplex and higher order elements. Common one-dimensional elements include line elements, rods, beams, trusses and frames. It also discusses node numbering schemes, boundary conditions including essential and natural boundary conditions, shape functions, and interpolation functions used to approximate behavior within an element.
One dimensional problems
- 1. One Dimensional Problems in FEA PRESENTED BY P.SIVASUBRAMANIYAN AP/MECH, KCET.
- 2. Types of Elements Simplex Elements (Having Primary nodes) Higher order elements (having primary and secondary nodes)
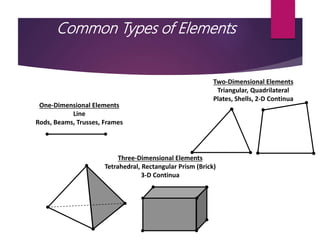
- 3. Common Types of Elements One-Dimensional Elements Line Rods, Beams, Trusses, Frames Two-Dimensional Elements Triangular, Quadrilateral Plates, Shells, 2-D Continua Three-Dimensional Elements Tetrahedral, Rectangular Prism (Brick) 3-D Continua
- 4. Location of Nodes Optional Essential
- 5. No of Elements Elements to be chosen related to the accuracy desired. Size Number of DOF
- 6. Node Numbering Scheme Maximum node number Minimum node number = Minimum Shorter side node numbering is better than Longer side
- 7. M/c component is loaded, displacement occur at various parts of the component. These displacement of various parts are known as DOF
- 9. Boundary Conditions F Geometric or Essential BC 1 2 Natural or Optional BC
- 10. Functions Finite Element Equation (Displacement at primary nodes) Shape Functions (Displacement at other locations in terms of primary nodal displacements)
- 11. Coordinate systems Global Local
- 12. Interpolation Functions The function used to represent the behaviour of the solution within an element is called interpolation function or approximate function. Polynomial Trignometric
- 13. Linear elements 个 = a1 + a2X Higher order (or) Non linear element 个 = a1 + a2x +a3 x2+ . Complex element Simplex element