One way anova
- 1. ONE WAY ANOVA I. Prinsip Dasar dan Tujuan Analisis Analisis ragam atau analysis of variance(ANOVA) adalah suatu metode untuk menguraikan keragaman total data menjadi komponen-komponen yang mengukur berbagai sumber keragaman. Secara aplikatif, ANOVA digunakan untuk menguji rata-rata lebih dari dua sampel berbeda secara signifikan atau tidak. II. Format Data Dasar dan Program Komputer yang Digunakan Program komputer yang dapat digunkan untuk ANOVA antara lain adalah SPSS. Data yang dimasukkan ke SPSS hanya terdiri dari dua kolom seperti ilustrasi tabel berikut ini: Tabel 2.1 Format Data ANOVA untuk SPSS Rata-rata Populasi … 1 … 1 … . … . … . … k III. Model Matematis dan Algoritma Pokok Analisis Misal ada sebanyak k populasi. Masing-masing populasi diambil sampel sebanyak n. Diasumsikan k populasi itu saling bebas dan mengikuti sebaran normal dengan parameter µ1, µ2, …, µk dan ragam sama σ2. k n T..2 Sum Squares Total = Σ Σ x ij − 2 i =1 j=1 nk ∑T 2 i. T..2 Sum Squares Between Groups = i − n n
- 2. Sum Squares Within Grous atau Sum Squares Error = SS Total-SS Between Groups xij adalah observasi ke-j dari populasi ke-i. Ti. adalah total semua observasi dalam sampel dari populasi ke-i, dan T.. adalah total semua nk observasi. Setiap observasi dapat ditulis dalam bentuk: xij=µij + εij εij adalah simpangan observasi ke-j dalam sampel ke-i dari rata-rta populasi ke-i. IV. Struktur Informasi Pokok Analisis 1. Deskripsi rata-rata dan standar deviasi dari sampel Dilihat dari tabel Descritives. 2. Uji homoskedastisitas Ho: varians k populasi sama H1: hipotesis nol tidak berlaku Lihat bagian Test of Homogeneity of Variances. 3. Hasil uji beda rata-rata k populasi (Ho: µ1= µ2= …= µk=0) Interpretasi dari tabel Anova. 4. Jika pada point 3 menghasilkan keputusan tolak Ho, tentunya kita ingin tahu populasi mana saja yang berbeda rata-ratanya secara signifikan. Utuk itu, lihat Post Hoc Test. 5. Berlawanan dengan point 4, jika kita ingin melihat populasi mana saja yang tidak berbeda secara signifikan, bisa dilihat pada Homogeneous Subset. V. Contoh Aplikasi Analisis Di sebuah fakultas pertanian diadakan penelitian untuk mengetahui apakah ada perbedaan pengaruh pemberian pupuk A, pupuk B, dan pupuk C pada pertambahan lebar daun tumbuhan X. Untuk itu, diambil sampel sebanyak 30, dibagi menjadi 3 kelompok. Masing-masing kelompok diberi pupuk yang berbeda. Hasilnya dapat dilihat pada tabel berikut ini:
- 3. Tabel 5.1 Data Pertambahan Lebar Daun Tumbuhan X Menurut Jenis Pupuk yang Diberikan (dalam cm) Pupuk A Pupuk B Pupuk C 4.9892 8.0173 14.0025 4.9873 7.996 13.9867 4.9995 7.9975 13.9965 5.0093 8.0029 13.9913 5.0045 8.0014 14.0048 4.9932 7.9818 13.981 5.0002 8.0066 14.001 5.0014 7.9954 14.0032 4.9982 8.0185 14.0157 5.0166 7.9834 14.0014 Sumber: Data Bangkitan dari Minitab Data di atas akan dianalisis dengan ANOVA. Format data ketika dientry ke SPSS harus diubah seperti format pada bagian II di atas. Untuk jelasnya, silakan lihat file One Way Anova pada SPSS. Untuk melakukan analisis ragam satu arah (ANOVA) dengan SPSS, berikut ini diberikan langkah-langkahnya: 1. Pada menu Analyze, pilih submenu Compare Means. Lalu pilih One Way Anova… 2. Setelah itu akan muncul kotak dialog. Gambar 5.1 Kotak Dialog Utama One Way Anova Bagian Dependent List diisi dengan variabel lebar daun (berupa data kuantitatif), dan Factor diisi dengan pupuk (data kualitatif). Untuk bagian Post Hoc, aktifkan Bonferroni dan Tukey. Pada bagian Options, aktifkan Descriptives dan Homogeneity of Variances. Sampai di sini pengisisan kotak dialog selesai.
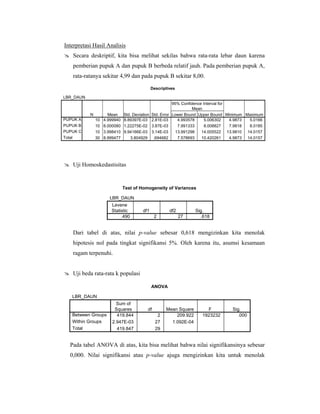
- 4. Interpretasi Hasil Analisis Secara deskriptif, kita bisa melihat sekilas bahwa rata-rata lebar daun karena pemberian pupuk A dan pupuk B berbeda relatif jauh. Pada pemberian pupuk A, rata-ratanya sekitar 4,99 dan pada pupuk B sekitar 8,00. Descriptives LBR_DAUN 95% Confidence Interval for Mean N Mean Std. Deviation Std. Error Lower Bound Upper Bound Minimum Maximum PUPUK A 10 4.999940 8.89397E-03 2.81E-03 4.993578 5.006302 4.9873 5.0166 PUPUK B 10 8.000080 1.22275E-02 3.87E-03 7.991333 8.008827 7.9818 8.0185 PUPUK C 10 13.998410 9.94166E-03 3.14E-03 13.991298 14.005522 13.9810 14.0157 Total 30 8.999477 3.804929 .694682 7.578693 10.420261 4.9873 14.0157 Uji Homoskedastisitas Test of Homogeneity of Variances LBR_DAUN Levene Statistic df1 df2 Sig. .490 2 27 .618 Dari tabel di atas, nilai p-value sebesar 0,618 mengizinkan kita menolak hipotesis nol pada tingkat signifikansi 5%. Oleh karena itu, asumsi kesamaan ragam terpenuhi. Uji beda rata-rata k populasi ANOVA LBR_DAUN Sum of Squares df Mean Square F Sig. Between Groups 419.844 2 209.922 1923232 .000 Within Groups 2.947E-03 27 1.092E-04 Total 419.847 29 Pada tabel ANOVA di atas, kita bisa melihat bahwa nilai signifikansinya sebesar 0,000. Nilai signifikansi atau p-value ajuga mengizinkan kita untuk menolak
- 5. hipotesis nol pada tingkat signifikansi 5%. Artinya minimal ada satu di antara ketiga pupuk itu yang memberikan pertambahan lebar daun yang berbeda. Mengetahui pupuk mana yang pengaruhnya berbeda Multiple Comparisons Dependent Variable: LBR_DAUN Mean Difference 95% Confidence Interval (I) JENIS PUPUK (J) JENIS PUPUK (I-J) Std. Error Sig. Lower Bound Upper Bound Tukey HSD PUPUK A PUPUK B -3.000140* 4.67E-03 .000 -3.011725 -2.988555 PUPUK C -8.998470* 4.67E-03 .000 -9.010055 -8.986885 PUPUK B PUPUK A 3.000140* 4.67E-03 .000 2.988555 3.011725 PUPUK C -5.998330* 4.67E-03 .000 -6.009915 -5.986745 PUPUK C PUPUK A 8.998470* 4.67E-03 .000 8.986885 9.010055 PUPUK B 5.998330* 4.67E-03 .000 5.986745 6.009915 Bonferroni PUPUK A PUPUK B -3.000140* 4.67E-03 .000 -3.012066 -2.988214 PUPUK C -8.998470* 4.67E-03 .000 -9.010396 -8.986544 PUPUK B PUPUK A 3.000140* 4.67E-03 .000 2.988214 3.012066 PUPUK C -5.998330* 4.67E-03 .000 -6.010256 -5.986404 PUPUK C PUPUK A 8.998470* 4.67E-03 .000 8.986544 9.010396 PUPUK B 5.998330* 4.67E-03 .000 5.986404 6.010256 *. The mean difference is significant at the .05 level. Tabel di atas ini memberikan hasil pengujian parsial dua populasi. Dari sini kita dapat mengetahui pupuk mana yang akan memberikan pengaruh yang berbeda. Ternyata ketiga pupuk memberikan pengaruh yang berbeda-beda, terlihat dari munculnya tanda bintang pada semua jenis pupuk. Sebaliknya, untuk mengetahui pupuk mana yang tidak berbeda secara signifikan pengaruhnya dapat dilihat pada tabel berikut ini. LBR_DAUN Subset for alpha = .05 JENIS PUPUK N 1 2 3 Tukey HSDa PUPUK A 10 4.999940 PUPUK B 10 8.000080 PUPUK C 10 13.998410 Sig. 1.000 1.000 1.000 Means for groups in homogeneous subsets are displayed. a. Uses Harmonic Mean Sample Size = 10.000. Terlihat ketiga sampel terbagi ke dalam tiga subset, yang menunjukkan bahwa ketiga pupuk memang mempunyai perbedaan yang signifikan dalam pengaruhnya terhadap pertambahan lebar daun.
- 6. Catatan: Uji Tukey dan Bonferroni dengan Homogeneous Subset selalu saling melengkapi. -Tita Rosy- -Sri Mulyani-