P g integralequations
- 2. Integral equations ŌĆó Any equation where an unknown function, to be determined appears under one or more integral signs it can be called an integral equation. (if the derivatives of the function are involved it is called an integro -differential equation) ŌĆó The actual development of the theory of integral equations began only at the end of the Integral functions are such where unknown is only outside the integral sign 2
- 3. Classification of integral equations Fredholm equation of the first type b f x K x, t t dt a Fredholm equation of the second type b x f x K x, t t dt a 3
- 4. Classification of integral equations Volterra equation of the first type x f x K x, t t dt a Volterra equation of the second type x x f x K x, t t dt a 4
- 5. Classification of integral equations Limits of the integration fixed: Fredholm One limit not fixed: Volterra Unkonwn function only inside integral: first kind Also outside integral: second kind Known function f(x)=0 for all x: homogeneous f(x) 0 for some x: inhomogeneous Not all integral equations can be classified with the above. 5
- 6. Integral functions ŌĆó When differential equations are solved, integration is the final step. Sometimes there is no analytical solution to the integral. In those cases the solution is given in terms of integral functions x 2 Error function erf x exp t 2 dt 0 ŌĆó Solution of diffusion equation ŌĆó Probability theory (cumulative normal distribution) 6
- 7. Some integral functions Gamma function ŌĆó Generalization of factorial n! x t x 1e t dt 0 Incomplete gamma function x, t x 1e t dt ŌĆó Some bubble breakage models 0 /2 d Complete elliptic integral Kk ŌĆó Pendulum movement 0 1 k 2 sin 2 There are solution methods (series solution etc.) for these integrals. They are also widely tabulated 7
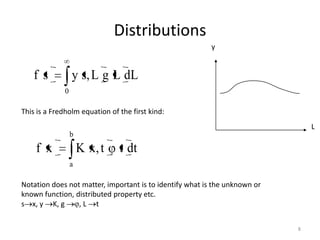
- 8. Distributions y fs y s, L g L dL 0 This is a Fredholm equation of the first kind: L b f x K x, t t dt a Notation does not matter, important is to identify what is the unknown or known function, distributed property etc. s x, y K, g ,L t 8