P vs NP
- 1. IS P=NP ? WANNA BE A MILLIONAIRE? THEN PAY ATTENTION TO THIS PRESENTATION AND YOU MIGHT JUST LEARN HOW!
- 2. PROGRESS & NEED FOR RATING STANDARD How long does it take to execute a given algorithm? In CS the answer is not given in minutes/sec. but relative to the number of elements the algorithm has to manipulate. Very difficult problems (chess) Slow ? Easy to solve problems (Addition, multiplicatio n) Fast Time to solve problems:
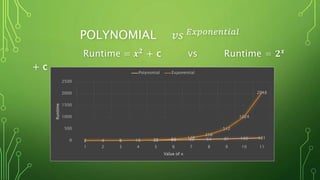
- 3. POLYNOMIAL ðĢð ðļðĨððððððĄððð Runtime = ð ð + c vs Runtime = ð ð + c 1 4 9 16 25 36 49 64 81 100 121 2 4 8 16 32 64 128 256 512 1024 2048 0 500 1000 1500 2000 2500 1 2 3 4 5 6 7 8 9 10 11 Runtime Value of x Polynomial Exponential
- 4. P class is a set of problems whose solutions running times depend polynomially on the size of the input. Thus, it is relatively easy to find these solutions using programs that are reasonably fast. NP class is a set of problems whose solution is very hard to find â perhaps requiring billions of years worth of computation â but once found, it is easily checked in polynomial time. (Salesman, Cryptography, Financial forecasting, Proteing- folding behavior, etc.) NP P
- 5. NP-complete is a set of problems X in NP for which it is possible to reduce any other NP problem Y to X in polynomial time â thus we can solve Y quickly if we can solve X quickly. These are the hardest NP problems. âĒ How to prove a problem that is NP-Complete? 1- First you need to show that it is in NP (hard to solve but can verify solution) 2- Reduce an arbitrary instance of an NP-complete problem A to an instance of your problem B in polynomial time (A<B and B<C A<C). So, if A is NP-complete, B is in NP, and A<B, B is NP - Complete. P NP- complete NP Problems
- 6. For the Traveling Salesman Problem (TSP) : -First, we have to prove that TSP belongs to NP. If we want to check a tour for credibility, we check that the tour contains each vertex once. Then we sum the total cost of the edges and finally we check if the cost is minimum. This can be completed in polynomial time thus TSP belongs to NP. -We can use the Hamilton Circuit or any other NP-complete problem (SAT) to reduce it to our TSP. Given an instance of a graph G, we create Gâē: We first make Gâē complete. We let d(ij) = 0 if edge (i, j) is in G. Otherwise, we let d(ij) = 1.
- 7. THE FUNDAMENTAL DILEMMA If the correct solution to a problem can be verified in polynomial time, can it also be found in polynomial time? So P = NP means that for every problem that has an efficiently verifiable solution, we can find that solution efficiently as well. A solution to one exercise would give the key to all NP problems. Surveys in the Scientific Community reveal that majority believe that P is not equal to NP because it is unlikely that we will be able to avoid exponential search, and that a simple trick can hardly solve all of these problems.
- 8. âĒ Solve the P vs NP dilemma and you will receive the promised prize!