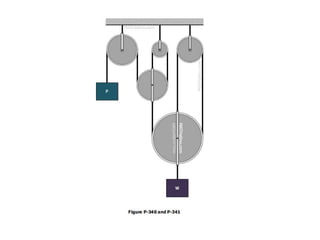
Parallel Forces
- 2. CLASSIFICATION OF PARALLEL FORCES âĒ 1. Like parallel forces. âĒ 2. Unlike parallel forces.
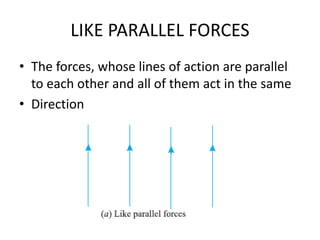
- 5. LIKE PARALLEL FORCES âĒ The forces, whose lines of action are parallel to each other and all of them act in the same âĒ Direction
- 7. UNLIKE PARALLEL FORCES The forces, whose lines of action are parallel to each other and all of them do not act in the same direction
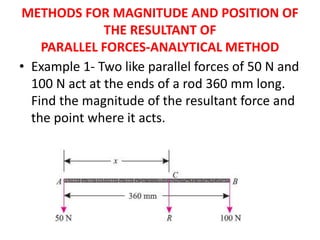
- 8. METHODS FOR MAGNITUDE AND POSITION OF THE RESULTANT OF PARALLEL FORCES-ANALYTICAL METHOD âĒ Example 1- Two like parallel forces of 50 N and 100 N act at the ends of a rod 360 mm long. Find the magnitude of the resultant force and the point where it acts.
- 9. Example 4.2. A beam 3 m long weighing 400 N is suspended in horizontal position by two vertical strings, each of which can withstand a maximum tension of 350 N only. How far a body of 200 N weight be placed on the beam, so that one of the strings may just break ?
- 10. COUPLE A pair of two equal and unlike parallel forces (i.e. forces equal in magnitude, with lines of action parallel to each other and acting in opposite directions) is known as a couple.
- 11. ARM OF A COUPLE âĒ The perpendicular distance (a), between the lines of action of the two equal and opposite parallel forces, is known as arm of the couple
- 12. MOMENT OF A COUPLE âĒ The moment of a couple is the product of the force (i.e., one of the forces of the two equal and opposite parallel forces) and the arm of the couple. Moment of a couple = P Ã a where P = Magnitude of the force, and a = Arm of the couple.
- 13. CLASSIFICATION OF COUPLES âĒ 1. Clockwise couple âĒ 2. Anticlockwise couple.
- 16. CHARACTERISTICS OF A COUPLE âĒ A couple (whether clockwise or anticlockwise) has the following characteristics : âĒ 1. The algebraic sum of the forces, constituting the couple, is zero. âĒ 2. The algebraic sum of the moments of the forces, constituting the couple, about any point âĒ is the same, and equal to the moment of the couple itself. âĒ 3. A couple cannot be balanced by a single force. But it can be balanced only by a couple of âĒ opposite sense. âĒ 4. Any no. of coplaner couples can be reduced to a single couple, whose magnitude will be âĒ equal to the algebraic sum of the moments of all the couples.
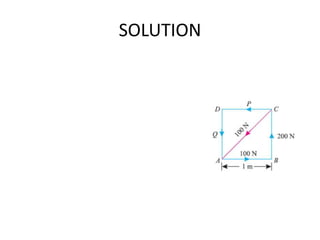
- 17. Example 1 A square ABCD has forces acting along its sides as shown in Fig. Find the values of P and Q, if the system reduces to a couple. Also find magnitude of the couple, if the side of the square is 1 m.
- 18. SOLUTION
- 19. QUESTIONS