Pattern classification
- 1. Pattern Classification using 2-D Cellular Automata
- 2. Cellular Automata - A discrete dynamical system that consists of : Each cell in of the N-dimensional grid finite number of of cells states Cells constituting Collection of rules the neighbour of determining the the cell in state of the cell in consideration the next instant
- 3. Purely local decisions Collective behavior of Behind every parallelism simple cells complex behavior lies simple logic- Cellular Automata Works well No with less modeling data constraints ŌĆó finds application in effective pattern Cellular Automata classification
- 4. Meaningful interpretation of voluminous data-DATA CLASSIFICATION Presented algorithm maps data set instance to pixel position ( 2-dimensional in this case)- PATTERN CLASSFICATION Pattern classification was proposed as an application of SweeperŌĆÖs Algorithm(SA) Combined use of SA and Majority rule as an attempt to classify iris dataset - define regions (patterns) corresponding to distinct disjoint classes of the dataset.
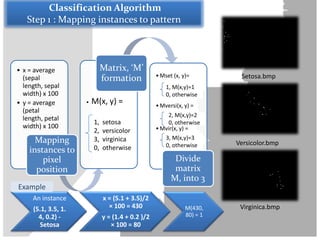
- 5. Classification Algorithm Step 1 : Mapping instances to pattern ŌĆó x = average Matrix, ŌĆśMŌĆÖ ŌĆó Mset (x, y)= Setosa.bmp (sepal formation length, sepal 1, M(x,y)=1 width) x 100 0, otherwise ŌĆó y = average ŌĆó M(x, y) = ŌĆó Mversi(x, y) = (petal 2, M(x,y)=2 length, petal 1, setosa 0, otherwise width) x 100 ŌĆó Mvir(x, y) = 2, versicolor Mapping 3, virginica 3, M(x,y)=3 0, otherwise Versicolor.bmp instances to 0, otherwise pixel Divide position matrix M, into 3 Example An instance x = (5.1 + 3.5)/2 (5.1, 3.5, 1. ├Ś 100 = 430 M(430, Virginica.bmp 4, 0.2) - y = (1.4 + 0.2 )/2 80) = 1 Setosa ├Ś 100 = 80
- 6. Classification Algorithm Step 2 : Application of SweeperŌĆÖs Algorithm SweeperŌĆÖs Algorithm Null boundary, 9 neighborhood, hybrid 2-D CA Given a destination point (x , y) Consider an axis passing through the point dividing the 2-D search region into two ( refer figure alongside) Rotate the axis through an angle of rotation,45 degrees in this case, forming 4 such set of regions In each iteration apply hybrid rules to each of these sets of regions, aimed at bringing the marked pixels a step closer to the axis As a result, after certain number of iterations, all marked pixels accumulate around the destination point.
- 7. Classification Algorithm Step 2 continued ŌĆ” Setosa.bmp Apply SweeperŌĆÖs Algorithm (application of hybrid 2-D CA rules to ŌĆśsweepŌĆÖ points near to a single destination point) to each Versicolor.bmp .bmp image files with Centroid of pixels in white as destination, for each image Virginica.bmp Combine corresponding matrices into one: MŌĆś = Mset + Mversi + Mvir Combined.bmp Write to ŌĆścombined.bmpŌĆÖ image file
- 8. Classification Algorithm Step 3 : Application of Majority Rule Majority Rule: 0 : n1 + n2 + n3 = 0 Next state of cell = 1 : n1 > n2 and n1 > n3 (applied to each pixel) 2 : n2 > n1 and n2 > n3 3 : n3 > n1 and n3 > n2 Rand(1, 2): n1 = n2 > n3 ŌĆó Moore neighborhood Rand(1, 3): n1 = n3 > n2 Verification: ŌĆó Null boundary Rand(2, 3): n2 = n3 > n1 ŌĆó Uniform Rand(1, 2, 3): n1 = n2 =n3 ŌēĀ 0 ŌĆó Map instance to pixel ŌĆó Here, ni is the numbers of neighbors of class ŌĆśIŌĆÖ. ŌĆó Check for the color assigned to the corresponding element (pixel) in matrix ŌĆó If match , increase counter ŌĆó Efficiency = (total number of Assign different colors : matches /total number of MŌĆÖi,j = 3 instances)x 100 MŌĆÖi,j = 1 setosa viriginica Conclusion: MŌĆÖi,j = 2 ŌĆó Linear and non-linear versicolor instance space classifier
- 9. ŌĆó With ŌĆśkŌĆÖ = number of instances from each class, as the training set ŌĆó 5 simulations for each value of ŌĆśkŌĆÖ ŌĆó Averaging the efficiency for all k , we obtain graph as : Efficiency : Complexity: Efficiency in the range of 2-dimensional grid in scale of 97.6┬▒ 1.5 hundred Efficiency nearly the same even 45 iterations of SweeperŌĆÖs with lesser value for k Algorithm and nearly 200 iterations of Majority rule Efficiency = 100% when classify setosa and versicolor compared cosumes nearly 21 mins. cpu to 99┬▒ 3.2 in voting rule time in a serial processor
- 10. ŌĆó An efficient linear as well as non-linear classifier (with efficiency nearly 97.6 ┬▒ 1.5 %) ŌĆó Sweeper preserves the pattern of region a class occupies ŌĆó Maps attributes to 2-dimensional grid resulting in loss of information, yet efficient. ŌĆó Generalize the algorithm for any data set ŌĆó Reduce time complexity ŌĆó Optimize sweeperŌĆÖs algorithm for minimum number of iterations ŌĆó Optimum selection of destination point to improvise the algorithm
- 11. THANK YOU