![?自?己紹介
?露露崎弘毅（つゆざき ?こうき）
?理理化学研究所 ?情報基盤センター
? ? ? ? ?バイオインフォマティクス研究開発ユニット
? ? ?（RIKEN ?ACCC ?BiT）
? ? ? ? ?特別研究員
?Single-‐??cell ?RNA-‐??Seqのデータ解析、解析?手法?ソフトウェア
開発をやっています
?連絡先
-‐?? ?@antiplastics
-‐?? ?koki.tsuyuzaki ?[at] ?gmail.com](https://image.slidesharecdn.com/pcagplvm-151113084515-lva1-app6892/85/PCA-GPLVM-2-320.jpg)
笔颁础の最终形态骋笔尝痴惭の解説
- 2. ?自?己紹介 ?露露崎弘毅（つゆざき ?こうき） ?理理化学研究所 ?情報基盤センター ? ? ? ? ?バイオインフォマティクス研究開発ユニット ? ? ?（RIKEN ?ACCC ?BiT） ? ? ? ? ?特別研究員 ?Single-‐??cell ?RNA-‐??Seqのデータ解析、解析?手法?ソフトウェア 開発をやっています ?連絡先 -‐?? ?@antiplastics -‐?? ?koki.tsuyuzaki ?[at] ?gmail.com
- 3. GPLVMってぐぐってみると... なるほど、わからん＼(^o^)／ → ?一体、何をしているのかくらいは理解したい PCA（主成分分析）のド発展版に相当する、ガウス過程を用いた GPLVMを…by ?Small ?Data ?Scien3st ?Memorandum ? PCAのお化けのような手法とでもいえばよいのでしょうか。 ? by ?京都大学医学部統計遺伝学分野 ?
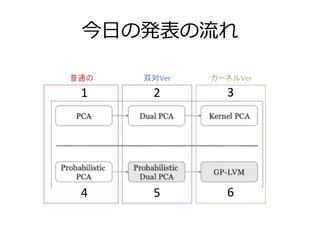
- 4. 今?日の発表の流流れ 1 2 3 4 5 6 Probabilis3c ?PCA ?with ?GPLVM この順番に話します
- 5. 今?日の発表の流流れ 1 2 3 4 5 6 決定論的な解法 確率論的な解法
- 6. 今?日の発表の流流れ 1 2 3 4 5 6 普通の カーネルVer 双対Ver
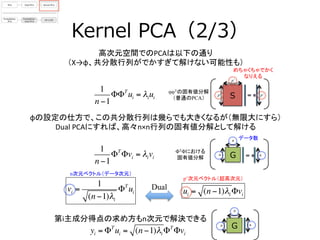
- 7. 今回のデータ p次元のデータセットXをd次元のデータセットYにする（次元圧縮） データ、サンプル（n） 次元、変数、変量 ? （p） ? データ、サンプル（n） 低次元 ? （d, ?2,3次元くらい が多い） ? X Y Xはあらかじめデータごとに平均値が 引かれているものとする
- 8. 考える上でのポイント n p ? X n p ? X XT p ? n = = XT n p ? 2種類の行列が登場 ? （形だけに注目） n n p p S G グラム行列と同じ形 ? ? p>>nの場合、サイズが小さい ? → ?計算が速い（Dual ?PCA） ? ? カーネル法と関連する ? → ?非線形性を扱える（Kernel ?PCA） ? ? こっちの方が嬉しい事が多い ? 共分散行列と同じ形 ? （通常のPCAと関係）
- 9. 補?足 ?: ?固有値分解とは ある正方行列Aにベクトルuをかけたときに、uの定数倍λに なる場合、uをAの固有ベクトル、λを固有値という =Au = λu λ, uの具体的な求め方 Aが4次元以下 → 手計算（固有方程式を解く） それ以上 →数値計算（べき乗法、ヤコビ法など） 固有値は、行列の次元だけ存在するので、行列でまとめて書くと AU =UΛ = UT AU = Λ A =UΛUT “スペクトル分解” “行列の対角化”
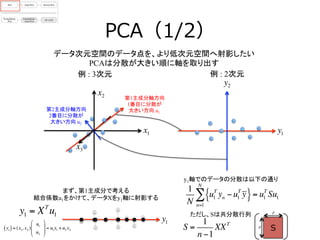
- 10. PCA（1/2） y1 データ次元空間のデータ点を、より低次元空間へ射影したい PCAは分散が大きい順に軸を取り出す 例 : 3次元 例 : 2次元 y2 x3 x1 x2 第1主成分軸方向 1番目に分散が 大きい方向 u1 第2主成分軸方向 2番目に分散が 大きい方向 u2 まず、第1主成分で考える 結合係数u1をかけて、データXをy1軸に射影する y1 = XT u1 y1 y1軸でのデータの分散は以下の通り 1 N u1 T yn ?u1 T y{ } n=1 N ∑ = u1 T Su1 ただし、Sは共分散行列 Sp p S = 1 n ?1 XXT y1( )= (x1, x2 ) u1 u2 ! " # # $ % & & = u1x1 +u2 x2
- 11. PCA（2/2） この分散を最大化させるu1を求めたいが、このままでは|u1|→∞が解 になるので、|u1|=1という拘束条件を設定する 第i主成分も、i-?‐1以前の主成分と直行するという仮定を置くことで ? 逐次的にもとめることができる（PRML下巻、演習12.1） PCA ?= ?共分散行列の固有値分解 ? 第i主成分得点 yi ?= ?XTui ? 第i主成分における分散 ?= ?ui TXui ?= ?λi f (u1,λ1) = u1 T Su1 + λ1(1?u1 T u1) ラグランジュ未定乗数法でこの最適化問題を解く ? （以下の目的関数を最大化） u1で微分する ?f (u1,λ1) ?u1 = 2Su1 ? 2λ1u1 = 0 Su1 = λ1u1 よって、u1は共分散行列Sの固有ベクトルだとわかる
- 12. 補?足 ?: ?双対とは 双対問題 f(x, y) = 2x2 + 3y2を最小にする (x, y)を求めよ ただし、x + y = 1とする g(x, y) = x + yを最大にする (x, y)を求めよ ただし、2x2+3y2 = 3/5とする x + y = 1 （拘束条件、固定） r=3/5 r=1 r=2 目的関数 g(x, y) = x + y = s 2x2 + 3y2 = 3/5 （拘束条件、固定） 目的関数 ? f(x, ?y) ?= ?2x2 ?+ ?3y2 ?= ?r s=0 s=1/2 s=1 どちらかを説いたら、両方解いたことになる関係になる場合、 ? 双対（Dual, ?Duality）という 主問題 これらは本質的に同じ問題を解いている ?
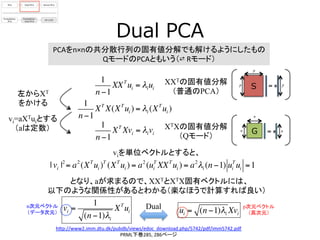
- 13. Dual ?PCA PCAをn×nの共分散行列の固有値分解でも解けるようにしたもの ? QモードのPCAともいう（? ?Rモード） ? h[p://www2.imm.dtu.dk/pubdb/views/edoc_download.php/5742/pdf/imm5742.pdf ? PRML下巻285, ?286ページ 1 n ?1 XXT ui = λiui XXTの固有値分解 （普通のPCA） 1 n ?1 XT X(XT ui ) = λi (XT ui ) 左からXT をかける XTXの固有値分解 （Qモード） 1 n ?1 XT Xvi = λivi viを単位ベクトルとすると、 vi=aXTuiとする （aは定数） | vi |2 = a2 (XT ui )T (XT ui ) = a2 (ui T XXT ui ) = a2 λi (n ?1) ui T ui =1 vi = 1 (n ?1)λi XT ui となり、aが求まるので、XXTとXTX固有ベクトルには、 以下のような関係性があるとわかる（楽なほうで計算すれば良い） ui = (n ?1)λi Xvi S =p p p G =n n n Dualn次元ベクトル （データ次元） p次元ベクトル （高次元）
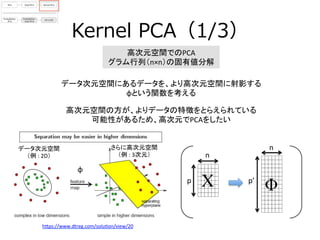
- 14. Kernel ?PCA（1/3） 高次元空間でのPCA ? グラム行列（n×n）の固有値分解 データ次元空間にあるデータを、より高次元空間に射影する ? φという関数を考える h[ps://www.dtreg.com/solu3on/view/20 ? 高次元空間の方が、よりデータの特徴をとらえられている ? 可能性があるため、高次元でPCAをしたい ? データ次元空間 ? （例 ?: ?2D） さらに高次元空間 ? （例 ?: ?3次元） φ X Φ n n p p’
- 15. Kernel ?PCA（2/3） 高次元空間でのPCAは以下の通り ? （X→φ、共分散行列がでかすぎて解けない可能性も） 1 n ?1 ΦΦT ui = λiui φφTの固有値分解 （普通のPCA） ΦTΦにおける 固有値分解 1 n ?1 ΦT Φvi = λivi S =p' p' p' G =n n n φの設定の仕方で、この共分散行列は幾らでも大きくなるが（無限大にすら） ? Dual ?PCAにすれば、高々n×n行列の固有値分解として解ける ? めちゃくちゃでかく なりえる vi = 1 (n ?1)λi ΦT ui ui = (n ?1)λi Φvi n次元ベクトル（データ次元） p’次元ベクトル（超高次元） yi = ΦT ui = (n ?1)λi ΦT Φvi 第i主成分得点の求め方もn次元で解決できる ? データ数 Gn n n Dual
- 16. Kernel ?PCA（3/3） ΦT Φそれでも ? 当然カーネル関数やパラメーターの選び方で、解析結果は大きく影響する ? 実はカーネル関数κという類似度を返す関数を使うと、 ? Φ を陽に計算せずに、内積値だけを得る事ができる（カーネルトリック） ? どのような関数でも良いというわけではなく、グラム行列が半正定値性 ? （固有値が全て0以上）を満たすものだけが、カーネル関数になれる ? を計算する上で、事前に ? を計算しないといけないのでは?と考えられるが ? Φ κ(xi, xj ) = φ(xi )T φ(xj ) n次元データ同士の 何らかの類似度（軽い） p’次元データ同士 の内積（重い） nn p' p` RBFカーネル ? カーネル関数はいっぱいある ? κ(xi, xj ) = exp(?σ xi ? xj 2 ) κ(xi, xj ) = αxi T xj +c( ) d h[p://crsouza.com/2010/03/kernel-?‐ func3ons-?‐for-?‐machine-?‐learning-?‐applica3ons/ ? 多項式カーネル ? （p’ ?× ?n行列） ? なので、カーネル関数でn×n行列（グラム行列）を計算して ? （カーネル置換）、固有値分解するだけでよい ?
- 17. p(xi | yi ) Probabilistic ?PCA PCAの確率的解法 ? xi = Wyi +ε 以下のような確率モデルを考える x1 x1 x2 x2 wy1 wで射影 ? （1D→2D） 等方性 ? ガウスノイズ p(y1) y1 潜在空間（主成分）を先に設定 wy1 x1 wy1 データのモデルへの ? 適合度（尤度）を計算 x2 p(yi ) = N(yi | 0, I) p(xi | yi ) = N(xi |Wyi,β?1 I) ← ?ガウス！ ガウス！！ ? ↓ yiの事前分布 xiの尤度 例 ?: ?２次元 ?→ ?1次元
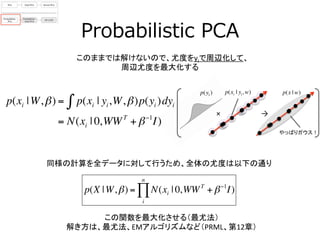
- 18. Probabilistic ?PCA このままでは解けないので、尤度をyiで周辺化して、 周辺尤度を最大化する p(xi |W,β) = p(xi | yi,W,β)p(yi )dyi∫ = N(xi | 0,WWT + β?1 I) 同様の計算を全データに対して行うため、全体の尤度は以下の通り ? p(X |W,β) = N(xi | 0,WWT + β?1 I) i n ∏ この関数を最大化させる（最尤法） ? 解き方は、最尤法、EMアルゴリズムなど（PRML、第12章） ? × → やっぱりガウス！ p(y1) p(x | w)p(xi | yi,w)
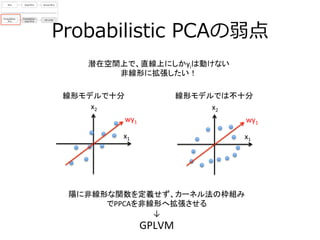
- 19. Probabilistic ?PCAの弱点 潜在空間上で、直線上にしかyiは動けない ? 非線形に拡張したい！ x1 x2 wy1 x1 x2 wy1 線形モデルで十分 線形モデルでは不十分 陽に非線形な関数を定義せず、カーネル法の枠組み でPPCAを非線形へ拡張させる ? ↓ ? GPLVM
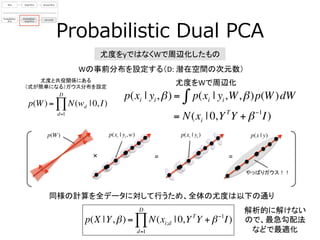
- 20. Probabilistic ?Dual ?PCA 尤度をyではなくWで周辺化したもの 尤度をWで周辺化 p(xi | yi,β) = p(xi | yi,W,β)p(W)dW∫ = N(xi | 0,YT Y + β?1 I) 同様の計算を全データに対して行うため、全体の尤度は以下の通り ? p(X |Y,β) = N(xi;d | 0,YT Y + β?1 I) d=1 D ∏ Wの事前分布を設定する（D: ?潜在空間の次元数） ? p(W) = N(wd | 0, I) d=1 D ∏ = やっぱりガウス！！ p(W) p(x | y)p(xi | yi ) 尤度と共役関係にある ? （式が簡単になる）ガウス分布を設定 =× p(xi | yi,w) 解析的に解けない ので、最急勾配法 などで最適化 ?
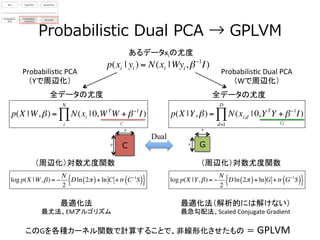
- 21. Probabilistic ?Dual ?PCA ?→ ?GPLVM あるデータxiの尤度 ? p(X |Y,β) = N(xi;d | 0,YT Y + β?1 I) d=1 D ∏p(X |W,β) = N(xi | 0,WT W + β?1 I) i N ∏ Probabilis3c ?PCA ? （Yで周辺化） Probabilis3c ?Dual ?PCA ? （Wで周辺化） p(xi | yi ) = N(xi |Wyi,β?1 I) このGを各種カーネル関数で計算することで、非線形化させたもの ＝ GPLVM Gn n Dual GC Cp p （周辺化）対数尤度関数 最適化法 ? 最尤法、EMアルゴリズム 最適化法（解析的には解けない） ? ? 最急勾配法、Scaled ?Conjugate ?Gradient （周辺化）対数尤度関数 全データの尤度 ? 全データの尤度 ? log p(X |W,β) = ? N 2 Dln 2π( )+ ln C +tr C?1 S( ){ } log p(X |Y,β) = ? N 2 Dln 2π( )+ ln G +tr G?1 S( ){ }
- 22. ちなみに 人の動作のトラッキング研究で最初に適用された経緯から、棒人間がよく登場する ? ? 歩く、飛ぶなど一連の動作は、少数の動作パターンの組み合わせでしかない ? → ?潜在空間で同じところを非線形にぐるぐる回る 計測データ ? （データ空間） 主成分得点 ? （潜在空間） h[p://www.dgp.toronto.edu/~jmwang/gpdm/2dgpdm.html ? h[p://www.cs.ubc.ca/~duoli/ ? h[ps://www.youtube.com/watch?v=YLSmvEyJo1U ? h[p://grail.cs.washington.edu/projects/styleik/ ?
- 23. GPLVMの拡張モデル ? ?Gaussian ?Process ?Dynamic ?Model（GPDM） ?: ?GPLVMの時系列データへの拡張 h[p://www.dgp.toronto.edu/~jmwang/gpdm/ ? ? ?Bayesian ?GPLVM ?: ?GPLVMのベイズ版 ? ?→ ?パラメーターの分布、データの予測分布が手に入る h[p://inverseprobability.com/vargplvm/ ?
- 24. GPLVMの拡張モデル ? ?Scaled ?Gaussian ?Process ?Latent ?Variable ?Model ?（SGPLVM） ?: ? ? ? ? ?正規化をほどこしたGPLVM ? ? ? ?h[p://www.cvlibs.net/publica3ons/Geiger2007.pdf ? ? ?Balanced ?GPDM ?（BGPDM） : 潜在空間でより滑らかにフィッティングするGPDM 比較論文 ?: ? ? Comparing ?GPLVM ?Approaches ?for ?Dimensionality ?Reduc3on ?in ?Character ?Anima3on ? ? h[p://www.cs.toronto.edu/~?eet/research/Papers/urtasunCVPR06.pdf ? ? ?Supervised ?GPDM ?（SGPLVM） : ラベル情報も利用したGPLVM（Jiang, ?X ?et ?al., ?2012） ?
- 25. バイオ分野での適?用事例例 ?Characteriza3on ?of ?transcrip3onal ?networks ?in ?blood ?stem ?and ?progenitor ?cells ?using ?high-?‐ throughput ?single-?‐cell ?gene ?expression ?analysis, ?Nature ?Cell ?Biology, ?2013 ?A ?novel ?approach ?for ?resolving ?di?erences ?in ?single-?‐cell ?gene ?expression ?pa[erns ?from ?zygote ?to ? blastocyst, ?Bioinforma2cs, ?2012 細胞の分化は8細胞期から始まるという説がある ? （Johnson ?and ?McConnell, ?2004） ? ? single-?‐cell ?qPCRで遺伝子発現を計測したところ、 ? 普通のPCAでは8細胞期でデータが分かれなかった ? ? → ?supervisedなGPLVMでデータを分けることに成功 ? ? ? ? ? ?（ラベルを与えたら、ラベルごとに分かれるのは当たり前では…?） GPLVMを血液細胞データ ? （single-?‐cell ?qPCR）に適用
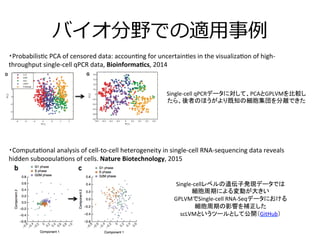
- 26. バイオ分野での適?用事例例 ?Computa3onal ?analysis ?of ?cell-?‐to-?‐cell ?heterogeneity ?in ?single-?‐cell ?RNA-?‐sequencing ?data ?reveals ? hidden ?subpopula3ons ?of ?cells, ?Nature ?Biotechnology, ?2015 ?Probabilis3c ?PCA ?of ?censored ?data: ?accoun3ng ?for ?uncertain3es ?in ?the ?visualiza3on ?of ?high-?‐ throughput ?single-?‐cell ?qPCR ?data, ?Bioinforma2cs, ?2014 Single-?‐cellレベルの遺伝子発現データでは ? 細胞周期による変動が大きい ? GPLVMでSingle-?‐cell ?RNA-?‐Seqデータにおける ? 細胞周期の影響を補正した ? scLVMというツールとして公開（GitHub） Single-?‐cell ?qPCRデータに対して、PCAとGPLVMを比較し たら、後者のほうがより既知の細胞集団を分離できた
- 27. まとめ ?? GPLVM ?= ?Probabilistic ?Kernel ?PCA ?? PCA ?→ ?共分散?行行列列（XXT）の固有値分解 ?? Dual ?PCA ?→ ?サンプル側での共分散?行行列列（XTX）の固有値分解で解いたPCA –? 嬉しいこと ?: ?pとnでサイズが?小さい?方の共分散?行行列列で計算すればよい ?? Kernel ?PCA ?→ ??高次元空間でのPCA、グラム?行行列列の固有値分解 –? 嬉しいこと ?: ??非線形への拡張 ?? Probabilistic ?PCA ?→ ?PCAの確率率率的解法 –? 嬉しいこと ?: ?予測分布が得られる（ベイズなら）、?欠損値を扱える ?? GPLVMはKernel ?PCAとProbabilistic ?PCAの両?方の性質を持つ ?? 拡張モデルが幾つも提案されている ?? バイオ分野でも多少は使われたことがある