STATISTIKA-Pengujian hipotesis
- 1. LOGO PENGUJIAN HIPOTESIS A. YOUSUF KURNIAWAN
- 2. Contents Hipotesis Statistik Pengujian Hipotesis Statistik Uji Satu-Arah dan Dua-Arah Uji Mengenai Nilaitengah yousufkurniawan@yahoo.com
- 3. HIPOTESIS STATISTIK ’üČ Hipotesis statistik adalah pernyataan atau dugaan mengenai satu atau lebih populasi (anggapan tertentu mengenai parameter populasi) ’üČ hipotesis: benar atau salah ’é« dibuktikan melalui pengujian berdasarkan pengamatan pada: ’é¦ populasi (tapi tidak rasional dilakukan) ’é¦ Contoh ’üČ hasil pengujian: ’é¦ tidak konsisten dengan hipotesis ’é« hipotesis ditolak ’é¦ konsisten dengan hipotesis ’é« hipotesis diterima ’üČ penolakan atas hipotesis: hipotesis ’é« salah ’üČ penerimaan atas hipotesis ’é« karena tidak cukup bukti untuk menolak hipotesis ’üČ hipotesis tidak dapat ditolak, tetapi tidak berimplikasi bahwa hipotesis tersebut benar
- 4. ’üČ Hipotesis: ’é¦ Hipotesis nol, H0: anggapan tertentu mengenai parameter populasi ’é« dianggap: benar jika H0 ditolak kebenarannya maka diterima H1 ’é¦ Hipotesis alternatif, H1: anggapan tandingan mengenai parameter populasi dimaksud ’üČ data (dari contoh) yang digunakan untuk: pengujian hipotesis bersifat: peubah acak ’üČ pengulangan pengujian dengan data yang berbeda dari populasi yang sama dapat menghasilkan kesimpulan pengujian yang berbeda yousufkurniawan@yahoo.com
- 5. pengujian hipotesis ’é« dipengaruhi oleh faktor ketidakpastian ’āĀ Karena itu : pemilihan atas salah satu hipotesis sebagai anggapan yang berlaku yang dilakukan melalui pengujian hipotesis + disertai: pernyataan besar peluang mengenai hipotesis yang diterima tersebut
- 6. PENGUJIAN HIPOTESIS STATISTIK 2 kantong berisi biji kedelai dalam jumlah yang ŌĆ£tidak berhinggaŌĆØ kantong pertama : daya kecambah 10% = 0.1 kantong kedua : daya kecambah 70% = 0.7 kantong yang mana? data contoh ’é« diambil 10 butir biji kedelai dari masing- masing kantong peluang mendapatkan x butir biji kedelai yang dapat mengecambah ’é« peluang binom: P (X ’ĆĮ x) ’ĆĮ b(x;10, ’ü▒ ) ’ĆĮ C(10,x)’ü▒ x (1 ’ĆŁ ’ü▒ )10’ĆŁ x X = 0, 1, ŌĆ”, 10 ╬Ė = daya kecambah www.themegallery.com
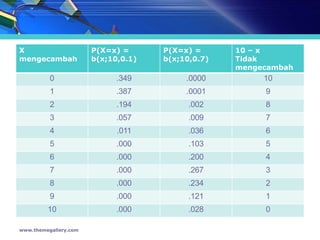
- 7. X P(X=x) = P(X=x) = 10 ŌĆō x mengecambah b(x;10,0.1) b(x;10,0.7) Tidak mengecambah 0 .349 .0000 10 1 .387 .0001 9 2 .194 .002 8 3 .057 .009 7 4 .011 .036 6 5 .000 .103 5 6 .000 .200 4 7 .000 .267 3 8 .000 .234 2 9 .000 .121 1 10 .000 .028 0 www.themegallery.com
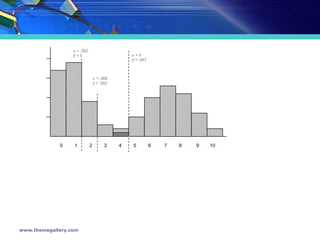
- 8. 0 1 2 3 4 5 6 7 8 9 10 ’üĪ = .262 ’üó=0 ’üĪ=0 ’üó = .047 ’üĪ = .068 ’üó = .002 0 1 2 3 4 5 6 7 8 9 10 www.themegallery.com
- 9. ’üČ Kriterium Pengujian: 10 butir kedelai ’āĀ X < 1 maka terima H0 X > 2 maka terima H1 Jika 10 butir kedelai ’āĀ X > 2 Kebenaran H0 ditolak ’āĀ selalu benar Karena : mustahil untuk mendapatkan X ’éŻ 1biji kedelai dari ’ü▒ = 0.7 yang berkecambah P(X ’éŻ 1, ’ü▒ = 0.7) = 0 H0 ditolak maka H1 diterima (’ü▒ = 0.7) P(X ’é│ 2, ’ü▒ = 0.7) = 1 H1 diterima ’é« tidak selalu benar karena: P(X ’é│ 2, ’ü▒ = 0.1) = 0.194 + 0.057 + 0.011 = 0.262 ada kemungkinan (P = 0.262) butir biji yang berkecambah berasal dari kantong ’ü▒ = 0.1 www.themegallery.com
- 10. ’üČ Kriterium Pengujian: 10 butir kedelai ’āĀ X < 2 maka terima H0 X > 3 maka tolak H0 3 4 H0 diterima H0 ditolak H1 diterima wilayah penerimaan wilayah kritik, wilayah Penolakan www.themegallery.com
- 11. - tolak H0 (’é║ terima H1), H1 benar P(X ’é│ 3 ’éĮ’ü▒ = 0.7) = 0.998 - tolak H0 (’é║ terima H1), H0 benar P(X ’é│ 3 ’éĮ’ü▒ = 0.1) = 0.068 (salah jenis I) X ’é│ 3 berasal dari ’ü▒ = 0.1 - terima H0 (’é║ tolak H1), H0 benar P(X ’éŻ 2 ’éĮ’ü▒ = 0.1) = 0.930 - terima H0 (’é║ tolak H1), H1 benar P(X ’éŻ 2 ’éĮ’ü▒ = 0.7) = 0.002 (salah jenis II) X ’éŻ 2 berasal dari ’ü▒ = 0.7 www.themegallery.com
- 12. ’üČ Kriterium Pengujian: 10 butir kedelai ’āĀ X > 5 maka tolakH0 - tolak H0 (’é║ terima H1), H1 benar P(X ’é│ 5 ’éĮ’ü▒ = 0.7) = 0.953 - tolak H0 (’é║ terima H1), H0 benar P(X ’é│ 5 ’éĮ’ü▒ = 0.1) = 0 X ’é│ 5 berasal dari ’ü▒ = 0.1 - terima H0 (’é║ tolak H1), H0 benar P(X ’éŻ 4 ’éĮ’ü▒ = 0.1) = 0.988 - terima H0 (’é║ tolak H1), H1 benar P(X ’éŻ 4 ’éĮ’ü▒ = 0.7) = 0.047 X ’éŻ 4 berasal dari ’ü▒ = 0.7 www.themegallery.com
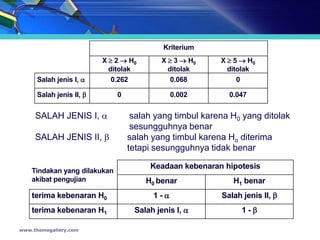
- 13. Kriterium X ’é│ 2 ’é« H0 X ’é│ 3 ’é« H0 X ’é│ 5 ’é« H0 ditolak ditolak ditolak Salah jenis I, ’üĪ 0.262 0.068 0 Salah jenis II, ’üó 0 0.002 0.047 SALAH JENIS I, ’üĪ salah yang timbul karena H0 yang ditolak sesungguhnya benar SALAH JENIS II, ’üó salah yang timbul karena Ho diterima tetapi sesungguhnya tidak benar Keadaan kebenaran hipotesis Tindakan yang dilakukan akibat pengujian H0 benar H1 benar terima kebenaran H0 1-’üĪ Salah jenis II, ’üó terima kebenaran H1 Salah jenis I, ’üĪ 1-’üó www.themegallery.com
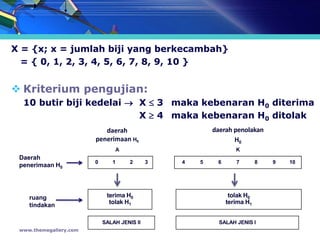
- 14. │▌’é│4 maka kebenaran H0 ditolak X = {x; x = jumlah biji yang berkecambah} = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 } ’üČ Kriterium pengujian: 10 butir biji kedelai ’é« X ’éŻ 3 maka kebenaran H0 diterima X ’é│ 4 maka kebenaran H0 ditolak daerah daerah penolakan penerimaan H0 H0 A K Daerah 0 1 2 3 4 5 6 7 8 9 10 penerimaan H0 ruang terima H0 tolak H0 tindakan tolak H1 terima H1 SALAH JENIS II SALAH JENIS I www.themegallery.com
- 15. ’üĪ = P( x Žć K ’éĮ H0 benar) 1 - ’üĪ = P( x Žć A ’éĮ H0 benar) ’üó = P( x Žć A ’éĮ H1 benar) 1 - ’üó = P( x Žć K ’éĮ H1 benar) ’é« KUASA PENGUJIAN usaha untuk mengecilkan peluang timbulnya salah satu jenis kesalahan dengan mengubah kriterium pengujian akan diikuti dengan membesarnya pembesaran nilai peluang timbulnya kesalahan jenis lain pengecilan nilai peluang kedua jenis kesalahan secara serempak hanya dapat dilakukan dengan cara memperbesar ukuran contoh Dalam aplikasi pengujian hipotesis nilai ’üĪ ditentukan: ’üĪ = 0.05 atau ’üĪ = 0.01 ’üĪ = 0.05 ’é« dikatakan: taraf-nyata pengujian = 0.05 Setiap kali kita mengambil keputusan: tolak H0 (’é║ terima H1) kita menyadari terjadinya kesalahan (salah jenis I) sebesar ’üĪ. www.themegallery.com
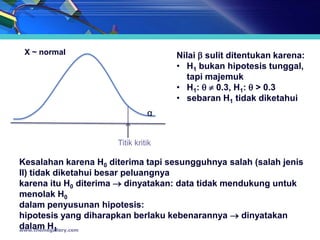
- 16. X ~ normal Nilai ’üó sulit ditentukan karena: ŌĆó H1 bukan hipotesis tunggal, tapi majemuk ŌĆó H1: ’ü▒ ’é╣ 0.3, H1: ’ü▒ > 0.3 ŌĆó sebaran H1 tidak diketahui ╬▒ Titik kritik Kesalahan karena H0 diterima tapi sesungguhnya salah (salah jenis II) tidak diketahui besar peluangnya karena itu H0 diterima ’é« dinyatakan: data tidak mendukung untuk menolak H0 dalam penyusunan hipotesis: hipotesis yang diharapkan berlaku kebenarannya ’é« dinyatakan dalam H1 www.themegallery.com
- 17. UJI SATU-ARAH, UJI DUA-ARAH Uji satu-arah: H0: ’ü▒ = ’ü▒0 vs H 1: ’ü▒ > ’ü▒ 0 H 0: ’ü▒ = ’ü▒ 0 vs H 1: ’ü▒ < ’ü▒ 0 Uji dua-arah: H0: ’ü▒ = ’ü▒0 vs H 1: ’ü▒ ’é╣ ’ü▒ 0 Pilihan atas pengujian satu-arah atau dua-arah tergantung kepada obyek yang diuji mis.: varietas padi baru ’é« uji satu-arah H1: ’ü▒ > ’ü▒0 teknik mengajar baru ’é« uji dua-arah www.themegallery.com
- 18. Latihan ’üČ Nyatakan hipotesis nol dan hipotesis alternatifnya, dan secara umum nyatakan letak wilayah kritiknya 1. Rata-rata curah hujan di Riam Kanan selama bulan Februari adalah 21.8 cm. 2. Banyaknya staf dosen suatu perguruan tinggi yang menyumbang dalam suatu acara dana sosial tidak lebih dari 20% 3. Secara rata-rata, anak sekolah berangkat dari rumah menempuh jarak tidak lebih dari 6.2 km. 4. Di tahun mendatang, sekurang-kurangnya 70% dari mobil baru termasuk dalam kategoro compact dan subcompact. 5. Dalam pemilukada mendatang, proporsi yang memilih calon petahana adalah 0.58 6. Di Obonk Steak, rata-rata steak yang dihidangkan sekurang-kurangnya 340 gram. www.themegallery.com
- 19. ’üČPENGUJIAN HIPOTESIS ’é« langkah pengujian: 1. Nyatakan hipotesis nol H0: ’ü▒ = ’ü▒0 2. Pilih hipotesis alternatif H1 yang sesuai: satu- arah atau dua-arah 3. Taraf nyata: ’üĪ 4. Statistik uji ’é« titik kritik, wilayah kritik 5. Hitung nilai statistik uji (statistik hitung) 6. Keputusan 7. Kesimpulan www.themegallery.com
- 20. H0: ’üŁ = ’üŁ0 lawan H1: ’üŁ > ’üŁ0 Populasi X ~ N(╬╝, ╬┤2) X ~ N (’üŁ x , ’ü│ 2 x ) ’üŁx ’ĆĮ ’üŁ ’ü│2 ’ü│ x’ĆĮ 2 n Transformasi normal Contoh berukuran n: x1, x2, ŌĆ” , xn X ’ĆŁ ╬╝x X’é«z’ĆĮ ’āźx Žā2x X’ĆĮ i n x ’ĆŁ ’üŁ0 Statistik uji: zhitung ’ĆĮ ’ü│x www.themegallery.com
- 21. P ( zhitung ’éŻ z’üĪ) = 1 - ’üĪ P ( zhitung > z’üĪ) = ’üĪ taraf uji Kaidah pengujian: ŌĆó zhitung ’éŻ z’üĪ ’é« terima H0 ŌĆó zhitung > z’üĪ ’é« tolak H0 Pengujian dua-arah: H0: ’üŁ = ’üŁ0 lawan H1: ’üŁ ’é╣ ’üŁ0 H1: ’üŁ ’é╣ ’üŁ0 ’é« H1: ’üŁ > ’üŁ0 atau ’üŁ < ’üŁ0 P (-z’üĪ/2 ’éŻ zhitung ’éŻ z’üĪ/2) = 1 - ’üĪ P (’éĮ zhitung ’éĮ> z’üĪ/2) = ’üĪ www.themegallery.com
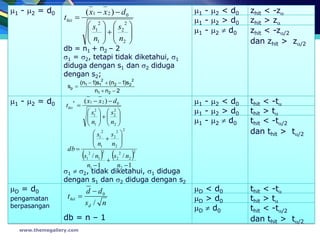
- 22. ’üŁ = ’üŁ0 x ’ĆŁ ’üŁ0 ’üŁ < ’üŁ0 zhit < -z’üĪ Z hit ’ĆĮ ’üŁ > ’üŁ0 zhit > z’üĪ ’ü│/ n ’üŁ ’é╣ ’üŁ0 zhit < -z’üĪ/2 dan ’ü│ diketahui atau n ’é│ 30 zhit > z’üĪ/2 ’üŁ = ’üŁ0 ’üŁ < ’üŁ0 thit < -t’üĪ x ’ĆŁ ’üŁ0 thit ’ĆĮ ’üŁ > ’üŁ0 thit > t’üĪ s/ n ’üŁ ’é╣ ’üŁ0 thit < -t’üĪ/2 dan db = n ŌĆō 1 thit > t’üĪ/2 ’ü│ tidak diketahui (diduga dengan s) dan n < 30 ’üŁ1 - ’üŁ2 = ( x1 ’ĆŁ x 2 ) ’ĆŁ d 0 ’üŁ1 - ’üŁ2 < d0 zhit < - z’üĪ Z hit ’ĆĮ d0 ’ā” ’ü│ 12 ’āČ ’ā” ’ü│ 2 2 ’āČ ’üŁ1 - ’üŁ2 > d0 zhit > z’üĪ ’ā¦ ’āĘ ’ā¦ ’āĘ ’üŁ1 - ’üŁ2 ’é╣ d0 ’ā¦ n ’āĘ’Ć½’ā¦ n ’āĘ zhit < - z’üĪ/2 dan ’ā© 1 ’āĖ ’ā© 2 ’āĖ zhit > z’üĪ/2 ’ü│1 dan ’ü│2 diketahui www.themegallery.com
- 23. ’üŁ1 - ’üŁ2 = d0 ( x1 ’ĆŁ x 2 ) ’ĆŁ d 0 ’üŁ1 - ’üŁ2 < d0 zhit < -z’üĪ t hit ’ĆĮ ’üŁ1 - ’üŁ2 > d0 zhit > z’üĪ ’ā” s12 ’āČ ’ā” s2 2 ’āČ ’ā¦ ’āĘ’Ć½’ā¦ ’āĘ ’üŁ1 - ’üŁ2 ’é╣ d0 zhit < -z’üĪ/2 ’ā¦n ’āĘ ’ā¦n ’āĘ ’ā© 1’āĖ ’ā© 2 ’āĖ dan zhit > z’üĪ/2 db = n1 + n2 ŌĆō 2 ’ü│1 = ’ü│2, tetapi tidak diketahui, ’ü│1 diduga dengan s1 dan ’ü│2 diduga dengan s2; 2 2 (n ’ĆŁ 1)s1 ’Ć½ (n2 ’ĆŁ 1)s2 sp ’ĆĮ 1 n1 ’Ć½ n2 ’ĆŁ 2 ’üŁ1 - ’üŁ2 = d0 t hit ’ĆĮ * ( x1 ’ĆŁ x 2 ) ’ĆŁ d 0 ’üŁ1 - ’üŁ2 < d0 thit < -t’üĪ ’ā” s12 ’āČ ’ā” s2 ’āČ 2 ’üŁ1 - ’üŁ2 > d0 thit > t’üĪ ’ā¦ ’āĘ’Ć½’ā¦ ’āĘ ’ā¦n ’āĘ ’ā¦n ’āĘ ’ā© 1’āĖ ’ā© 2’āĖ ’üŁ1 - ’üŁ2 ’é╣ d0 thit < -t’üĪ/2 ’ā” s12 s2 2 ’āČ 2 dan thit > t’üĪ/2 ’ā¦ ’Ć½ ’āĘ ’ā¦n n2 ’āĘ db ’ĆĮ ’ā© 1 ’āĖ ’Ć©s 1 2 / n1’Ć® ’Ć© 2 2 s / n2 ’Ć½ 2 ’Ć® 2 n1 ’ĆŁ 1 n2 ’ĆŁ 1 ’ü│1 ’é╣ ’ü│2, tidak diketahui, ’ü│1 diduga dengan s1 dan ’ü│2 diduga dengan s2 ’üŁD = d0 d ’ĆŁ d0 ’üŁD < d0 thit < -t’üĪ pengamatan t hit ’ĆĮ ’üŁD > d0 thit > t’üĪ berpasangan sd / n ’üŁD ’é╣ d0 thit < -t’üĪ/2 db = n ŌĆō 1 dan thit > t’üĪ/2 www.themegallery.com
- 24. Teladan 1. Sebuah perusahaan alat olah raga mengembangkan jenis batang pancing, yang dikatakan mempunyai kekuatan dengan nilai tengah 8 kg dan simpangan baku 0,5 kg. Ujilah hipotesis bahwa ’üŁ = 8 kg lawan alternatifnya ’üŁ ’é╣ 8 kg bila satu contoh acak 50 batang pancing itu setelah dites memberikan kekuatan nilai tengah 7,8 kg. Gunakan taraf nyata 0,01. Jawab. 1. H0: ’üŁ = 8 kg 2. H1: ’üŁ ’é╣ 8 kg 3. ’üĪ = 0,01 4. ’üĪ/2 = 0,005 ’é« wilayah kritik: z < -2,575 dan z > 2,575 x ’ĆŁ ’üŁ0 7,8 ’ĆŁ 8 5. x = 7,8 kg dan n = 50 ’é« zhit = = 0,5 / 50 = -2,83 ’ü│/ n 6. Keputusan: tolak H0 7. Kesimpulan: kekuatan batang pancing tidak sama dengan 8 kg, tetapi kurang dari 8 kg. www.themegallery.com
- 25. Teladan 2. Suatu contoh acak 100 catatan kematian di Amerika Serikat selama tahun lalu menunjukkan rata-rata umur seseorang meninggal 71,8 tahun dengan simpangan baku 8,9 tahun. Apakah ini menunjukkan bahwa harapan umur sekarang ini lebih dari 70 tahun? Gunakan taraf nyata 0,05. Jawab. 1. H0: ’üŁ = 70 tahun 2. H1: ’üŁ > 70 tahun 3. ’üĪ = 0,05 4. ’üĪ = 0,05 ’é« wilayah kritik: z > 1,645 x ’ĆŁ ’üŁ0 71,8 ’ĆŁ 70 5. x = 71,8 tahun, Žā Ōēł s = 8,9 tahun dan n = 100 ’é« zhit = = = 2,02 ’ü│/ n 8,9 / 100 6. Keputusan: tolak H0 7. Kesimpulan: harapan umur sekarang ini memang lebih besar dari 70 tahun www.themegallery.com
- 26. QUIZ Suatu contoh acak 8 batang rokok merk Kadal Mild memiliki kadar nikotin rata-rata 4.2 mg dengan simpangan baku 1.4 mg. Apakah hasil analisis ini sejalan dengan pernyataan perusahaan tersebut bahwa kadar nikotin rata-rata pada rokok yang dihasilkan tidak melebihi 3.5 mg? Gunakan taraf nyata 0.01 (titik kritik Uji satu-arah 2.998, uji dua-arah 3.499) dan asumsikan bahwa sebaran kadar nikotin tersebut adalah normal. www.themegallery.com
- 27. Uji Nilai Tengah - Aplikasi Komputer Ujilah hipotesis bahwa isi kaleng rata-rata suatu jenis minyak pelumas adalah 10 liter bila isi suatu contoh acak 10 kaleng adalah 10.2; 9.7; 10.1; 10.3; 10.1; 9.8; 9.9; 10.4; 10.3; dan 9.8 liter. Gunakan taraf nyata 0.01 dan asumsikan bahwa isi tersebut menyebar normal. Isi Kaleng Rata St Dev 10.2 9.7 10.1 10.3 10.1 9.8 9.9 10.4 10.3 9.8 10.06 0.245 x ’ĆŁ ’üŁ0 10,06 ’ĆŁ 10 t hit ’ĆĮ ’ĆĮ ’ĆĮ 0,772 Keputusan : Terima Ho s/ n 0,2458 Kesimpulan : Isi kaleng rata-rata = 10 10 liter t0.01 = 2.821 Bandingkan dengan menggunakan SPSS
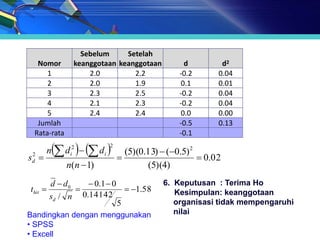
- 28. Untuk mengetahui apakah keanggotaan organisasi dalam mahasiswa mempunyai akibat baik atau buruk pada nilai seseorang, nilai mutu rata- rata berikut ini dikumpulkan. Sebelum Setelah Dengan mengasumsikan bahwa populasinya keanggotaan keanggotaan normal, ujilah pada taraf nyata 0.025 apakah 2.0 2.2 keanggotaan dalam organisasi mahasiswa 2.0 1.9 berakibat buruk pada nilai yang dicapai seseorang 2.3 2.5 2.1 2.3 2.4 2.4 1. H0: ╬╝1 = ╬╝2 atau ╬╝D = ╬╝1 ŌĆō ╬╝2 = 0 2. H1 : ╬╝1 < ╬╝2 atau ╬╝D = ╬╝1 ŌĆō ╬╝2 < 0 3. ╬▒ = 0.025 4. Wilayah kritik: t < -2.776 5. Perhitungan: www.themegallery.com
- 29. Sebelum Setelah Nomor keanggotaan keanggotaan d d2 1 2.0 2.2 -0.2 0.04 2 2.0 1.9 0.1 0.01 3 2.3 2.5 -0.2 0.04 4 2.1 2.3 -0.2 0.04 5 2.4 2.4 0.0 0.00 Jumlah -0.5 0.13 Rata-rata -0.1 s ’ĆĮ 2 ’Ć© i 2 ’Ć® n ’āź d ’ĆŁ ’Ć©’āź d i ’Ć® 2 ’ĆĮ (5)(0.13) ’ĆŁ (’ĆŁ0.5) 2 ’ĆĮ 0.02 n(n ’ĆŁ 1) d (5)(4) d ’ĆŁ d0 ’ĆŁ 0.1 ’ĆŁ 0 6. Keputusan : Terima Ho thit ’ĆĮ ’ĆĮ ’ĆĮ ’ĆŁ1.58 Kesimpulan: keanggotaan sd / n 0.14142 5 organisasi tidak mempengaruhi Bandingkan dengan menggunakan nilai ŌĆó SPSS ŌĆó Excell
- 30. TUGAS - II 1. Sebuah pabrik mobil ingin memutuskan apakah akan menggunakan ban merk A atau merk B. Untuk membantu pencapaian keputusan tersebut, sebuah percobaan dilakukan dengan menggunakan 12 ban untuk masing-masing merk tersebut. Ban-ban tersebut dipasang dan digunakan sampai aus sehingga harus diganti. Hasilnya adalah: Merk A : rata-rata X1 = 37.900 km, s1 = 5.100 km Merk B : rata-rata X2 = 39.800 km, s1 = 5.900 km Ujilah hipotesis pada taraf nyata 0.05 bahwa ada perbedaan antara kedua merk ban tersebut. Asumsikan bahwa kedua populasi menyebar menghampiri normal www.themegallery.com
- 31. TUGAS - II 2. Data di bawah ini menunjukkan masa putar film yang diproduksi dua perusahaan film yang berbeda Perusahaan Masa Putar (menit) Cineplex 102 86 98 109 92 Blitz 81 165 97 134 92 87 114 Ujilah hipotesis bahwa masa putar rata-rata film yang diproduksi perusahaan Blitz melebihi masa putar rata-rata film yang diproduksi perusahaan Cineplex sebesar 10 menit lawan hipotesis alternatifnya bahwa selisih masa putar tersebut lebih dari 10 menit. Gunakan taraf nyata 0.1 dan asumsikan bahwa kedua sebaran tersebut menghampiri normal Kerjakan perhitungannya secara manual www.themegallery.com
- 32. TUGAS - II 3. Suatu Diet baru dapat mengurangi bobot badan seseorang. Berikut ini dicantumkan bobot badan 7 wanita sebelum dan sesudah mengikuti diet selama periode 2 minggu Wanita 1 2 3 4 5 6 7 Before 58.5 60.3 61.7 69.0 64.0 62.6 56.7 After 60.0 54.9 58.1 62.1 58.5 59.9 54.4 Ujilah pada taraf nyata 0.01 hipotesis bahwa ┬Ą1 = ┬Ą2 lawan hipotesis alternatifnya ┬Ą1 < ┬Ą2. Kerjakan perhitungannya dengan SPSS dan lampirkan hasil print-out nya www.themegallery.com
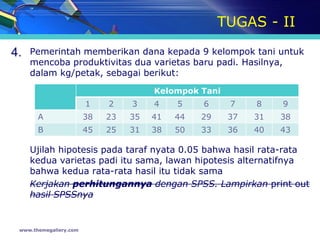
- 33. TUGAS - II 4. Pemerintah memberikan dana kepada 9 kelompok tani untuk mencoba produktivitas dua varietas baru padi. Hasilnya, dalam kg/petak, sebagai berikut: Kelompok Tani 1 2 3 4 5 6 7 8 9 A 38 23 35 41 44 29 37 31 38 B 45 25 31 38 50 33 36 40 43 Ujilah hipotesis pada taraf nyata 0.05 bahwa hasil rata-rata kedua varietas padi itu sama, lawan hipotesis alternatifnya bahwa kedua rata-rata hasil itu tidak sama Kerjakan perhitungannya dengan SPSS. Lampirkan print out hasil SPSSnya www.themegallery.com
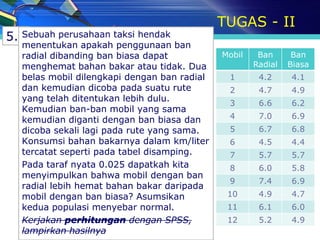
- 34. TUGAS - II 5. Sebuah perusahaan taksi hendak menentukan apakah penggunaan ban radial dibanding ban biasa dapat Mobil Ban Ban menghemat bahan bakar atau tidak. Dua Radial Biasa belas mobil dilengkapi dengan ban radial 1 4.2 4.1 dan kemudian dicoba pada suatu rute 2 4.7 4.9 yang telah ditentukan lebih dulu. 3 6.6 6.2 Kemudian ban-ban mobil yang sama kemudian diganti dengan ban biasa dan 4 7.0 6.9 dicoba sekali lagi pada rute yang sama. 5 6.7 6.8 Konsumsi bahan bakarnya dalam km/liter 6 4.5 4.4 tercatat seperti pada tabel disamping. 7 5.7 5.7 Pada taraf nyata 0.025 dapatkah kita 8 6.0 5.8 menyimpulkan bahwa mobil dengan ban 9 7.4 6.9 radial lebih hemat bahan bakar daripada mobil dengan ban biasa? Asumsikan 10 4.9 4.7 kedua populasi menyebar normal. 11 6.1 6.0 Kerjakan perhitungan dengan SPSS, 12 5.2 4.9 lampirkan hasilnya
- 35. LOGO yousufkurniawan@yahoo.com