Pitagorin poucak
Download as PPT, PDF
1 like2,123 views
Ova prezentacija je tu za one koji zele nauciti nesto o pitagorinom poucku i provjezbati par zadataka
Pitagorin poucak
- 2. 2/20 Pitagorin pouak Ako etiri povr邸inom jednaka trokuta iz lijevog kvadrata drugaije slo転imo, dobit emo desni lik.
- 3. 3/20 Na prethodnom prikazu vidimo da je zbroj povr邸ina kvadrata nad katetama po povr邸ini jednak kvadratu nad hipotenuzom Ovu povezanost izmeu duljina kateta i duljine hipotenuze u pravokutnom trokutu nazivamo Pitagorinim poukom
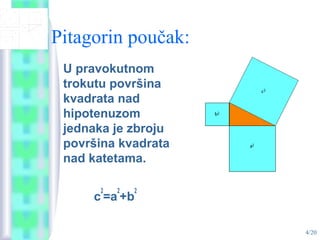
- 4. 4/20 Pitagorin pouak: U pravokutnom trokutu povr邸ina kvadrata nad hipotenuzom jednaka je zbroju povr邸ina kvadrata nad katetama. c 2 =a 2 +b 2
- 5. 5/20 Napomena: Pravokutni trokut kojemu su duljine stranica prirodni brojevi nazivamo Pitagorinim trokutom.
- 6. 6/20 Primjer 1. U pravokutnom trokutu ABC mo転emo izraunati duljinu hipotenuze ako su poznate duljine kateta: a = 6.5 cm i b = 3.8 cm. cmc cmc bac bac 5.7 8.35.6 22 22 222 = += += += Pomo Kako napisati Formulu
- 7. 7/20 Primjer 2. Ako je poznata duljina jedne katete a = 4.3 cm i duljina hipotenuze c = 12.1 cm primjenom Pitagorina pouka mo転emo izraunati duljinu druge katete. cmb cmb acb acb 3.11 3.41.12 22 22 222 = = = =
- 8. 8/20 Zadaci za vje転bu: Izraunavanje hipotenuze Izraunavanje katete a Izraunavanje katete b Primjena Pitagorina pouka Kraj
- 9. 9/20 Izraunavanje hipotenuze U trokutu ABC izraunaj kolika je duljina hipotenuze c ako je a = 6.2 cm i b = 8.4 cm. a) 38.44 cm b) 2.89 cm c) 10.44 cm d) 109 cm
- 10. 10/20 Izraunavanje katete a U trokutu ABC izraunaj kolika je duljina katete a ako je b = 5.3 cm i c = 8.9 cm. a) 7.14 cm b) 28.09 cm c) 51.12 cm
- 11. 11/20 Izraunavanje katete b U trokutu ABC izraunaj kolika je duljina katete b ako je a = 4.2 cm i c = 8.2 cm. a) 17.64 cm b) 7.04 cm c) 49.6 cm
- 12. 12/20 Primjena Pitagorina pouka Koliku e visinu dosei preklopljene ljestve duljine 2.5 m ako je za stabilnost ljestava na tlu potreban razmak 1.2 m? a) 2.42 m b) 1.44 m c) 1.58 m
- 13. 13/20 Bravo! Tono si rije邸io postavljeni zadatak.
- 15. 15/20 Zadatak 1. Postupak cmc cmc bac bac 44.10 4.82.6 22 22 222 = += += +=
- 16. 16/20 Zadatak 2. Postupak cma cma bca bca 14.7 3.59.8 22 22 222 = = = =
- 17. 17/20 Zadatak 3. Postupak cmb cmb acb acb 04.7 2.42.8 22 22 222 = = = =
- 18. 18/20 Zadatak 4. Postupak mb mb acb acb 42.2 6.05.2 22 22 222 = = = =
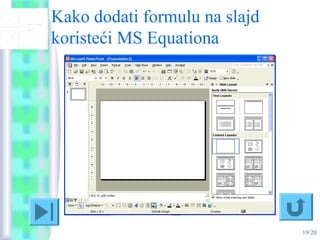
- 19. 19/20 Kako dodati formulu na slajd koristei MS Equationa
- 20. 20/20 Kraj