Poisson distribution
- 2. Probability Model: Binomial Distribution. Poison Distribution Normal Distribution.
- 4. Defination:
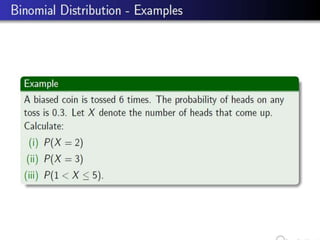
- 5. Examples:
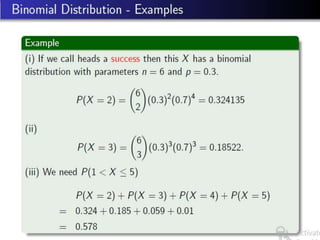
- 6. Examples::
- 7. Examples:::
- 21. Probability Model: Binomial Distribution. Poison Distribution Normal Distribution.
- 23. Historical Note: Discovered by Mathematician Simeon Poisson in France in 1781. The modelling distribution that takes his name was originally derived as an approximation to the binomial distribution.
- 24. Defination: Is an eg of a probability model which is usually defined by the mean no. of occurrences in a time interval and simply denoted by 了.
- 25. Uses: Occurrences are independent. Occurrences are random. The probability of an occurrence is constant over time.
- 26. Sum of two Poisson distributions: If two independent random variables both have Poisson distributions with parameters 了 and 亮, then their sum also has a Poisson distribution and its parameter is 了 + 亮 .
- 27. The Poisson distribution may be used to model a binomial distribution, B(n, p) provided that n is large. p is small. np is not too large.
- 28. F o r m u l a: The probability that there are r occurrences in a given interval is given by Where, = Mean no. of occurrences in a time interval r =No. of trials.
- 29. The Poisson distribution is defined by a parameter, 了.
- 30. Mean and Variance of Poisson Distribution If 亮 is the average number of successes occurring in a given time interval or region in the Poisson distribution, then the mean and the variance of the Poisson distribution are both equal to 亮. i.e. E(X) = 亮 & V(X) = 2 = 亮
- 31. Examples: 1. Number of telephone calls in a week. 2. Number of people arriving at a checkout in a day. 3. Number of industrial accidents per month in a manufacturing plant.
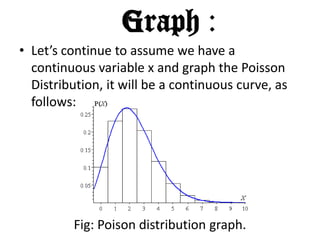
- 32. Graph : Lets continue to assume we have a continuous variable x and graph the Poisson Distribution, it will be a continuous curve, as follows: Fig: Poison distribution graph.
- 33. Example: Twenty sheets of aluminum alloy were examined for surface flaws. The frequency of the number of sheets with a given number of flaws per sheet was as follows: What is the probability of finding a sheet chosen at random which contains 3 or more surface flaws?
- 34. Generally, X = number of events, distributed independently in time, occurring in a fixed time interval. X is a Poisson variable with pdf: where is the average.
- 35. Application: The Poisson distribution arises in two ways:
- 36. 1. As an approximation to the binomial when p is small and n is large: Example: In auditing when examining accounts for errors; n, the sample size, is usually large. p, the error rate, is usually small.
- 37. 2. Events distributed independently of one another in time: X = the number of events occurring in a fixed time interval has a Poisson distribution. Example: X = the number of telephone calls in an hour.
- 39. Probability Model: Binomial Distribution. Poison Distribution Normal Distribution.
- 53. The End
- 54. Thank You.