Polinomis 4t ESO
- 1. Unitat 41: Polinomis 1. Recordatori conceptes 2. Operacions bsiques 3. Regla de Ruffini 4. Factoritzaci坦 de polinomis 5. Simplificaci坦 de fraccions algebraiques 6. Binomi de Newton
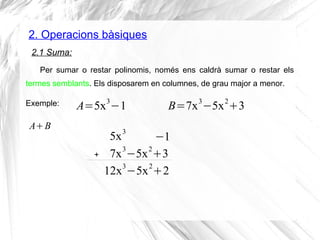
- 2. 1. Recordatori conceptes a) Nomenclatura Polinomi de grau 4 11x3 y7xy2 +5x13 Terme b) Grau d'un polinomi: el m辿s alt dels termes que el formen. p56 E1, 3 Un polinomi 辿s la suma indicada de diversos monomis no semblants. ("poli"="molts", "mono"="un de sol") Terme Terme Terme Grau 4 Grau 3 Grau 1 Grau 0 c) Oposat d'un polinomi: s'obt辿 canviant els signes de cada terme d) Valor num竪ric d'un polinomi: valor que pren el polinomi quan en coneixem les variables
- 3. 2. Operacions bsiques 2.1 Suma: A=5x3 1 Per sumar o restar polinomis, nom辿s ens caldr sumar o restar els termes semblants. Els disposarem en columnes, de grau major a menor. Exemple: B=7x3 5x2 +3 A+B 5x 3 7x 3 5x 2 +3+ 1 12x 3 5x 2 +2
- 4. 2.2 Resta: A=5x3 1 Restar 辿s el mateix que sumar l'oposat. Aix鱈, procedirem de la mateixa manera per嘆 sumant l'oposat del polinomi que actua de subtrahend. Exemple: B=7x3 5x2 +3 AB=A+(B) 5x3 7x3 +5x2 3+ 1 2x 3 +5x 2 4
- 5. P(x)=3x2 2x+7 E2, 1, 2, 26, 27, 28 Exemple: Q(x)=3x5 P(x)揃Q(x) x 15x 2 +10x35 3x2 2x+7 3x5 9x3 6x2 +21x 9x3 21x2 +31x35 2.3 Multiplicaci坦:
- 6. p57 E3, 5, 34 P(x) Q(x) C(x) R(x) 4x3 +2x2 4x+3 2.4 Divisi坦 de polinomis Dividend Divisor Quocient Residu -Dividir 1r terme de P(x) entre el 1r terme de Q(x) per obtenir 1r de C(x) -Multiplicar resultat per Q(x) i restar-lo a P(x) per obtenir nou dividend. -Repetir operaci坦 fins que R(x) sigui de menys grau que Q(x). 2x2 x+1 2x4x3 +2x2 2x 4x2 6x+3 +2 4x2 +2x2 4x+1
- 7. 3. Regla de Ruffini La regla de Ruffini ens permet fer divisions rpidament quan el divisor 辿s un binomi del tipus x a, essent a un nombre enter. Paolo Ruffini (1765-1822) Metge, fil嘆sof i matemtic. Primer fer (x3 +1):(x-2) com fins ara. 1 0 0 1 2 1 2 2 4 4 8 9 El quocient 辿s x2 + 2x + 4 i el residu 辿s 9. 8, 9, 10, 37, 38, 40
- 8. 4. Factoritzaci坦 de polinomis Un nombre a 辿s arrel d'un polinomi P(x) si es compleix que P(x) 辿s divisible per x a. La divisi坦 ha de tenir un residu igual a 0. Recordatori factoritzaci坦 de nombres naturals. 4.1 Arrels d'un polinomi -Quines s坦n les arrels del polinomi P(x) = x2 + 2x 3 ? Propietats: -L'arrel (nombre a) ha de ser divisor del terme independent. -El nombre d'arrels mai ser superior al grau del polinomi. p59 E5 1r: Poden ser: Div (-3) = {+1,-1,3,-3}
- 9. 1 2 -3 +1 1 1 3 3 0 -Quines s坦n les arrels del polinomi P(x) = x2 + 2x 3 ? 1r: Poden ser: Div (-3) = {+1,-1,3,-3} 2n: Anar comprovant per Ruffini 1 2 -3 - 3 1 -3 -1 3 0 3r: Les arrels s坦n 1 i -3 p59 11, 12, 49, 50, 51
- 10. 1 2 -3 +1 1 1 3 3 0 -Quines s坦n les arrels del polinomi P(x) = x2 + 2x 3 ? 1r: Poden ser: Div (-3) = {+1,-1,3,-3} 2n: Anar comprovant per Ruffini 1 2 -3 - 3 1 -3 -1 3 0 3r: Les arrels s坦n 1 i -3 p59 11, 12, 49, 50, 51
- 11. Factoritzar un polinomi consisteix en anar trobant binomis divisors de tipus x a fins a arribar a un polinomi irreductible, essent a una arrel del polinomi. 4.2 La factoritzaci坦 d'un polinomi -Exemple: factoritzar el polinomi P(x) = x4 2x3 + 3x2 + 2x 4 ? 1r: Les arrels poden ser: Div (-4) = {+1,-1, 2, -2, 4,-4} 2n: Anar encadenant Ruffini's, comen巽ant de nou cada vegada: 1 -2 3 2 -4 1 1 1 -1 -1 2 2 4 4 0 -1 -1 2 -4 1 -2 4 0
- 12. -Exemple: factoritzar el polinomi P(x) = x4 2x3 + 3x2 + 2x 4 ? p61 fact. els del 17, E9b, 20 extret, 63, 64 1r: Les arrels poden ser: Div (-3) = {+1,-1, 2, -2, 4,-4} 2n: Anar encadenant Ruffini's, comen巽ant de nou cada vegada: 1 -2 3 2 -4 1 1 1 -1 -1 2 2 4 4 0 -1 -1 2 -4 1 -2 4 0 3r: Interpretar el resultat: P(x) = x4 2x3 + 3x2 + 2x 4 = (x 1)揃(x + 1)揃(x2 2x + 4)
- 13. 5. Simplificaci坦 de fraccions algebraiques -Una fracci坦 algebraica 辿s aquella formada pel numerador i denominador en forma de polinomis. -Per simplificar-les factoritzarem els dos polinomis i n'eliminarem els factors comuns. Exemple: p63 23,24,69,72,73 x2 +x x 2 +2x+1 x2 +x=x揃(x+1) El numerador: (no puc fer Ruffini, extrec factor com炭) Exemple: x2 +2x+1=(x+1)揃(x+1) El denominador: (faig Ruffini) 1 2 1 - 1 1 -1 1 -1 0 = x揃(x+1) (x+1)揃(x+1) = x x+1
- 14. 6. El binomi de Newton p60 E7, 14, 16, 55, 57 (x+ y)0 = (x+ y)1 = (x+ y)2 = (x+ y)3 = (x+ y)4 = 1 x+ y (x+ y)(x+ y)= x4 +4x3 y+6x2 y2 +4xy3 +y4 x2 +xy+ yx+ y2 = x2 +2xy+y2 (x+ y)(x2 +2xy+y2 )=(x3 +2x2 y+xy2 +yx2 +2xy2 + y3 ) =x3 +3x2 y+3xy2 +y3 1 11 2 33 1 1 1 1 1 51 6 1010 1 15 4 4 Triangle de Tartaglia: (a+b)n =A揃an +B揃an1 b+C 揃 an2 b2 +...+X 揃bn