powerpoints probability.pptx
Download as pptx, pdf0 likes106 views
This document provides an overview of a lesson on sample spaces, subsets, and basic probability. It defines a sample space as the set of all possible outcomes of an event. It gives examples of sample spaces for tossing a coin, rolling a die, and drawing from a bag of marbles. It also discusses intersections and unions of sets, using Venn diagrams to visualize set relationships. The document concludes with examples of finding the probability of mutually exclusive and inclusive events using formulas and two-way tables.
powerpoints probability.pptx
- 1. Lesson 1: Sample Spaces, Subsets, and Basic Probability Math 2 Unit 9 - Probability
- 2. Lesson 1: Sample Spaces, Subsets, and Basic Probability Math 2 Unit 9 - Probability
- 3. Sample Space is the set of ALL possible outcomes of an event. List the sample space, S, for each of the following: a. Tossing a coin. S = {H, T} b. Rolling a standard six-sided die. S = {1, 2, 3 ,4, 5, 6} c. Drawing a marble from a bag that contains two red, three blue and one white marble. S = {red, red, blue, blue, blue, white}
- 4. Sample Space is the set of ALL possible outcomes of an event. List the sample space, S, for each of the following: a. Tossing a coin. S = {H, T} b. Rolling a standard six-sided die. S = {1, 2, 3 ,4, 5, 6} c. Drawing a marble from a bag that contains two red, three blue and one white marble. S = {red, red, blue, blue, blue, white}
- 5. Sample Space is the set of ALL possible outcomes of an event. List the sample space, S, for each of the following: a. Tossing a coin. S = {H, T} b. Rolling a standard six-sided die. S = {1, 2, 3 ,4, 5, 6} c. Drawing a marble from a bag that contains two red, three blue and one white marble. S = {red, red, blue, blue, blue, white}
- 6. Intersection and Union of Sets The intersection of two sets (A B) is the set of all the elements in both set A AND set B. The union of two sets (A B) is the set of all the elements in set A OR set B. Example: Given the following sets A and B, find A B and A B. A = {1,3,5,7,9,11,13,15} B = {0,3,6,9,12,15} A B = {3, 9, 15} A B = {0, 1 , 3, 5, 6, 7, 9, 11, 12, 13, 15}
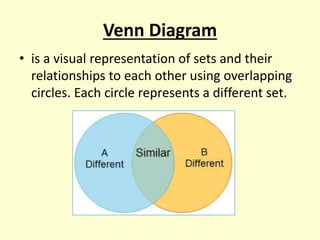
- 7. Venn Diagram is a visual representation of sets and their relationships to each other using overlapping circles. Each circle represents a different set.
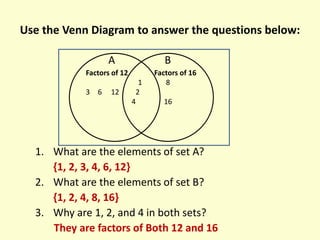
- 8. Use the Venn Diagram to answer the questions below: A B 1. What are the elements of set A? {1, 2, 3, 4, 6, 12} 2. What are the elements of set B? {1, 2, 4, 8, 16} 3. Why are 1, 2, and 4 in both sets? They are factors of Both 12 and 16 Factors of 12 1 3 6 12 2 4 Factors of 16 8 16
- 9. A B 4. What is A B? {1, 2, 4} 5. What is A B? {1, 2, 3, 4, 6 ,8, 12, 16} Factors of 12 1 3 6 12 2 4 Factors of 16 8 16
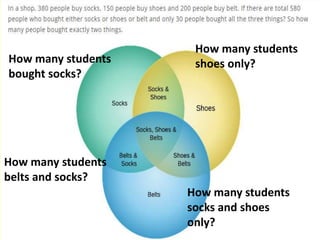
- 10. In a class of 60 students, 21 sign up for chorus, 29 sign up for band, and 5 take both. 15 students in the class are not enrolled in either band or chorus. 6. Put this information into a Venn Diagram. If the sample space, S, is the set of all students in the class, let students in chorus be set A and students in band be set B. 7. How many students are in A B? 8. How many students are in A B?
- 11. How many students bought socks? How many students belts and socks? How many students shoes only? How many students socks and shoes only?
- 13. Lesson 3: Mutually Exclusive and Inclusive Events Math 2 Unit 9 - Probability
- 14. Mutually Exclusive Events Suppose you are rolling a six-sided die. What is the probability that you roll an odd number or you roll a 2? Can these both occur at the same time? Why or why not? Mutually Exclusive Events (or Disjoint Events): Two or more events that cannot occur at the same time. The probability of two mutually exclusive events occurring at the same time , P(A and B), is 0! Video on Mutually Exclusive Events
- 15. Probability of Mutually Exclusive Events To find the probability of one of two mutually exclusive events occurring, use the following formula: P(A or B) = P(A) + P(B)
- 16. Examples 1. If you randomly chose one of the integers 1 10, what is the probability of choosing either an odd number or an even number? Are these mutually exclusive events? Why or why not? Complete the following statement: P(odd or even) = P(_____) + P(_____) P(odd or even) = P(odd) + P(even) Now fill in with numbers: P(odd or even) = _______ + ________ P(odd or even) = 遜 + 遜 = 1 Does this answer make sense?
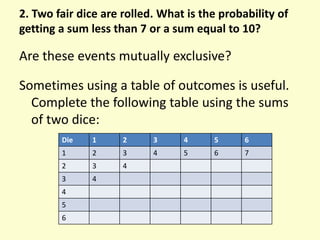
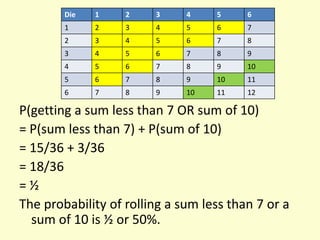
- 17. 2. Two fair dice are rolled. What is the probability of getting a sum less than 7 or a sum equal to 10? Are these events mutually exclusive? Sometimes using a table of outcomes is useful. Complete the following table using the sums of two dice: Die 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 3 4 4 5 6
- 18. P(getting a sum less than 7 OR sum of 10) = P(sum less than 7) + P(sum of 10) = 15/36 + 3/36 = 18/36 = 遜 The probability of rolling a sum less than 7 or a sum of 10 is 遜 or 50%. Die 1 2 3 4 5 6 1 2 3 4 5 6 7 2 3 4 5 6 7 8 3 4 5 6 7 8 9 4 5 6 7 8 9 10 5 6 7 8 9 10 11 6 7 8 9 10 11 12
- 19. Mutually Inclusive Events Suppose you are rolling a six-sided die. What is the probability that you roll an odd number or a number less than 4? Can these both occur at the same time? If so, when? Mutually Inclusive Events: Two events that can occur at the same time. Video on Mutually Inclusive Events
- 20. Probability of the Union of Two Events: The Addition Rule We just saw that the formula for finding the probability of two mutually inclusive events can also be used for mutually exclusive events, so lets think of it as the formula for finding the probability of the union of two events or the Addition Rule: P(A or B) = P(A) + P(B) P(A and B) ***Use this for both Mutually Exclusive and Inclusive events***
- 21. Examples 1. What is the probability of choosing a card from a deck of cards that is a club or a ten? P(choosing a club or a ten) = P(club) + P(ten) P(10 of clubs) = 13/52 + 4/52 1/52 = 16/52 = 4/13 or .308 The probability of choosing a club or a ten is 4/13 or 30.8%
- 22. 2. What is the probability of choosing a number from 1 to 10 that is less than 5 or odd? P(<5 or odd) = P(<5) + P(odd) P(<5 and odd) <5 = {1,2,3,4} odd = {1,3,5,7,9} = 4/10 + 5/10 2/10 = 7/10 The probability of choosing a number less than 5 or an odd number is 7/10 or 70%.
- 23. 3. A bag contains 26 tiles with a letter on each, one tile for each letter of the alphabet. What is the probability of reaching into the bag and randomly choosing a tile with one of the first 10 letters of the alphabet on it or randomly choosing a tile with a vowel on it? P(one of the first 10 letters or vowel) = P(one of the first 10 letters) + P(vowel) P(first 10 and vowel) = 10/26 + 5/26 3/26 = 12/26 or 6/13 The probability of choosing either one of the first 10 letters or a vowel is 6/13 or 46.2%
- 24. 4. A bag contains 26 tiles with a letter on each, one tile for each letter of the alphabet. What is the probability of reaching into the bag and randomly choosing a tile with one of the last 5 letters of the alphabet on it or randomly choosing a tile with a vowel on it? P(one of the last 5 letters or vowel) = P(one of the last 5 letters) + P(vowel) P(last 5 and vowel) = 5/26 + 5/26 0 = 10/26 or 5/13 The probability of choosing either one of the first 10 letters or a vowel is 5/13 or 38.5%
- 25. Assignment Mutually Exclusive & Inclusive Events Handout #1 18
- 26. End of Day
- 27. Conditional Probability Conditional probability questions are done the exact same way that regular probability question are done, except the denominator changes because we are looking at a smaller portion of the entire sample space. Example: A regular deck of cards has 52 cards in it. Find P(7) = Find P(face cards from the diamonds) = 4 52 3 13 The word from is often used in conditional probability
- 28. Two-way Tables A two way table is used to organize data when there are two different variables effecting the data. The variables are usually not independent of each other. P(A and B) = P(A) x P(B|A).
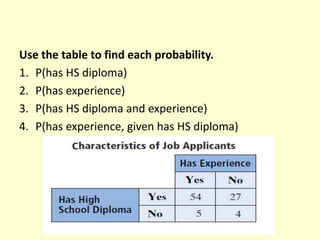
- 29. Use the table to find each probability. 1. P(has HS diploma) 2. P(has experience) 3. P(has HS diploma and experience) 4. P(has experience, given has HS diploma)
- 30. Make a tree diagram from the two-way table HS diploma Experience Experience
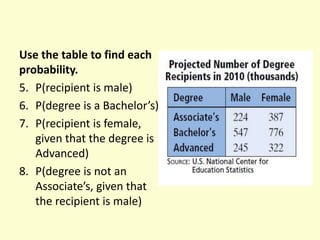
- 31. Use the table to find each probability. 5. P(recipient is male) 6. P(degree is a Bachelors) 7. P(recipient is female, given that the degree is Advanced) 8. P(degree is not an Associates, given that the recipient is male)
- 32. Two Way Tables Male Female Total Seniors 312 296 Juniors 301 334 Total a.) What is the probability a person from this group is male student? b.) What is the probability of selecting a student who is a senior from the female students? c.) What is the probability of selecting a student who is a female from the seniors? d.) What is the probability of selecting a student who is a junior and a male student? e.) What is the probability of selecting a student who is a junior or a male student?
- 33. End of Day 4
- 34. Factorials the way of multiplying all the integers from n to 1, it is denoted n! Example: 5! = 5x4x3x2x1 = 120 We use factorials when finding out how many possibilities there will be (the sample space) when we are using ALL of the choices. How many ways can you visit all of your four classes? 4 choices of where to go first 4x3x2x1=24 3 choices of where to go second or 2 choices of where to go third 4! = 24 1 choice of where to go last
- 35. Permutations a counting a procedure in which the order matters. We usually use permutations instead of factorials when we are using only part of the total number of items given. Example: You want to go visit 3 of the 8 teachers you had last year. How many different ways can you visit those teachers? P(8,3) or 8 nPr 3 = 336 Book notation for permutation Calculator notation for permutation
- 36. Combinations Combinations a counting a procedure in which the order does not matters. If you have three items A, B, C. Permutations Combinations ABC BAC CBA equals ABC ACB BCA CAB EXAMPLE: The Lottery has 50 numbers to choose from and you must pick 5 of them. You do not have to pick them in any order. How many different outcomes are there in this lottery? 50 nCr 5 = 2,118,760
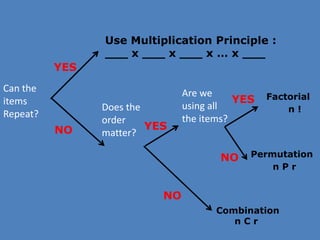
- 37. Can the items Repeat? YES NO Use Multiplication Principle : ___ x ___ x ___ x x ___ Does the order matter? YES NO Combination n C r Are we using all the items? YES NO Permutation n P r Factorial n !
- 38. End of Day 6
- 43. Binomial Probability The basic idea behind this is that events are either going to happen or they are NOT going happen. EXAMPLE: 3 question true/false quiz. How many different outcomes can the quiz have? What is the probability of each of the outcomes?
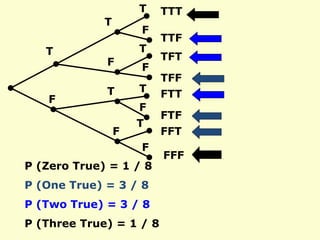
- 45. T T T T T T T F F F F F F F TTT FTF TFT TFF FTT TTF FFT FFF P (Zero True) = 1 / 8 P (One True) = 3 / 8 P (Two True) = 3 / 8 P (Three True) = 1 / 8
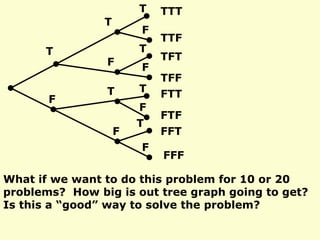
- 46. T T T T T T T F F F F F F F TTT FTF TFT TFF FTT TTF FFT FFF What if we want to do this problem for 10 or 20 problems? How big is out tree graph going to get? Is this a good way to solve the problem?
- 47. The answer is an overwhelming NO! A quiz with ten questions has 2 = 1024 different outcomes and a 20-question quiz has 2 = 1,048,576 outcomes. I do not think we want to draw those graphs. So we need to use the Binomial probability shortcut. 10 20
- 48. EXAMPLE: Same 3 question true/false Quiz using the shortcut Zero True : C(3,0) (1/2) (1/2) 0 3 Combinations of zero true answers in three questions Probability the answer is true (or event will happen) Probability the answer is false (or event wont happen) Always same Fractions add up to 1 but do not have to be the same Add up to 1st number
- 49. Zero True : C(3,0) (1/2) (1/2) (3nCr0) (1/2)0 (1/2)3 0 3 This is how it looks in the calculator Zero: (3 nCr 0) (1/2)^0 (1/2)^3 = .125 One: (3 nCr 1) (1/2)^1 (1/2)^2 = .375 Two: (3 nCr 2) (1/2)^2 (1/2)^1 = .375 Three: (3 nCr 3) (1/2)^3 (1/2)^0 = .125
- 50. EXAMPLE: You are rolling five dice at the same time. Make a probability distribution table for rolling a 4. Make sure you include each possible outcome.
- 51. Zero: (5 nCr 0) (1/6)^0 (5/6)^5 = .402 One: (5 nCr 1) (1/6)^1 (5/6)^4 = .402 Two: (5 nCr 2) (1/6)^2 (5/6)^3 = .161 Three: (5 nCr 3) (1/6)^3 (5/6)^2 = .032 Four: (5 nCr 4) (1/6)^4 (5/6)^1 = .003 Five: (5 nCr 5) (1/6)^5 (5/6)^0 = .0001
- 52. Expectations Page 324 Expectations give us the average winning losing amount per play of the game. Take the probability of each outcome times the payout for each outcome. (5 nCr 0) (1/6)^0 (5/6)^5 = .402 x -10 = -4.02 (5 nCr 1) (1/6)^1 (5/6)^4 = .402 x 3 = 1.21 (5 nCr 2) (1/6)^2 (5/6)^3 = .161 x 6 = .97 (5 nCr 3) (1/6)^3 (5/6)^2 = .032 x 9 = .29 (5 nCr 4) (1/6)^4 (5/6)^1 = .003 x 12 = .04 (5 nCr 5) (1/6)^5 (5/6)^0 = .0001 x 15 = .02 Then add all products together : -4.02+1.21+.97+.29+.04+.02 = -1.49 You get paid $3 for each time your number appears and lose $10 for your number not appearing at all.
- 53. End of Day 7