Ppt gerak harmonik sederhana
Download as PPTX, PDF
35 likes47,294 views
Dokumen tersebut membahas tentang gerak harmonik sederhana yang mencakup pengertian, jenis, contoh pada bandul dan pegas, hukum Hooke, periode dan frekuensi, simpangan, kecepatan, percepatan, serta energi pada gerak harmonik sederhana."
![Paralel
Jika rangkaian pegas ditarik dengan gaya sebesar F,
setiap pegas akan mengalami gaya tarik sebesar F1 dan
F2 , pertambahan panjang sebesar dan
. Secara umum, konstanta total pegas yang dirangkai
paralel dinyatakan dengan persamaan[5] :
ktotal = k1 + k2 + k3 +....+ kn, dengan kn = konstanta
pegas ke - n.](https://image.slidesharecdn.com/pptgerakharmoniksederhana-121225102749-phpapp01/85/Ppt-gerak-harmonik-sederhana-10-320.jpg)
Ppt gerak harmonik sederhana
- 1. Romi Ragubta Kurniawan 41612010038 Tri Desi Rahayu W 41612010041 Ahmad Jefriansyah 41612010033 Deni Ariyanto
- 2. Pengertian GHS Gerak harmonik sederhana adalah gerak bolak - balik benda melalui suatu titik keseimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan.
- 3. Jenis Gerak Harmonik Sederhana Gerak Harmonik Sederhana dapat dibedakan menjadi 2 bagian, yaitu : 1. Gerak Harmonik Sederhana (GHS) Linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas, dan sebagainya. 2. Gerak Harmonik Sederhana (GHS) Angular, misalnya gerak bandul/ bandul fisis, osilasi ayunan torsi, dan sebagainya.
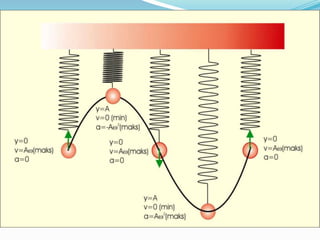
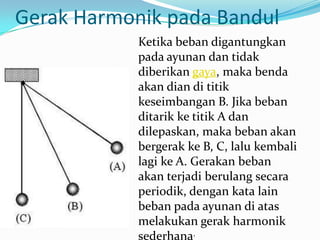
- 4. Gerak Harmonik pada Bandul Ketika beban digantungkan pada ayunan dan tidak diberikan gaya, maka benda akan dian di titik keseimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
- 5. GERAK HARMONIK PADA PEGAS Pegas merupakan suatu benda yang sering kita jumpai dalam berbagai aplikasi, dari saklar hingga sistem suspensi kendaraan. Pegas amat berguna karena memiliki kemampuan untuk direntang dan ditekan
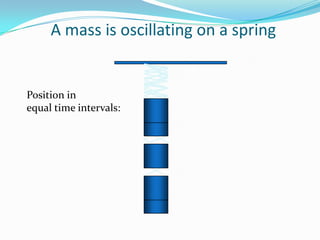
- 6. A mass is oscillating on a spring Position in equal time intervals:
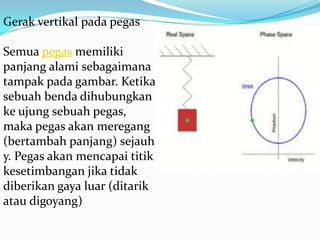
- 7. Gerak vertikal pada pegas Semua pegas memiliki panjang alami sebagaimana tampak pada gambar. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang)
- 8. Susunan Pegas Konstanta pegas dapat berubah nilainya, apabila pegas - pegas tersebut disusun menjadi rangkaian. Besar konstanta total rangkaian pegas bergantung pada jenis rangkaian pegas, yaitu rangkaian pegas seri atau paralel
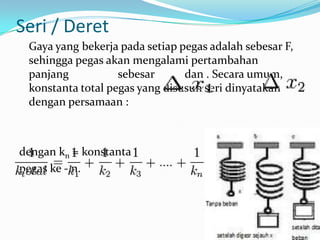
- 9. Seri / Deret Gaya yang bekerja pada setiap pegas adalah sebesar F, sehingga pegas akan mengalami pertambahan panjang sebesar dan . Secara umum, konstanta total pegas yang disusun seri dinyatakan dengan persamaan : dengan kn = konstanta pegas ke - n.
- 10. Paralel Jika rangkaian pegas ditarik dengan gaya sebesar F, setiap pegas akan mengalami gaya tarik sebesar F1 dan F2 , pertambahan panjang sebesar dan . Secara umum, konstanta total pegas yang dirangkai paralel dinyatakan dengan persamaan[5] : ktotal = k1 + k2 + k3 +....+ kn, dengan kn = konstanta pegas ke - n.
- 12. Contoh Soal Dua buah pegas identik dengan kostanta masing-masing sebesar 200 N/m disusun seri seperti terlihat pada gambar berikut. Beban m sebesar 2 kg digantungkan pada ujung bawah pegas. Tentukan periode sistem pegas tersebut! Pembahasan Gabungkan konstanta kedua pegas dengan susunan seri:
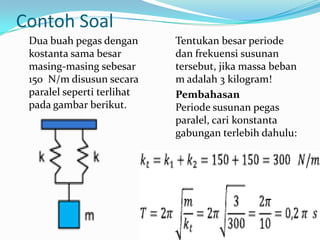
- 13. Contoh Soal Dua buah pegas dengan Tentukan besar periode kostanta sama besar dan frekuensi susunan masing-masing sebesar tersebut, jika massa beban 150 N/m disusun secara m adalah 3 kilogram! paralel seperti terlihat Pembahasan pada gambar berikut. Periode susunan pegas paralel, cari konstanta gabungan terlebih dahulu:
- 14. Gaya Pemulih Gaya pemulih dimiliki oleh setiap benda elastis yang terkena gaya sehingga benda elastis tersebut berubah bentuk. Gaya yang timbul pada benda elastis untuk menarik kembali benda yang melekat padanya di sebut gaya pemulih. Gaya Pemulih pada Pegas Pegas adalah salah satu contoh benda elastis. Oleh sifat elastisnya ini, suatu pegas yang diberi gaya tekan atau gaya regang akan kembali pada keadaan setimbangnya mula- mula apabila gaya yang bekerja padanya dihilangkan. Gaya pemulih pada pegas banyak dimanfaatkan dalam bidang teknik dan kehidupan sehari- hari. Misalnya di dalam shockbreaker dan springbed. Sebuah pegas berfungsi meredam getaran saat roda kendaraan melewati jalan yang tidak rata. Pegas - pegas yang tersusun di dalam springbed akan memberikan kenyamanan saat orang tidur
- 15. Hukum Hooke Jika gaya yang bekerja pada sebuah pegas dihilangkan, pegas tersebut akan kembali pada keadaan semula. Robert Hooke, ilmuwan berkebangsaan Inggris menyimpulkan bahwa sifat elastis pegas tersebut ada batasnya dan besar gaya pegas sebanding dengan pertambahan panjang pegas. Dari penelitian yang dilakukan, didapatkan bahwa besar gaya pegas pemulih sebanding dengan pertambahan panjang pegas. Secara matematis, dapat dituliskan sebagai: , dengan k = tetapan pegas (N / m) Tanda (-) diberikan karena arah gaya pemulih pada pegas berlawanan dengan arah gerak pegas tersebut.
- 16. Gaya Pemulih pada Gerak Harmonik Sederhana Gaya Pemulih pada Pegas k = konstanta pegas (N/m) y = simpangan (m) Gaya Pemulih pada Ayunan Bandul Sederhana m = massa benda (kg) g = percepatan gravitasi (m/s2)
- 17. Periode dan Frekuensi Periode adalah waktu yg diperlukan untuk melakukan satu kali gerak bolak-balik. Frekuensi adalah banyaknya getaran yang dilakukan dalam waktu 1 detik. Untuk pegas yg memiliki konstanta gaya k yg bergetar karena adanya beban bermassa m, periode getarnya adalah
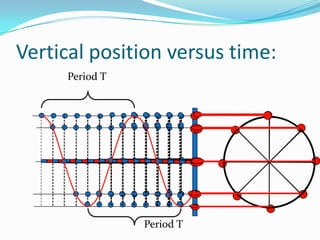
- 18. Vertical position versus time: Period T Period T
- 19. Sedangkan pada ayunan bandul sederhana, jika panjang tali adalah l, maka periodenya adalah Keterangan : f = frekuensi pegas (Hz) T = periode pegas (sekon) k = konstanta pegas (N/m) m = massa (kg)
- 20. Contoh Soal Sebuah bandul matematis memiliki panjang tali 64 cm dan beban massa sebesar 200 gram. Tentukan periode getaran bandul matematis tersebut, gunakan percepatan gravitasi bumi g = 10 m/s2 Pembahasan Periode ayunan sederhana: Dari rumus periode getaran ayunan sederhana: Sehingga: Catatan: Massa beban tidak mempengaruhi periode atau frekuensi dari ayunan sederhana (bandul matematis, conis).
- 21. Contoh Soal Sebuah beban bermassa 250 gram digantung dengan sebuah pegas yang memiliki kontanta 100 N/m kemudian disimpangkan hingga terjadi getaran selaras. Tentukan periode getarannya! Pembahasan Diketahui: k = 100 N/m m = 250 g = 0,25 kg T = .....
- 22. Dari rumus periode getaran sistem pegas: Sehingga:
- 23. Simpangan Gerak Harmonik Sederhana y = simpangan (m) A = amplitudo (m) = kecepatan sudut (rad/s) f = frekuensi (Hz) t = waktu tempuh (s) Jika pada saat awal benda pada posisi 慮0, maka Besar sudut (t+慮0) disebut sudut fase (慮), sehingga disebut fase getaran dan disebut beda fase.
- 24. Contoh Soal Sebuah benda bergetar hingga membentuk suatu gerak harmonis dengan persamaan y = 0,04 sin 20 t dengan y adalah simpangan dalam satuan meter, t adalah waktu dalam satuan sekon. Tentukan beberapa besaran dari persamaan getaran harmonis tersebut: a) amplitudo b) frekuensi c) periode d) simpangan maksimum e) simpangan saat t = 1/60 sekon f) simpangan saat sudut fasenya 45属 g) sudut fase saat simpangannya 0,02 meter
- 25. Pembahasan Pola persamaan simpangan gerak harmonik diatas adalah periode atau T c) y = A sin t T = 1/f T = 1/10 = 0,1 s = 2 f atau 2 = _____ d) simpangan maksimum atau T ymaks a) amplitudo atau A y = A sin t y = 0,04 sin 20 t y = ymaks sin t y = 0,04 sin 20 t A = 0,04 meter b) frekuensi atau f y = ymaks sin t y = 0,04 sin 20 t ymaks = 0,04 m = 20 2f = 20 (Simpangan maksimum tidak lain adalah amplitudo)
- 26. e) simpangan saat t = 1/60 sekon y = 0,04 sin 20 t y = 0,04 sin 20 (1/60) y = 0,04 sin 1/3 y = 0,04 sin 60属 = 0,04 1/23 = 0,02 3 m f) simpangan saat sudut fasenya 45属 y = A sin t y = A sin 慮 dimana 慮 adalah sudut fase, 慮 = t y = 0,04 sin 慮 y = 0,04 sin 45属 = 0,04 (0,52) = 0,022 m g) sudut fase saat simpangannya 0,02 meter y = 0,04 sin 20 t y = 0,04 sin 慮 0,02 = 0,04 sin 慮 sin 慮 = 1/2 慮 = 30属
- 27. Contoh Soal 2 Diberikan sebuah persamaan simpangan gerak harmonik y = 0,04 sin 100 t Tentukan: a) persamaan kecepatan b) kecepatan maksimum c) persamaan percepatan Pembahasan a) persamaan kecepatan Berikut berurutan rumus simpangan, kecepatan dan percepatan:
- 28. Pembahasan sehingga: a) persamaan kecepatan 僚 = A cos t Berikut berurutan rumus 僚 = (100)(0,04) cos 100 t simpangan, kecepatan dan 僚 = 4 cos 100 t percepatan: y = A sin t b) kecepatan maksimum 僚 = A cos t 僚 = A cos t a = 2 A sin t 僚 = 僚maks cos t 僚maks = A Ket: y = simpangan (m) 僚 = 4 cos 100 t 僚 = kecepatan (m/s) a = percepatan (m/s2) 僚maks = 4 m/s Dari y = 0,04 sin 100 t c) persamaan percepatan = 100 rad/s a = 2 A sin t A = 0,04 m a = (100)2 (0,04) sin 100 t a = 400 sin 100 t
- 29. KECEPATAN (v) Jika simpangan menunjukkan posisi suatu benda, maka kecepatan merupakan turunan pertama dari posisi. Hubungan kecepatan dengan simpangan harmonik
- 30. Contoh Soal Sebuah balok bermassa 0,5 kg dihubungkan dengan Periode getaran pegas : sebuah pegas ringan dengan konstanta 200 N/m. T = 2 (m/k) Kemudian sistem tersebut T = 2 (0,5/200) = 2(1/400) berosilasi harmonis. Jika = 2 (1/20) = 0,1 sekon diketahui simpangan maksimumnya adalah 3 cm, maka kecepatan maksimum vmaks = A adalah.... A. 0,1 m/s B. 0,6 m/s 2 C. 1 m/s vmaks= ____ x A D. 1,5 m/s E. 2 m/s T Pembahasan 2 Data : m = 0,5 kg vmaks = ______ x (0,03) = 0,6 k = 200 N/m m/s ymaks = A = 3 cm = 0,03 m 0,1 vmaks = ......
- 31. PERCEPATAN (a) Jika simpangan menunjukkan posisi suatu benda, maka kecepatan merupakan turunan pertama dari kecepatan terhadap waktu. Hubungan percepatan dengan simpangan harmonik Ket: : kecepatan sudut (rad/s) A : amplitudo (m) a : percepatan
- 32. Energi pada Gerak Harmonik Sederhanabenda yg melakukan gerak harmonik Energi kinetik sederhana, misalnya pegas, adalah Karena k = m2, diperoleh Energi potensial elastis yg tersimpan di dalam pegas untuk setiap perpanjanganya adalah
- 33. Jika gesekan diabaikan, energi total atau energi mekanik pada getaran pegas adalah Keterangan: Em : Energi Mekanik Ep : Energi Potensial Ek : Energi Kinetik A : Ampitudo m : Massa : kecepatan sudut (rad/s)
- 34. Contoh Soal Sebuah benda yang massanya 200 gram bergetar harmonik dengan periode 0,2 sekon dan amplitudo 2 cm. Tentukan : a) besar energi kinetik saat simpangannya 1 cm b) besar energi potensial saat simpangannya 1 cm c) besar energi total Pembahasan
- 35. Data dari soal: m = 200 g = 0,2 kg T = 0,2 s f = 5 Hz A = 2 cm = 0,02 m = 2 x 10-2 m a) besar energi kinetik saat simpangannya 1 cm y = 1 cm = 0,01 m = 10-2 m Ek = .... b) besar energi potensial saat simpangannya 1 cm c) besar energi total
- 36. Contoh Soal Tentukan besarnya sudut fase saat : a) energi kinetik benda yang bergetar sama dengan energi potensialnya b) energi kinetik benda yang bergetar sama dengan sepertiga energi potensialnya Pembahasan a) energi kinetik benda yang bergetar sama dengan energi potensialnya Ek = Ep 1/2 m僚2 = 1/2 ky2 1/2 m ( A cos t)2 = 1/2 m2 (A sin t)2 1/2 m 2 A2 cos2 t = 1/2 m2 A2 sin2 t cos2 t = sin2 t cos t = sin t tan t = 1 t = 45属
- 37. Energi kinetik benda yang bergetar sama dengan energi potensialnya saat sudut fasenya 45属 b) energi kinetik benda yang bergetar sama dengan sepertiga energi potensialnya Ek = 1/3 Ep 1/2 m僚2 =1/3 x 1/2 ky2 1/2 m ( A cos t)2 = 1/3 x 1/2 m2 (A sin t)2 1/2 m 2 A2 cos2 t = 1/3 x 1/2 m2 A2 sin2 t cos2 t = 1/3 sin2 t cos t = 1/3 sin t sin t / cos t = 3 tan t = 3 t = 60属 Energi kinetik benda yang bergetar sama dengan sepertiga energi potensialnya saat sudut fasenya 60属