Presentasi.pptx
- 1. MATERI SUDUT ŌĆó Presentasi kelompok 3 ŌĆó Matematika ŌĆó Nama kelompok : Ari,Dio.Tika, ŌĆó Aprilia,Yuka,Ernest,sarul
- 2. PENGERTIAN SUDUT Sudut merupakan sebuah daerah yang terbentuk dari dua buah sinar garis yang bertemu di satu titik pangkal yang sama. Titik temu dua sinar garis tersebut dinamakan titik vertex. Dalam bahasa matematika, sudut dituliskan atau disimbolkan dengan tanda ŌĆ£ŌłĀŌĆØ.
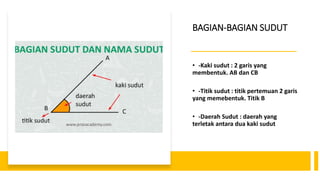
- 3. BAGIAN-BAGIAN SUDUT ŌĆó -Kaki sudut : 2 garis yang membentuk. AB dan CB ŌĆó -Titik sudut : titik pertemuan 2 garis yang memebentuk. Titik B ŌĆó -Daerah Sudut : daerah yang terletak antara dua kaki sudut
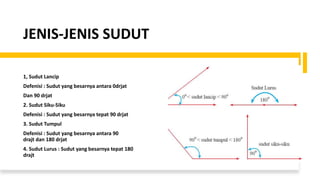
- 4. JENIS-JENIS SUDUT 1, Sudut Lancip Defenisi : Sudut yang besarnya antara 0drjat Dan 90 drjat 2. Sudut Siku-Siku Defenisi : Sudut yang besarnya tepat 90 drjat 3. Sudut Tumpul Defenisi : Sudut yang besarnya antara 90 drajt dan 180 drjat 4. Sudut Lurus : Sudut yang besarnya tepat 180 drajt
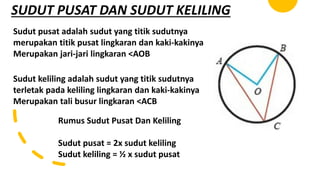
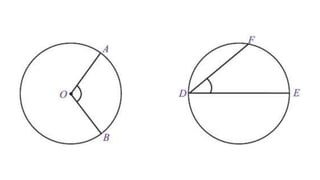
- 5. SUDUT PUSAT DAN SUDUT KELILING Sudut pusat adalah sudut yang titik sudutnya merupakan titik pusat lingkaran dan kaki-kakinya Merupakan jari-jari lingkaran <AOB Sudut keliling adalah sudut yang titik sudutnya terletak pada keliling lingkaran dan kaki-kakinya Merupakan tali busur lingkaran <ACB Rumus Sudut Pusat Dan Keliling Sudut pusat = 2x sudut keliling Sudut keliling = ┬Į x sudut pusat
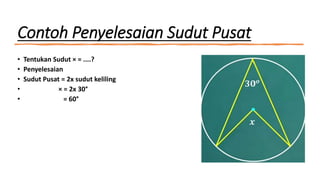
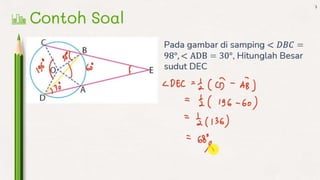
- 6. Contoh Penyelesaian Sudut Pusat ŌĆó Tentukan Sudut ├Ś = ....? ŌĆó Penyelesaian ŌĆó Sudut Pusat = 2x sudut keliling ŌĆó ├Ś = 2x 30┬░ ŌĆó = 60┬░
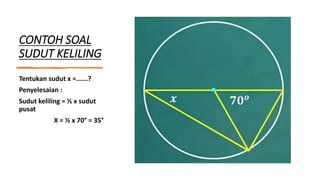
- 7. CONTOH SOAL SUDUT KELILING Tentukan sudut x =......? Penyelesaian : Sudut keliling = ┬Į x sudut pusat X = ┬Į x 70┬░ = 35┬░
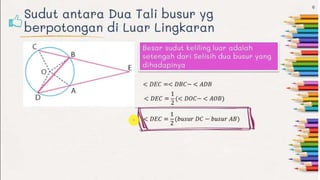
- 8. SUDUT ANTARA 2 TALI BUSUR ŌĆó Tali busur adalah sebuah ruas garis dari dua titik yang terletak pada tepi lingkaran. Perpotongan dua tali busur menghasilkan sudut antara dua tali busur. Ada dua jenis sudut hasil perpotongan dua tali busur yaitu sudut antara dua tali busur yang berpotongan di dalam dan luar lingkaran. Besar sudut antara dua tali busur dapat diketahui melalui sebuah rumus yang diperoleh dari karakterisir besar sudut pusat dan keliling pada lingkaran.
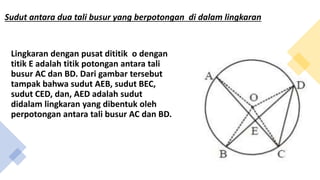
- 9. Sudut Antara Dua Tali Busur yang Berpotongan di Dalam Lingkaran
- 10. Lingkaran dengan pusat dititik o dengan titik E adalah titik potongan antara tali busur AC dan BD. Dari gambar tersebut tampak bahwa sudut AEB, sudut BEC, sudut CED, dan, AED adalah sudut didalam lingkaran yang dibentuk oleh perpotongan antara tali busur AC dan BD. Sudut antara dua tali busur yang berpotongan di dalam lingkaran
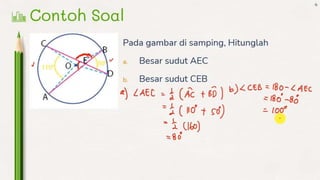
- 12. Jika besar ŌłĀAOC = 65┬░ dan ŌłĀBOD = 140┬░, tentukan besar ŌłĀAEC dan besar ŌłĀBEC Penyelesaian: ŌłĀAEC = ┬Į x (ŌłĀAOC + ŌłĀBOD) ŌłĀAEC = ┬Į x (65┬░ + 140┬░) ŌłĀAEC = ┬Į x 205┬░ ŌłĀAEC = 102,5┬░ ŌłĀBEC + ŌłĀ AEC = 180┬░ (sudut berpelurus) ŌłĀ BEC + 102,5┬░= 180┬░ ŌłĀ BEC = 180┬░ - 102,5┬░ ŌłĀ BEC = 77,5┬░