Presentation on Bayesian Structure from Motion
1 like547 views
The paper presents a hierarchical Bayesian model for non-rigid structure from motion that estimates shape and motion from 2D tracking points. The model represents shapes as a combination of basic shapes plus noise and incorporates a dynamic model to represent shape variations over time. Expectation-maximization is used to estimate model parameters, and the model is shown to be more robust to noise than previous approaches.
Presentation on Bayesian Structure from Motion
- 1. Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors Lorenzo Torresani Aaron Karper paper by Aaron Hertzmann Christoph Bregler October 22, 2013 paper: May 2008 Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 1 / 15
- 2. 1 Goal 2 Primer in Bayesian statistics 3 Model re鍖nement: PPCA further re鍖nement: Dynamic model 4 Solving for the model 5 Evaluation 6 Questions Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 2 / 15
- 3. Goal Goal Given a series of tracking points pj R2 , we want to estimate shape of the tracked object, pose of the tracked object, movement of the camera, be robust to missing tracking points (e.g. because of occlusion), be robust to noisy coordinates of tracking points. The main example is tracking the movement of a face. Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 3 / 15
- 4. Primer in Bayesian statistics Primer in Bayesian statistics probability as a measure of (un-)certainty. we are certain about our data we are uncertain about how it was produced. Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 4 / 15
- 5. Primer in Bayesian statistics Primer in Bayesian statistics prior p(M|D) = likelihood p(M) p(D|M) p(M) p(D|M) p(D) posterior model evidence M is a model and is usually described by some parameters. D is the observed data. Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 5 / 15
- 6. Primer in Bayesian statistics Primer in Bayesian statistics A hierarchical model can be built with hidden/latent variables Z : D Z 慮 p(慮|D) p(D|慮) p(慮) = p(D|Z ) p(Z |慮) p(慮) D Z 慮 means p(D|慮, Z ) = p(D|Z )1 1 The variables form a Markov chain Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 6 / 15
- 7. Primer in Bayesian statistics Primer in Bayesian statistics estimation (distribution) for all variables. marginalizing for better estimates of remaining variables p(慮|X ) = p(慮|X , Y = y ) dy Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 7 / 15
- 8. Model Model pj,t = cj Rt (sj,t + dt ) + nj,t pj,t projected 2d point. cj scaling. Rj orthographic projection. sj,t shape of object. dt movement of object. nj,t noise in recognition N (0, ). Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 8 / 15
- 9. Model Model Estimate all points at the same time: pt = Gt (st + Dt ) + Nt Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with Hierarchical Priors 2008 October 22, 2013paper: May 9 / 15
- 10. Model Model st = 俗 + Vt zt + mt s Vt basic shapes. zt description of object in terms of basic shapes. mt noise in model. Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 10 / 15
- 11. Model re鍖nement: PPCA Model re鍖nement: PPCA Vt zt describes a shape in low dimensions and blows it up into k points in R3 . zt N (0, I) More restricted than PCA, because it assumes shapes vary only a little over the basic shapes. zt are marginalized out. Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 11 / 15
- 12. Model further re鍖nement: Dynamic model Model further re鍖nement: Dynamic model Assume time line: z1 N (0, I) zt = 陸 zt1 + vt vt N (0, Q) Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 12 / 15
- 13. Solving for the model Solving for the model Squared loss for model to observed mathbfp. EM2 to 鍖nd maximum likelihood. 2 estimate-maximize, alternate between estimating variables in model and maximizing Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 13 / 15
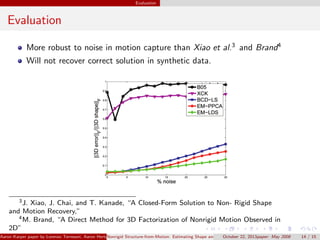
- 14. Evaluation Evaluation More robust to noise in motion capture than Xiao et al.3 and Brand4 Will not recover correct solution in synthetic data. 3 J. Xiao, J. Chai, and T. Kanade, A Closed-Form Solution to Non- Rigid Shape and Motion Recovery, 4 M. Brand, A Direct Method for 3D Factorization of Nonrigid Motion Observed in 2D Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 14 / 15
- 15. Questions Questions Aaron Karper paper by Lorenzo Torresani, Aaron Hertzmann, Christoph Bregler () Nonrigid Structure-from-Motion: Estimating Shape and Motion with22, 2013paper: May 2008 October Hierarchical Priors 15 / 15