�ݺ�ߣ

POWER SYSTEM
STATE ESTIMATION
Presentation by
Ashwani Kumar Chandel
Associate Professor
NIT-Hamirpur

Presentation Outline
• Introduction
• Power System State Estimation
• Solution Methodologies
• Weighted Least Square State Estimator
• Bad Data Processing
• Conclusion
• References

Introduction
• Transmission system is under stress.
 Generation and loading are constantly increasing.
 Capacity of transmission lines has not increased
proportionally.
 Therefore the transmission system must operate with ever
decreasing margin from its maximum capacity.
• Operators need reliable information to operate.
 Need to have more confidence in the values of certain
variables of interest than direct measurement can typically
provide.
 Information delivery needs to be sufficiently robust so that
it is available even if key measurements are missing.
• Interconnected power networks have become more complex.
• The task of securely operating the system has become more
difficult.

Difficulties mitigated through use
of state estimation
• Variables of interest are indicative of:
 Margins to operating limits
 Health of equipment
 Required operator action
• State estimators allow the calculation of these variables
of interest with high confidence despite:
 measurements that are corrupted by noise
 measurements that may be missing or grossly
inaccurate

Objectives of State Estimation
• Objectives:
 To provide a view of real-time power system conditions
 Real-time data primarily come from SCADA
 SE supplements SCADA data: filter, fill, smooth.
 To provide a consistent representation for power
system security analysis
• On-line dispatcher power flow
• Contingency Analysis
• Load Frequency Control
 To provide diagnostics for modeling & maintenance

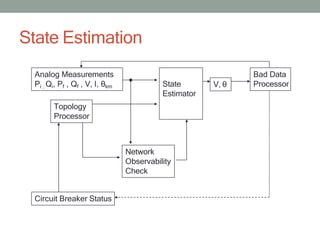
Power System State Estimation
• To obtain the best estimate of the state of the system
based on a set of measurements of the model of the
system.
• The state estimator uses
 Set of measurements available from PMUs
 System configuration supplied by the topological
processor,
 Network parameters such as line impedances as
input.
 Execution parameters (dynamic weight-
adjustments…)

Power System State Estimation (Cont.,)
• The state estimator provides
 Bus voltages, branch flows, …(state variables)
 Measurement error processing results
 Provide an estimate for all metered
quantities.
and unmetered
 Filter out small errors due to model approximations and
measurement inaccuracies;
 Detect and identify discordant measurements, the so-
called bad data.

State Estimation
Analog Measurements
Pi , Qi, Pf , Qf , V, I, θkm
Circuit Breaker Status
State
Estimator
Bad Data
Processor
Network
Observability
Check
Topology
Processor
V, θ

• The state (x) is defined as the voltage magnitude and
angle at each bus
i
Vi Vej i
~
x [V1,V2,...,Vn , 1,..., b ]
Measurement
Model: h(x)
• All variables of interest can be calculated from the state
and the measurement mode. z = h(x)
I12
P12
V1

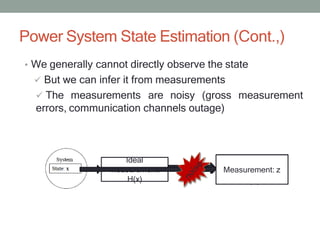
• We generally cannot directly observe the state
 But we can infer it from measurements
 The measurements are noisy (gross measurement
errors, communication channels outage)
Ideal
measurement:
H(x)
Noisy
Measurements
z=h(x)+e
Measurement: z

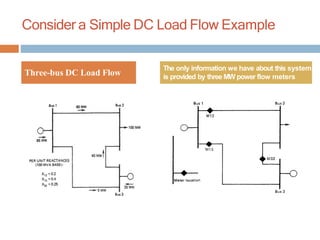
Consider a Simple DC Load Flow Example
Three-bus DC Load Flow
The only information we have about this system
is provided by three MW power flow meters

(Cont.,)
 Only two of these meter readings are required to calculate the bus
phase angles and all load and generation values fully
Now calculating the angles, considering third bus as swing bus we get
M13
M32
5MW 0.05pu
40MW 0.40pu
13 1 3 13
13
32 3 2 32
23
1
(
f ) M 0.05pu
x
1
(
f ) M 0.40pu
x
1
2
0.02rad
0.10rad

Case with all meters have small errors
s,
If we use only the M13 and M32 reading
as before, then the phase angles will be:
This results in the system flows as shown in
Figure . Note that the predicted flows match at
M13, and M32 but the flow on line 1-2 does not
match the reading of 62 MW from M12.
1
2
3
0.024rad
0.0925rad
0rad(still assumed to equal zero)
M12
M13
M32
62MW 0.62pu
6MW 0.06pu
37MW 0.37pu

• The only thing we know about the power system comes to
us from the measurements so we must use the
measurements to estimate system conditions.
• Measurements were used to calculate the angles at
different buses by which all unmeasured power flows,
loads, and generations can be calculated.
• We call voltage angles as the state variables for the three-
bus system since knowing them allows all other quantities
to be calculated
• If we can use measurements to estimate the “states” of
the power system, then we can go on to calculate any
power flows, generation, loads, and so forth that we
desire.

State Estimation: determining our best guess at the state
• We need to generate the best guess for the state given
the noisy measurements we have available.
• This leads to the problem how to formulate a “best”
estimate of the unknown parameters given the available
measurement.
• The traditional methods most commonly encountered
criteria are
 The Maximum likelihood criterion
 The weighted least-squares criterion.
• Non traditional methods like
 Evolutionary optimization techniques like Genetic
Algorithms, Differential Evolution Algorithms etc.,

Solution Methodologies
Weighted Least Square (WLS)method:
Minimizes the weighted sum of squares of the difference between
measured and calculated values .
 In weighted least square method, the objective function „f‟
minimized is given by
to be
Iteratively Reweighted Least Square
Value (WLAV)method:
(IRLS)Weighted Least Absolute
 Minimizes the weighted sum of the absolute value of difference
between measured and calculated values.
The objective function to be minimized is given by
m
| pi|
i 1
The weights get updated in every iteration.
m
i
i 1
2
i
1
e2

(Cont.,)
Least Absolute Value(LAV) method:
 Minimizes the objective function which is the sum of absolute
value of difference between measured and calculated values.
The objective function „g‟to be minimized is given by g=
m
Subject to constraint zi= hi(x) + ei
Where, σ2 = variance of the measurement
W=weight of the measurement (reciprocal
measurement)
of variance of the
ei = zi-hi(x), i=1, 2, 3 ….m.
h(x) = Measurement function, x = state variables and Z= Measured
Value
m=number of measurements
i 1
W | h (x)-z |
i i i

(Cont.,)
• The measurements are assumed to be in error: that is, the
value obtained from the measurement device is close to
the true value of the parameter being measured but differs
by an unknown error.
• If Zmeas be the value of a measurement as received from a
measurement device.
• If Ztrue be the true value of the quantity being measured.
• Finally, let η be the random measurement error.
Then mathematically it is expressed as
Zmeas
Ztrue

(Cont.,)
•
1
PDF( ) exp( 2
/ 2 2
)
2

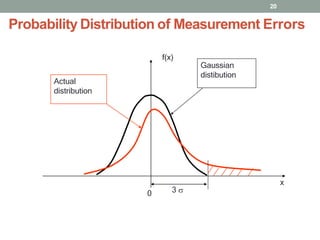
20
Probability Distribution of Measurement Errors
3
f(x)
x
0
Gaussian
distibution
Actual
distribution

Weighted least Squares-State Estimator
• The problem of state estimation is to determine the
estimate that best fits the measurement model .
• The static-state of an M bus electric power network is
denoted by x, a vector of dimension n=2M-1, comprised of
M bus voltages and M-1 bus voltage angles (slack bus is
taken as reference).
• The state estimation problem can be formulated as a
minimization of the weighted least-squares (WLS)
•
m
i 1
(z h (x))2
i i
2
i
function problem.
min J(x)=

(Cont.,)
• This represents the summation of the squares of the
measurement residuals weighted by their respective
measurement error covariance.
• where, z is measurement vector.
h(x) is measurement matrix.
m is number of measurements.
σ2 is the variance of measurement.
x is a vector of unknown variables to be estimated.
• The problem defined is solved as an unconstrained
minimization problem.
• Efficient solution of unconstrained minimization problems
relies heavily on Newton‟s method.

(Cont.,)
• The type of Newton‟s method of most interest here is the
Gauss-Newton method.
• In this method the nonlinear vector function is linearized
using Taylor series expansion
h(x x) h(x) H(x) x
• where, the Jacobian matrix H(x) is defined as:
h(x)
H(x)
x
• Then the linearized least-squares objective function is
given by
J( x) 1
(z h(x) H(x) x)T
R 1
(z h(x) H(x) x)
2

(Cont.,)
• where, R is a weighting matrix whose diagonal elements
are often chosen as measurement error variance, i.e.,
2
1
2
m
R ⋱
H(x) x)
J( x)
1
(e(x) H(x) x)T
R 1
(e(x)
2
• where, e=z-h(x) is the residual vector.

(Cont.,)
•
J( x)
HT
R 1
(e H x) 0
x
HT
R 1
H x HT
R 1
e
G x HT
R 1
e

Weighted Least Squares-Example
•
est
1
est
2
xest

(Cont.,)
• To derive the [H] matrix, we need to write the measurements
1
as a function of the state variables 2 . These functions
are written in per unit as
and
1 2 1 2
1 3 1
32 32 3 2 2
M12 f12
1
( ) 5 5
0.2
M13 f13
1
( ) 2.5
0.4
1
M f ( ) 4
0.25

(Cont.,)
•
[H]
5 5
2.5 0
0 4
2
M12
2
M12
2
M13
2
M13
2
M32
2
M32
0.0001
R 0.0001
0.0001

(Cont.,)
•
1
1
est
1
est
2
1
0.0001
0.0001
0.0001
5 5
2.5 0
0 4
0.0001
0.0001
5 2.5 0
-5 0 -4
5 2.5 0
-5 0 -4
0.62
0.06
0.0001 0.37

(Cont.,)
• We get
• From the estimated phase angles, we can calculate the
power flowing in each transmission line and the net
generation or load at each bus.
est
1
est
2
0.028571
0.094286
(0.06 (2.5 ))2
(0.37 (4 ))2
J( 1, 2 ) 1
0.0001
2
0.0001
(0.62 (5 5 ))2
1 2
0.0001
2.14

Solution of the weighted least square example

Bad Data Processing
• One of the essential functions of a state estimator is to
detect measurement errors, and to identify and eliminate
them if possible.
• Measurements may contain errors due to
 Random errors usually exist in measurements due to
the finite accuracy of the meters
 Telecommunication medium.
• Bad data may appear in several different ways depending
upon the type, location and number of measurements that
are in error. They can be broadly classified as:
 Single bad data: Only one of the measurements in
the entire system will have a large error
• Multiple bad data: More than one measurement will be in
error

(Cont.,)
• Critical measurement: A critical measurement is the one whose
elimination from the measurement set will result in an unobservable
system. The measurement residual of a critical measurement will
always be zero.
• A system is said to be observable if all the state variables can be
calculated with available set of measurements.
• Redundant measurement: A redundant measurement is a
measurement which is not critical. Only redundant measurements
may have nonzero measurement residuals.
• Critical pair: Two redundant measurements whose
removal from the measurement set will make
unobservable.
simultaneous
the system

(Cont.,)
• When using the WLS estimation method, detection and
identification of bad data are done only after the estimation
process by processing the measurement residuals.
J x (z h(x))'W z h(x)
• The condition of optimality is that the gradient of J(x) vanishes
at the optimal solution x, i.e.,
• An estimate z of the measurem ent vector z is given by
• The vector of residuals is defined as e = z - Hx; an estimate of
e is given by
GX
‸ H1
WZ 0 X
‸ G 1
H1
WZ
Z
‸ HX
e
‸ z h(x)

Bad Data Detection and Identification
• Detection refers to the determination of whether or not the
measurement set contains any bad data.
• Identification is the procedure of finding out which specific
measurements actually contain bad data.
• Detection and identification of bad data depends on the
configuration of the overall measurement set in a given
power system.
• Bad data can be detected if removal of the corresponding
measurement does not render the system unobservable.
• A single measurement containing bad data can be
identified if and only if:
 it is not critical and
 it does not belong to a critical pair

Bad Data Detection
•
N
i
i 1
Y X2
2
k
Y ~

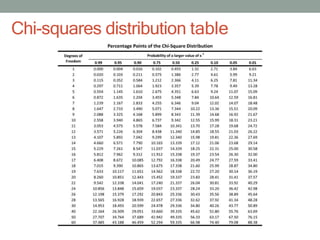
Chi-square probability density function

Chi-squares distribution table

(Cont.,)
• The degrees of freedom k, represents the number of
independent variables in the sum of squares.
• Now, let us consider the function f(x), written in terms of the
• where e is theithmeasurement error, Rii is the diagonal entry of
the measurement error covariance matrix and m is the total
number of measurements.
• Then, f(x) will have a chi-square distribution with at most (m -
n) degrees of freedom.
where, m is number of measurements.
n is number of state variables.
2
m m
2
1 2 N
i
i 1 i 1
e
measurement errors:
m
f(x)
i 1
Rii ei ei
Rii

Steps to detection of bad data
•
m
i i
j 1
f e2
/ 2
.

Bad Data Identification
•
ii
(zi zi ) / R'
ii
R'
(I HG 1
HT
R 1
)R

Steps to Bad Data Identification
•
i
ii
ei
eN
R'
i=1,2,...m

Cont.,
• Measurement equations characterizing the meter
readings are found by adding errors terms to the system
model. We obtain
1 1 2 1
2 1 2 2
3 1 2 3
4 1 2 4
5
x
1
x
z e
8 8
z e
1
x
8
x
8 8
z e
z e
3
x
1
x
8 8
1
x
3
x
8 8

(Cont.,)
• Forming the H matrix we get
0.625 0.125
0.125 0.625
0.375 0.125
0.125 0.375
H
100 0 0 0
0 100 0 0
0 0 50 0
0 0 0 50
W
9.01
3.02
6.98
5.01
z

(Cont.,)
• Solving for state estimates i.e.,
• We get
G 1
HT
Wz
V1
V2
16.0072V
8.0261V
V1
V2

•
(Const.,)
9.00123A
3.01544A
7.00596V
5.01070V
z1
z2
z3
z4

(Cont.,)
•
9.01 9.00123 0.00877A
3.02 3.01544 0.00456A
6.98 7.00596 0.02596V
5.01 5.01070 0.00070V
e1
e2
e3
e4

(Cont.,)
•
4
i
2
i
f e2
/ 100(0.00877)2
100(0.00456)2
50(0.02596)2
50(0.00070)2
j 1
0.043507

(Cont.,)
•
1 2 3 4
[z z z z ]T
[9.01A 3.02A 6.98V 4.40V]T
[e e e e ]T
[9.01A 3.02A 6.98V 4.40V]T
1 2 3 4
4
i
2
i
f e2
/ 100(0.06228)2
100(0.15439)2
50(0.05965)2
50(0.49298)2
j 1
15.1009

(Cont.,)
•
ii
R'
(I HG 1
HT
R 1
)R
i
ii
ei
eN
R'
i=1,2,...m

(Cont.,)
•
11
22
33
44
e1 0.06228
1.4178
R'
e2
3.5144
R'
e3
0.4695
(1 0.807) 0.01
0.15439
(1 0.807) 0.01
0.05965
(1 0.193) 0.02
R'
e4 0.49298
3.8804
(1 0.193) 0.02
R'

Conclusion
• Real time monitoring and control of power systems is
extremely important for an efficient and reliable operation
of a power system.
• Sate estimation forms the backbone for the real time
monitoring and control functions.
• In this environment, a real-time model is extracted at
intervals from snapshots of real-time measurements.
• Estimate the nodal voltage magnitudes and phase angles
together with the parameters of the lines.
• State estimation results can be improved by using
accurate measurements like phasor measurement units.
• Traditional state estimation and bad data processing is
reviewed.

References
• F. C. Schweppe and J. Wildes, “Power system static state estimation, part I: exact
model,” IEEE Trans. Power Apparatus and Systems, vol. PAS-89, pp. 120-125,
Jan. 1970.
• R. E. Tinney W. F. Tinney, and J. Peschon, “State estimation in power systems,
part i: theory and feasibility,” IEEE Trans. Power Apparatus and Systems, vol.
PAS-89, pp. 345-352, Mar. 1970.
• F. C. Schweppe and D. B. Rom, “Power system static-state estimation, part ii:
approximate model,” IEEE Trans. Power Apparatus and Systems, vol. PAS-89,
pp.125-130, Jan. 1970.
• F. F. Wu, “Power System State Estimation,” International Journal of Electrical
Power and Energy Systems, vol. 12, Issue. 2, pp. 80-87, Apr. 1990.
• Ali Abur and Antonio Gomez Exposito. (2004, April). Power System State
(1st
Estimation Theory and Implementation ed.) [Online]. Available:
http://www.books.google.com.
• Allen J wood and Bruce F Wollenberg. (1996, February 6). Power Generation,
Operation, and Control (2nd ed.) [Online]. Available:
http://www.books.google.com.

�ݺ�ߣ

Presentation on the power quality and accuracy

Recommended

More Related Content

Similar to Presentation on the power quality and accuracy (20)

Recently uploaded (20)

Presentation on the power quality and accuracy