Number System
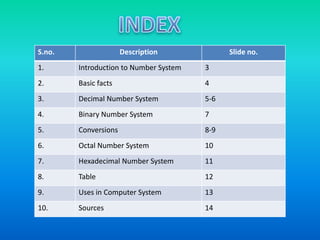
- 2. S.no. Description šÝšÝßĢ no. 1. Introduction to Number System 3 2. Basic facts 4 3. Decimal Number System 5-6 4. Binary Number System 7 5. Conversions 8-9 6. Octal Number System 10 7. Hexadecimal Number System 11 8. Table 12 9. Uses in Computer System 13 10. Sources 14
- 3. ïA number system defines how a number can be represented using distinct symbols. A number can be represented differently in different systems. ïMany number systems were introduced with the passage of time, like: âĒDecimal number system âĒBinary number system âĒOctal number system âĒHexadecimal number system
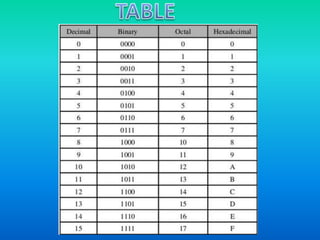
- 4. âĒA unit of information expressed as either a 0 or 1 in binary notation. âĒA group of binary digits or bits (usually eight) operated on as a unit. âĒA byte is considered as a unit of memory size. âĒThe base is the number of digits used in it. âĒThe larger the base, the more numerals are required. Decimal- Base 10 Binary- Base 2 Octal- Base 8 Hexadecimal- Base 16
- 5. The need for counting has paved the path to introduce decimal number system in which 10 digits 0,1,2,3âĶ9 are used to form any number. Most of our arithmetic operations are performed with decimal numbers. âĒThe prefix âdeciâ stands for 10. âĒThe decimal number system is a base 10 number system. âĒEach number can be used individually or they can be grouped to form a numeric value. âĒExample- 52, 16.83, -243 etc. ïThe value of each digit in a number depends upon the following: ï§The face value of the digits ï§The base of the number system ï§The position of the digit in the number
- 8. Conversion of decimal number into binary system. The rules are: 1. Divide the given decimal number with the base 2. 2. Write down their remainder and divide the quotient again by 2. 3. Repeat the step 2 till the quotient is 0. Example-
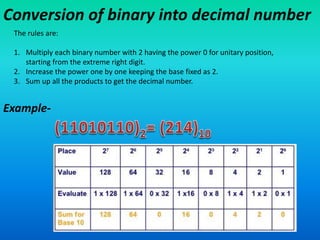
- 9. Conversion of binary into decimal number The rules are: 1. Multiply each binary number with 2 having the power 0 for unitary position, starting from the extreme right digit. 2. Increase the power one by one keeping the base fixed as 2. 3. Sum up all the products to get the decimal number. Example-
- 10. âĒOctal (base 8) was previously a popular choice for representing digital circuit numbers in a form that is more compact than binary. âĒThe octal number system consists of 8 digits i.e. 0 to 7 with the base 8. âĒ1 octal digit is equivalent to 3 bits. Examples: 278 = 2Ã81+7Ã80 = 16+7 = 23 308 = 3Ã81+0Ã80 = 24 43078 = 4Ã83+3Ã82+0Ã81+7Ã80= 2247
- 11. âĒThe prefix âhexaâ stands for 6 and the prefix âdeciâ stands for 10. âĒThis number system contains 16 systems and therefore has the base 16. âĒIt uses the digits (0-9) and (A-F). âĒNumbers are 0, 1, 2âĶ8, 9, A, B, C, D, E, F. B is 11, E is 14. âĒ1 Hex digit is equal to 4 bits. âĒEach place value in a hexadecimal number is a power of 16. Examples: 2816 = 28H = 2Ã161+8Ã160 = 40 2F16 = 2FH = 2Ã161+15Ã160 = 47 BC1216 = BC12H = 11Ã163+12Ã162+1Ã161+2Ã160= 48146
- 13. 1. A switch is just used to turn ON or turn OFF any desired deviceâĶ using the concept binary system. 2. Electronic Circuitry uses the octal system and hexadecimal system. 3. Decimal number system uses basic calculation and complex calculation in daily life.
- 14. âĒwww.easytechtips24.com/ âĒwww.aqua-calc.com/ âĒwww.rapidtables.com/ âĒI.T. Apps School Book Class 7 âĒwww.wikipedia.org/