PRML 2.4
- 1. PRML 2.4 指数型分布族 5501 酒井?徳 10/11/17
- 2. 目次 2.4 指数型分布族 ? 2.4.1 最尤推定と?分統計量 ? 2.4.2 共役事前分布 ? 2.4.3 無情報事前分布
- 3. <latexit sha1_base64="BWB9IVpNwEL+vV2Y0EHq4a+x7jI=">AAADX3ichVG7btRAFL1eAwkBEgMNiGaU1aKkWY0jJBASUiQkRAWbxyaR4rCyveO1Fb9kj5csZn+AH6CgAokC8Qe0FPADFCkpUcog0VBwPGuJxwYYyzNnzr3nPuY6aRjkkvNDraGfOn1mZvbs3LnzF+YXjIuXtvKkyFzRdZMwyXYcOxdhEIuuDGQodtJM2JETim1n/25l3x6KLA+SeFOOUrEX2YM48ALXlqB6xruULTErsqXveKxkB2zMnjLLScJ+PopwgLOEtEEvszvMn3JeZoOKO1lgiYOUWaHwpFWe7POoglXALALaBDP+JUGB23RCKwsGvrTGPaPJ21wtNg3MGjSpXp3E+EAW9SkhlwqKSFBMEjgkm3J8u2QSpxTcHpXgMqBA2QWNaQ7aAl4CHjbYfewD3HZrNsa9ipkrtYssIf4MSkYt/om/4cf8I3/Lv/Dvf41VqhhVLSOczkQr0t7Csysb3/6rinBK8n+qoGj9o2pJHt1S1QaoPlVM1Yc7iTB88vx44/Z6q7zOX/EjdPCSH/L36CEefnVfr4n1F6qiTGkEPVY9R6qKGK9cwpYjQx82D1yB95CIXCKTT8PqRTFA889xTYOtlbbJ2+bajebqg3qUs3SNFmkJ87pJq3SfOtQlV2PaPe2h1ml81mf0ed2YuDa0WnOZflv61R+AB9N4</latexit> 指数型分布族-定義 ?上の指数型分布族 ? ?はスカラーでもベクトルでも、離散でも連続でもよい ? : ?然パラメータ ? : 任意の関数 ? : 正規化係数 <latexit sha1_base64="oNLaS18gT0oNMOLaTbSICXWlyhA=">AAACtnichVHNahNRFP46VltrtaluBDfFkOIqnBGhpauAG1fSH9MWmjbMTG7SofPHzE1COvQFfAEX4kJBRXwMF+0LdNFHKF1WcOPCb24Gihb1DnPPud853/l1k8DPtMjZhHVj8uatqenbM3dm796bq8zf38zifuqpphcHcbrtOpkK/Eg1ta8DtZ2kygndQG25B88L+9ZApZkfR6/0KFG7odOL/K7vOZpQuzLfcuOgk41CiryltHPUrlSlLuYsXFfsUqmiPKtx5RgtdBDDQx8hFCJo6gEcZPx2YEOQENtFTiyl5hu7whFmyO3TS9HDIXrAu8fXTolGfBcxM8P2mCXgn5K5gJqcyhe5lBP5Kufy86+xchOjqGVE6Y65KmnPvX648eO/rJBSY/+KRUbtH1VrdLFsqvVZfWKQog9vHGFw+OZyY2W9li/KB7lgB+/lTL6xh2jw3fu4ptbfmopSw1EYmp5DU0XEKee0ZczQoa1LrM95aEbOmWkfg2KiXKD957quK5tP67bU7bVn1cbLcpXTeITHeMJ9LaGBF1hFk9mHeIdP+GwtW3uWsnpjV2ui5DzAb8dKfgHHO57C</latexit> <latexit sha1_base64="6fTy1Kd3WBF8Knfai0GtAN8nS1Q=">AAACwHichVHLThRBFD00KogPBtyYsKk4GYObSTUxgbAisHFleA2QMGTS3VMz06FfdtcMGTos2PIDLlxpYoxxo9/gAn/ABZ9gXGLixoWnazoxStTqdN1b595zn24S+JmW8mLMGr92/cbE5M2pW7fv3J2uzMzuZHE/9VTDi4M43XOdTAV+pBra14HaS1LlhG6gdt3DtcK+O1Bp5sfRth4m6iB0upHf8T1HE2pV5rpiXjTdOGhnw5BC5KKptCNOxCPRqlRlXZojrip2qVRRnvW4co4m2ojhoY8QChE09QAOMn77sCGREDtATiyl5hu7wgmmyO3TS9HDIXrIu8vXfolGfBcxM8P2mCXgn5IpUJOf5Vt5KT/Jd/KL/PHXWLmJUdQypHRHXJW0ps/ub33/Lyuk1Oj9YpFR+0fVGh0smWp9Vp8YpOjDG0UYHD+/3FrerOUP5Sv5lR28lBfyI3uIBt+81xtq84WpKDUchSPTc2iqiDjlnLaMGdq0dYj1OQ/NyDkz9TAoJsoF2n+u66qys1C3Zd3eeFxdeVquchJzeIB57msRK3iCdTSY/RRv8B4frFWrZ8XWs5GrNVZy7uG3Yx3/BBXsoL4=</latexit> <latexit sha1_base64="Lp9CNBX501YmHmYIv6M8R3pOEzM=">AAACxHichVFNa9RQFD2NVtta7VQ3BRcGh5G6GW5EsLgqCOJK+jVtoS1Dkr7phOaL5GW0hrpz4x9w4Uqhi9Kt/gIX+ge66E8QlxXcuPDkTaBoUV/Ie/eee8/99NIwyLXIyYh14eLopctj4xNXJq9em2pMX1/NkyLzVcdPwiRb99xchUGsOjrQoVpPM+VGXqjWvN1HlX1toLI8SOIVvZeqrcjdiYNe4LuaULdxazNydd/r2aVd2Pv2rH2mP6d+t9toSlvMsc8LTi00UZ+FpPEZm9hGAh8FIijE0JRDuMj5bcCBICW2hZJYRikwdoV9TJBb0EvRwyW6y3uH2kaNxtSrmLlh+8wS8s/ItNGSYzmUU/kiR/JVfv41VmliVLXs8fWGXJV2p17PLP/4Lyviq9E/Y5HR+kfVGj3MmWoDVp8apOrDH0YYvHhzuvxwqVXekffyjR28kxP5xB7iwXf/YFEtvTUVZYaj8Mz0HJkqYk65pC1nhm3aesQKzkMzcslMfQyqiXKBzp/rOi+s3ms70nYW7zfnn9arHMNN3MYs9/UA83iCBXSY/RWO8AEfrcdWaOVWMXS1RmrODfx2rJe/AIPQohc=</latexit> <latexit sha1_base64="rwWNb9jez2dQJlyUCzipX+NVqjo=">AAADV3ichVHLbtNAFL1OoITyaAqbSmxGREFlE40RElUlUCUWdIX6SlupLpHtjONR/ZI9Dg1WfoAfYMEKJBaIHb/AAn6ART4BsSwSGyQ4nliipQUmiufOOfecuXeukwQyU5xPjFr93PmZC42Ls5cuX7k615y/tp3FeeqKrhsHcbrr2JkIZCS6SqpA7CapsEMnEDvOwcOS3xmKNJNxtKVGidgP7UEkPenaClCv+X7AFpnlxEE/G4XYWMEsoWw2ZreZJSPF/JIPbeU7HrjDKSEOE2YFwlNWcbb4SRmWqjREtAVkfMwlx+kM11QOfGWNjwn7J2Rl2n1m9pot3uF6sdOBWQUtqtZa3PxIFvUpJpdyCklQRApxQDZl+O2RSZwSYPtUAEsRSc0LGtMstDmyBDJsoAf4DnDaq9AI59Iz02oXtwT4p1AyavPP/C0/4p/4O/6F//irV6E9ylpG2J2pViS9uecLm9//qwqxK/J/q6Bo/6NqRR4t6Wolqk80UvbhTh2Gz14cbS5vtItb/DX/ig5e8Qn/gB6i4Tf3zbrYeKkrSrVG0FPdc6iriPDKBbgMN/TBecByvIeCc4GbfBqWL4oBmn+O63Swfadj8o65fre18rgaZYNu0E1axLzu0Qqt0hp1yTUWjAfGI2O1Nqn9rM/UG9PUmlFprtOJVZ//BUME0aI=</latexit>
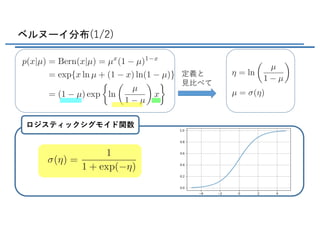
- 4. <latexit sha1_base64="WxpEywJNxWBX/SkIognSlOk6l8s=">AAADj3ichVFNb9NAEB3XfJTw0RQuSFxWRKlSIaJ1hVSEVBTBBS4obUlbqVsi210nVu21tV6bFBPBmT/AgRNIHBA/gwP8AQ79CcCxSFw4MLsxglABG8U7++a9N7M7XhqFmaL0wJqxjx0/cXL2VO30mbPn5urz5zeyJJc+7/lJlMgtz814FAreU6GK+FYquRt7Ed/09m7r/GbBZRYm4r7aT/lO7A5EGIS+qxDq1z+npEVG5DFhcU4WycIKYUnKpasSKdyYk5Lc4lKQ8RRrxewPMDkyGYdcrTIa0yeNM1bTdnyUEqaZLBKGdaVSjJCvsd/17KdsCjQWEQ8U+hgXHbcIC6TrY0HNGleFJzGT4WCoFnVRExnbfr1B29QscjRwqqAB1eom9ffAYBcS8CGHGDgIUBhH4EKGv21wgEKK2A6UiEmMQpPnMIYaanNkcWS4iO7hd4Cn7QoVeNaemVH7WCXCv0QlgSb9SN/QQ/qBvqWf6Pe/epXGQ/eyj7s30fK0P/fs4vq3/6pi3BUMf6lQ0fxH1woCuG66DbH71CD6Hv7EoXj0/HD9xlqzXKCv6Be8wUt6QN/hHUTx1X+9ytdemI6k0XB4aO4cmy4EvnKJuQwr7GIuQCzH91DoXGKlIRT6RXGAzp/jOhpsLLUd2nZWrzU696pRzsIluAwtnNcydOAOdKEHvtW1CuuJ9dSet5ftm3ZnQp2xKs0FmFr23R8R3tpM</latexit> ベルヌーイ分布(1/2) 定義と ??べて ロジスティックシグモイド関数 <latexit sha1_base64="f05bLch8sZ6JPXca9kf7owNZ0yw=">AAAC2HichVFLaxRBEK6Mrxgf2ehF8NK4rMSDS00UDIIQ8OJJ8nCTYCYsM5Oe3SbzoqdnJQ4Bb6JHLyKeFDyIP8KDB+MP8JCfIB4jePHgN70DokGtoaerv6qvnkEeq8Iw7084R44eO35i8uTUqdNnzk63Zs6tFlmpQ9kLszjT64FfyFilsmeUieV6rqWfBLFcC7Zv1/a1kdSFytJ7ZieXm4k/SFWkQt8A6reuedL44pbw4hRHRmZWeJH2Q1EJLynFLm5XXG10T6vB0Fzpt9rcZSvisOI2SpsaWcxaH8mjLcoopJISkpSSgR6TTwW+DXKJKQe2SRUwDU1Zu6RdmgK3hJeEhw90G/8BXhsNmuJdxywsO0SWGEeDKajDn/ktH/Aev+Mv/OOvsSobo65lB3cw5sq8P/30wsr3/7IS3IaGv1hgdP5RtaGI5m21CtXnFqn7CMcRRg+fH6zcXO5Ul/k1f0UHr3ifP6CHdPQtfLMkl1/airTlSHpge05sFSmmXMFWIMMWbBGwEvMwiFwh05BG9USxQPfPdR1WVue6LnfdpevthbvNKifpIl2iWezrBi3QHVqkHrK/oPe0R5+c+84j57HzZOzqTDSc8/SbOM9+ArOSqTI=</latexit> <latexit sha1_base64="XZsERPW3Ppgw3cMHk0c02FLPHNo=">AAACunichVHLahRBFD1pXzE+MiqC4KZxGImb4bYIiigE3LiSPJwkkAlDd6dmUky/6K4eiY0/4A+4cBXBheYzXJgfyCKfIC4juHHh6ZoG0aDepqtunXvPfQZZpAsjcjTjnDp95uy52fNzFy5eujzfunJ1rUjLPFS9MI3SfCPwCxXpRPWMNpHayHLlx0Gk1oPxk9q+PlF5odPkudnN1FbsjxI91KFvCA1a1/tx6T52+4Uexb674PaV8d07g1ZbumLFPal4jdJGI0tp6zP62EaKECViKCQw1CP4KPhtwoMgI7aFilhOTVu7wivMkVvSS9HDJzrmOeJrs0ETvuuYhWWHzBLxz8l00ZFD+SDHciD78kV+/DVWZWPUtezyDqZclQ3mX99Y/f5fVszbYOcXi4zOP6o2GOKBrVaz+swidR/hNMLk5Zvj1Ycrneq2vJOv7GBPjuQTe0gm38L3y2rlra0otxyFF7bn2FaRcMoVbQUzbNM2JFZyHoaRK2bawaSeKBfo/bmuk8ra3a4nXW/5XnvxWbPKWdzELSxwX/exiKdYQo/ZK+zhI/adR07gaGc8dXVmGs41/CaO+QnZsp44</latexit> <latexit sha1_base64="3Wyg+fYmH5I++xlEcrRVfW7WThw=">AAAC2nichVE7axRRFP4yvmJ8ZNVGsLm4rETE5U5QFEEI2FhJHm4SyITlzuTuZsi8mLm7Godt7NRWsEilYCH+CrFQtLbITxDLCDYWfnN3RDSoZ5h7z/3O+c7Tz6KwMFLuTjgHDh46fGTy6NSx4ydOTjdOnV4u0kEe6E6QRmm+6qtCR2GiOyY0kV7Ncq1iP9Ir/tatyr4y1HkRpslds53p9Vj1k7AXBsoQ6jauekXYj5WYEZ42SlwUN4XXy1UgSuGKkT0v0XQ/o8flnz6jbqMp29KK2K+4tdJELfNp4x08bCBFgAFiaCQw1CMoFPzW4EIiI7aOklhOLbR2jRGmyB3QS9NDEd3i2edrrUYTvquYhWUHzBLxz8kUaMlP8pXck+/la/lZfv9rrNLGqGrZ5u2PuTrrTj8+u/Ttv6yYt8HmLxYZrX9UbdDDdVttyOozi1R9BOMIwwfP9pZuLLbKC/KF/MIOnstd+ZY9JMOvwcsFvbhjK8otR+Oe7Tm2VSSccklbwQwbtPWIDTgPw8glM21iWE2UC3T/XNd+ZXm27cq2u3ClOXenXuUkzuE8Zriva5jDbcyjw+w7eIMP+Oh4zkPnkfNk7OpM1Jwz+E2cpz8A8QGn7A==</latexit>
- 5. ベルヌーイ分布(2/2) ベルヌーイ分布 ただし、 ? ベルヌーイ分布は指数型分布族である <latexit sha1_base64="cNBKBkDQN667KdSE9y8Kzu0z98E=">AAAC13ichVHLahRBFD1po8b4yKgbwU3hMJIsHKpDQBGEgBtXkoeTRDJh6O7UTIr0i+6acWIr7kTcuVJwpeAi+A9uXCQ/4CKfIC4juHHh6ZoW0aBW01X3nnvPffppqHMj5cGYc2z8+ImTE6cmT585e26qdv7CSp70s0C1giRMsjXfy1WoY9Uy2oRqLc2UF/mhWvW3b5f21YHKcp3E98xOqjYirxfrrg48Q6hTm03FtBiKR6KtjCdmxC3RznUv8ohe+4m11bD0stpQzHRqddmU9oijglsJdVRnIantoY1NJAjQRwSFGIZyCA85v3W4kEiJbaAgllHS1q7wGJPk9uml6OER3ebdo7ZeoTH1MmZu2QGzhPwzMgUa8pPclYdyX76Xn+X3v8YqbIyylh2+/oir0s7U80vL3/7LivgabP1ikdH4R9UGXdyw1WpWn1qk7CMYRRg8fHm4fHOpUVyVb+UXdvBGHsiP7CEefA3eLaql17aizHIUHtieI1tFzCkXtOXMsElbl1if8zCMXDDTFgblRLlA9891HRVWZpuubLqLc/X5u9UqJ3AZVzDNfV3HPO5gAS1mf4UP2MO+c9954jx1no1cnbGKcxG/HefFD2lJpvw=</latexit> <latexit sha1_base64="PTFxSGCE4LUfjwH0GeRl5vsWABE=">AAADHHichVHLahRBFL3d8RFjYkbdCG4Kh5G4cKgOgiIIATeuJA8nCaTD0N1T01OkX1RXTxyb+QF/wIUgKLgQP0NBQVwqZOEHiMsIblx4uqZH0aBW07dunXvPffpZJHPN+YFlzxw7fuLk7Km50/MLZxYbZ89t5mmhAtEJ0ihV276Xi0gmoqOljsR2poQX+5HY8vduV/atoVC5TJN7epSJ3dgLE9mXgacBdRv7biT6us1cX4QyKT2lvNGYlSxilSzYErvPrrBbkGPmuoAGPyFnCoWAXKE9g7q5DGMPyNUpBi+R9KahXSXDgW53G03e5uawo4pTK02qz2raeEMu9SilgAqKSVBCGnpEHuX4dsghThmwXSqBKWjS2AWNaQ7cAl4CHh7QPcgQr50aTfCuYuaGHSBLhF+ByajFP/AX/JC/5S/5Z/79r7FKE6OqZYTbn3BF1l18eGHj239ZMW5Ng18sMFr/qFpTn26YaiWqzwxS9RFMIgwfPDrcuLneKi/zZ/wLOnjKD/gr9JAMvwbP18T6Y1ORMhxB+6bn2FSRYMolbDky9GDrAyswD43IJTINaFhNFAt0/lzXUWVzue3wtrN2rblyt17lLF2kS7SEfV2nFbpDq9RB9k/WjDVvLdhP7Nf2O/v9xNW2as55+u3YH38AK4e8eQ==</latexit>
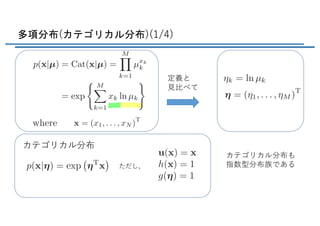
- 6. 多項分布(カテゴリカル分布)(1/4) 定義と ??べて カテゴリカル分布 ただし、 カテゴリカル分布も 指数型分布族である <latexit sha1_base64="pgsB2JMEvghlBqmK6lDL7Rl8OYY=">AAADiHicjVG7bhNREJ3N8gjmEQMNEs0VliOnse5GSAEkpIg0UIDywEmk3GDtru/aK+9Lu3eNzeIf4AcoqECiQHwGBfwARepUEWWQaCg4+xBRCK9reWfumTlnZu5YkecmivM9bUY/dfrM2dlztfMXLl6aq1++spmEaWzLjh16YbxtmYn03EB2lKs8uR3F0vQtT25Zw5U8vjWSceKGwWM1ieSub/YD13FtUwHq1vcj1mLCN9XAcljGxmzKnjNhhV4vmfgwwISfAl1g83eZUHKsshVTTVv/wVlgYERx2GNdQEPcDKQ+gf8QNk8p8RIb/7whJmp5NTmOmPCkowQUk9T/rc4RT3jBMVURu/2BEtNuvcHbvDjspGNUToOqsxrWP5KgHoVkU0o+SQpIwffIpAS/HTKIUwRslzJgMTy3iEuaUg3cFFkSGSbQIb593HYqNMA910wKto0qHv4xmIya/DN/xw/5J/6eH/Dvf9TKCo28lwmsVXJl1J17cW3j2z9ZPqyiwRELjOZfulbk0K2iWxfdRwWSz2GXCqNnLw837qw3s3n+hn/BBK/5Hv+AGYLRV/vtmlx/VXQUFxxJT4uZ/aKLAK+cIZagQg8xB1iK91BQzlBpQKP8RbFA49d1nXQ2F9sGbxtrNxvLj6pVztJ1ukEt7GuJluk+rVKHbO2BFmpjbaLXdK4v6bfL1Bmt4lylY0e/9wOZy94u</latexit> <latexit sha1_base64="RDIjsG/lgO0jV2r/H+AwqRFREpg=">AAAC9nichVHLahRBFD1pXzE+MtGN4KZxGIkgQ7UIBkEIuHEVMkkmCWTi0N1TPdOkX1TXjInN/IA/4EIQFIKIG3d+gAv9ARdZuFXEZQQ3Ljxd0yAa1Gq66txz69xHXS+LwlwLcTBlHTt+4uSp6dMzZ86eOz9bm7uwnqdD5cu2n0ap2vTcXEZhIts61JHczJR0Yy+SG97O3dK/MZIqD9NkTe9lcjt2+0kYhL6rSXVrrU7s6oEX2IW9a4/tO3YnkoGep9El5ZC6TqqX6pxgQi6R7KiwP9DX7Pu0TQQVE63RM+7W6qIpzLKPAqcCdVRrOa29Qwc9pPAxRAyJBJo4gouc3xYcCGTktlGQU0Sh8UuMMUPtkLckb7hkd7j3aW1VbEK7jJkbtc8sEX9FpY2G+CBeikPxXrwSX8SPv8YqTIyylj2e3kQrs+7so0ur3/+rinlqDH6pqGj8o2qNAAum2pDVZ4Yp+/AnEUYPHx+u3l5pFFfFc/GVHTwTB+Ite0hG3/z9llx5YipSRiPxwPQcmyoSvnJBX84MPfoCckO+h2bkgpkGGJUvygE6f47rKFi/0XRE02ndrC8uVaOcxmVcwTzndQuLuIdltJn9DT7iEz5bu9ZTa996MblqTVWai/htWa9/AlA4syw=</latexit> <latexit sha1_base64="pYtNZg2paon8StH4xBwbnoJgSFY=">AAACr3ichVHLThRRED00KAOoDLoxcUOcjGE1qSYkEFYkblwRXsOQMIDdTQ1zQ7/SfWdg7PADfoAuXCgmLoif4UJ+wAWfYFxCwoYF1Xc6MULA6vS9dU/Vqacb+yrVRGcD1uDQg4fDpZHRsUePn4yXJ56up1En8bjuRX6UbLhOyr4Kua6V9nkjTtgJXJ8b7v7r3N7ocpKqKFzTvZi3AmcvVC3lOVqgZlPzoc4O2pzw0U65QjUyMnlbsQulgkKWovJPNLGLCB46CMAIoUX34SCVbxM2CLFgW8gES0RTxs44wqhwO+LF4uEIui/nnrw2CzSUdx4zNWxPsvjyJ8KcRJV+0Qmd0yl9p990dWeszMTIa+nJ7fa5HO+Mv3++evlfViC3RvsvSxjVe6rWaGHOVKuk+tggeR9eP0L33cfz1fmVavaKvtIf6eCYzuiH9BB2L7xvy7zyyVSUGA7jwPQcmCpCmXImtlQy7IqtJVhH5qElciaZ2ujmE5UF2jfXdVtZn67ZVLOXZyoLi8UqS3iBl5iSfc1iAW+whLpkj/EBn/HFsq2GtW297btaAwXnGf4RS10DCm2ccg==</latexit> <latexit sha1_base64="0gnbcP56TCCsKG97xdT4fWwx6eQ=">AAADA3ichVE9axRBGH6z8SPGj5ymEWwWj5MIcsyKoAhCIE0aJV+XBLLJsbs3dzdk9oOZuZPLcmWa/IEUVgoWkk5srRT0D1jkJ6jlBWwsfHZuRTSos+zMM887z/sZZlJow9jxhDN55uy581MXpi9eunxlpnL12rpOeyrijSiVqdoMA82lSHjDCCP5ZqZ4EIeSb4S7C4V9o8+VFmmyZgYZ346DTiLaIgoMqGZlxw9T2dKDGIebuz43gTt0H7m+5G0zN743YfDA3gHbSo0uwE/+MXhfiU7X3HZ3CgdxYLoqBlqDZdisVFmd2eWeBl4JqlSupbTygXxqUUoR9SgmTgkZYEkBaXxb5BGjDNw25eAUkLB2TkOahraHVxwvArC72Du4bZVsgnvhU1t1hCgSv4LSpRr7xF6xEfvIjthn9v2vvnLro8hlgDMca3nWnDm4vvrtv6oYp6HuLxUUtX9kbahND2y2AtlnlinqiMYe+nuHo9WHK7X8FnvBvqKC5+yYvUMNSf8kernMV57ZjJTVcHpqa45tFgm6nMOmEaEFWxtcD/0w8JwjUpf6RUcxQO/PcZ0G63frHqt7y/eq80/KUU7RDbpJc5jXfZqnRVqiBqK/py80ohNn3zlyXjtvxk+diVIzS78t5+0PeJy4zA==</latexit> <latexit sha1_base64="DKjDjznH1ZCW7iILelJ4hAKZtVg=">AAACw3ichVHLahRBFD1pXzE+MupGEKRwGHE13A6CIggBEVxJHk4SyIShu1OTNNMvuqtHYjM7V/6AC1cKLtSl/oEL/QEX+QRxGcGNC0/XtIgG9TZddevce+7Tz6KwMCL7M86Ro8eOn5g9OXfq9Jmz861z59eKtMwD3QvSKM03fK/QUZjonglNpDeyXHuxH+l1f3Sntq+PdV6EafLA7GV6K/Z2knAYBp4hNGhd7mvjqYGq1EhN1G3VjxLVj8ufyKDVlq5YUYcVt1HaaGQpbX1AH9tIEaBEDI0EhnoEDwW/TbgQZMS2UBHLqYXWrjHBHLklvTQ9PKIjnjt8bTZowncds7DsgFki/jmZCh35JK/kQD7KG/ks3/8aq7Ix6lr2ePtTrs4G808urn77LyvmbbD7i0VG5x9VGwxx01YbsvrMInUfwTTC+NHTg9VbK53qqryQL+zguezLe/aQjL8GL5f1yjNbUW45Gg9tz7GtIuGUK9oKZtimbUis5DwMI1fMtItxPVEu0P1zXYeVtYWuK113+Xp78X6zyllcwhVc475uYBH3sIQesz/Ga7zFO+euM3Jyx0xdnZmGcwG/iTP5AZkCoU4=</latexit> <latexit sha1_base64="Yku9sR18JNFtp86XEzFbAx+JetQ=">AAADHHichVHLahRBFL3d8RFjYkbdCG4Kh5HJZqgWwRAQAm5cSV6TBNJx6O6pninSL6prJhnb+QF/wIUgKLgQP0NBQVwqZOEHiMsIblx4uqZBTHxU01Wnzr3nPur6WSRzzfmhZU+dOn3m7PS5mfOzcxfmaxcvbebpQAWiHaRRqrZ9LxeRTERbSx2J7UwJL/YjseXv3SntW0OhcpkmG3qUid3Y6yUylIGnQXVq+xlrMjf2dN8PWcEO2Jg9ZK6fRt18FOMA5wrtgV5gtwEPMuZGItTNPzvdL2EZTcVAG2DGx6K7Svb6eqFTq/MWN4udBE4F6lStlbT2llzqUkoBDSgmQQlp4Ig8yvHtkEOcMnC7VIBTQNLYBY1pBtoBvAQ8PLB72Hu47VRsgnsZMzfqAFki/ApKRg3+kb/kR/wdf8W/8B9/jVWYGGUtI5z+RCuyzvyjK+vf/6uKcWrq/1JB0fhH1ZpCWjTVSlSfGabsI5hEGD54fLS+tNYorvPn/Cs6eMYP+Wv0kAy/BS9WxdoTU5EyGkH7pufYVJHglQvYcmTowhaCG+A9NCIXyNSnYfmiGKBzfFwnweaNlsNbzurN+vK9apTTdJWuURPzukXLdJdWqI3sn60pa9aas5/ab+z39oeJq21Vmsv027I//QRkDsCa</latexit> <latexit sha1_base64="Zniw459cl9C+fyel5Lnw6RcdJdI=">AAADTHichVFPa9RAFH9JtdZq7VovgpfgslIvYaKCIi0UvHiS/nHbQlOWSXaSDJ1MwmSy7Rr2C/gFPHhSEBE/hgc9efPQjyAeW/Cggi+zKdbWPxMy897vvd/7G+SCF5qQfcueOHN28tzU+ekLF2cuzbYuz60XWalC1g0zkanNgBZMcMm6mmvBNnPFaBoIthHsPKjtGwOmCp7Jx3qYs+2UxpJHPKQaoV7rtS9YpF3HD1jMZUWVosORUznCqW8/pToJIpRK1OeP6Xuo33QWTyAjx/dRTP7o6h2Z49ocZKJfDFN86jxM0+NeTPaPSvEVjxPt9lpt4hJznNOC1whtaM5y1noPPvQhgxBKSIGBBI2yAAoFflvgAYEcsW2oEFMocWNnMIJp5JboxdCDIrqDd4zaVoNK1OuYhWGHmEXgr5DpQId8Im/IAflA3pLP5PtfY1UmRl3LEN9gzGV5b/bp1bWv/2Wl+GpIfrGQ0flH1RoiuGeq5Vh9bpC6j3AcYfDk2cHa/dVOdYO8JF+wgxdkn7zDHuTgMHy1wlafm4qU4TDYNT2npgqJU67QVmCGPtoixEqch8bIFWZKYFBPFBfonVzXaWH9lusR11u501561KxyCq7BdZjHfd2FJXgIy9CF0JqxblsL1qL90T60v9k/xq621XCuwG9nYvInbCrODg==</latexit>
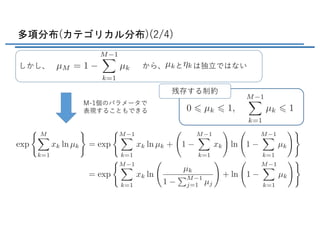
- 7. 多項分布(カテゴリカル分布)(2/4) しかし、 から、 と は独?ではない M-1個のパラメータで 表現することもできる 残存する制約 <latexit sha1_base64="plqF8fnBWnxdNaHitAh5XqPw/HA=">AAADBXichVHLahRBFD1pXzE+MupGcFM4jLjQ4bYIiiAE3LhR8nCSQDqO3T01STPVj3RVj8Rm1oI/4MKVggsRd+LWhaD+gIt8guguPjYuvF3T4CNEq+mqU+fecx91g0xF2hBtTTh79u7bf2Dy4NShw0eOTjeOHV/UaZGHshOmKs2XA19LFSWyYyKj5HKWSz8OlFwKBtcq+9JQ5jpKk1tmM5Orsb+WRP0o9A1T3cYdEp6SG1r5iRFeXIiuKMVAjH5jXXFOeBuF3xOeLuLa4SrTI3Gb8Q1x3uJdxN1Gk9pkl9gJ3Bo0Ua/ZtPEOHnpIEaJADIkEhrGCD83fClwQMuZWUTKXM4qsXWKEKdYW7CXZw2d2wPsa31ZqNuF7FVNbdchZFP85KwVa9IGe0Ta9p+f0kX7sGqu0MapaNvkMxlqZdacfnFz4/l9VzKfB+i8VK1r/qNqgj8u22oirzyxT9RGOIwzvPdxeuDLfKs/QE/rEHTymLXrDPSTDL+HTOTn/yFaUW43EXdtzbKtI+JVLtmnO0GNbn7mC38Nw5JIzrWNYvSgP0P17XDvB4oW2S2137mJz5mY9ykmcwmmc5XldwgyuYxYdzv4Wn/EV35z7zgvnpfNq7OpM1JoT+GM5r38Cqoy4Xg==</latexit> <latexit sha1_base64="7V2dfGCalLluvsI0OBuVlTdTA2Q=">AAACx3ichVFLS9xQFP6Mtlpr69RuCt0Eh5FuHE5KQREEwY1dWHyNCo4NSbyjYfIiuUnVMIvuSv9AF10pdCGC23bfRf0DLvwJ0qWCmy56cidQWqmekHvP/c75ztOOPDeRROc9Wm/fvfv9Aw8GHw49ejxceTKymoRp7IiGE3phvG5bifDcQDSkKz2xHsXC8m1PrNnt2cK+lok4ccNgRe5FYtO3tgO35TqWZMisjDb91JzXp3VjXG8mqW/m7Wmj8zafHzc6eWFrd8xKleqkRL+pGKVSRSkLYeUHmthCCAcpfAgEkKx7sJDwtwEDhIixTeSMxay5yi7QwSBzU/YS7GEx2uZzm18bJRrwu4iZKLbDWTz+Y2bqqNEZHdElndIxXdCv/8bKVYyilj2+7S5XRObwx2fL13eyfL4ldv6wmFG7pWqJFiZVtS5XHymk6MPpRsj2P10uTy3V8jE6pJ/cwQGd03fuIciunC+LYumzqihWHIF3qmdfVRHwlHO2JZxhi20txlKeh+TIOWfaQVZMlBdo/Luum8rqy7pBdWPxVXXmTbnKATzHKF7wviYwgzksoMHZP+AEX/FNe62FWqbtdl21npLzFH+J9v43P6ykEg==</latexit> <latexit sha1_base64="IzW16R2yDJtpmhkKDinFPtB+M8s=">AAACqHichVHLahRBFD1pXzE+MupGyCY4jIiL4XYQFFcBN65k8phMJAlDd6cmKaZfdFePxMYfcOPSBFcGshA/I4v4Ay7yCeIygpsscrqmQTSot+mqW+fec59+GurciBxPOBcuXrp8ZfLq1LXrN25ON27dXsmTIgtUN0jCJFv1vVyFOlZdo02oVtNMeZEfqp4/fFbZeyOV5TqJl81OqjYibyvWAx14hlB3PSr6w36jKW2xMntecWuliVo6SeMI69hEggAFIijEMNRDeMj5rcGFICW2gZJYRk1bu8IbTJFb0EvRwyM65LnF11qNxnxXMXPLDpgl5J+ROYuWfJVPciJf5LN8k9O/xiptjKqWHd7+mKvS/vTbu0s//8uKeBts/2KR0fpH1QYDPLHValafWqTqIxhHGL1+f7L0dLFV3pd9+c4OPsqxHLKHePQjOFhQix9sRZnlKLyyPUe2iphTLmnLmWGTtgGxgvMwjFwy0zZG1US5QPfPdZ1XVubarrTdhUfN+Rf1Kicxg3t4wH09xjyeo4Mus2u8wy72nIdOx+k5L8euzkTNuYPfxPHPAMbimQA=</latexit> <latexit sha1_base64="Z5Pl22ai4hoXSVuKkTo5uMmYTeo=">AAACqXichVFNT9RQFD0UFcQPRtmYuCFOxpCYTG4JCcQViRtWhgFnmAhk0pY3UKZfad8MgYY/wModUVeauDD8DBb6B1jwE4hLTNy48PRNE6NEuU3fu+/ce+6nmwR+pkXOR6zRGzdvjY3fnrhz9979ycqDh60s7qeeanpxEKdt18lU4EeqqX0dqHaSKid0A7Xm9l4U9rWBSjM/jl7p/URths525Hd9z9GEWhtKO51ep1KVuhiZvqrYpVJFKctx5Qs2sIUYHvoIoRBBUw/gIOO3DhuChNgmcmIpNd/YFQ4xQW6fXooeDtEez22+1ks04ruImRm2xywB/5TMadTkTD7LpXyVE7mQn/+MlZsYRS37vN0hVyWdyaNHqz+uZYW8NXZ+s8io/adqjS4WTLU+q08MUvThDSMMDo4vV5+v1PKn8lG+sYMPci6n7CEafPc+NdTKe1NRajgKe6bn0FQRcco5bRkzbNHWJdbnPDQj58y0g0ExUS7Q/ntdV5XWbN2Wut2Yqy6+LFc5jsd4ghnuax6LWMIymsy+izd4i3fWM6thta3XQ1drpORM4Q+xvF+0dpli</latexit> <latexit sha1_base64="fd3oy41FJPojCpAXUr96XJ/MSRQ=">AAAEmHicrVHLbtNAFL1xDZTwaNpuEGxGRKlaVY3GCKlVpUqRWAALUJuStqhTItsdJ278kj0OLZbFFvgBFqxAYoH4DBbwAyz6CYgdRWLDguuxoZSoJUJMFM+dM/ecOWfGCBw7EpTul5QR9dTpM6Nny+fOX7g4VhmfWIv8ODR5y/QdP9ww9Ig7tsdbwhYO3whCrruGw9eN3o1sf73Pw8j2vXtiL+Bbrt7xbMs2dYFQe7z0hfHdgDCHW4IlhEWxS9okIT2yRDSSkgdY38F5t0BTbPUIc+PDdWh3uoKl5amlYaTmZH283GwuMI1tc0NrSAszudaQ7MEIM7+iMEYwDfnnOLkFZoW6ifDvJ6U4H7G2c4K1HUn4aW72v8VrV6q0TuUgg4VWFFUoxrJfeQ8MtsEHE2JwgYMHAmsHdIjwtwkaUAgQ24IEsRArW+5zSKGM3Bi7OHboiPbw28HVZoF6uM40I8k28RQH/yEyCdToR/qGHtAP9C39RL8fq5VIjczLHs5GzuVBe+zZpdVvf2W5OAvoHrKQUTvBtQALFqRbG90HEslymLlC/9Hzg9XFZi2Zoq/oZ0zwku7Td5jB6381X6/w5gvpKJQcDg9lZle68PCWE9yL8IRt3LMQi/E+BConeFIX+tmN4gNqfz7XYLF2ra7RurZyvdq4WzzlKFyBqzCN7zUPDbgFy9ACU7mvPFaeKE/Vy2pDvanezluVUsGZhCNDbf4ALWMpWQ==</latexit>
- 8. 多項分布(カテゴリカル分布)(3/4) 元の式に 代?しなおすと、 全てのkについて ?し合わせる ソフトマックス関数 0 exp( ) ( ) exp( ) k k M ii x f x= = ? x (右辺) <latexit sha1_base64="THKcNOK4qWzxXlUiacxqMNDG3zE=">AAADE3ichVHLahRBFL3TiRrjIxPdCNkUDiMRYagWwSAIATeuQh5OEkiHobtTPVOZflFdPRqb/IB7cZFVAi4kn5BdFHTjThf5BHEZQRAXnq5pfMVHNV116tx77qOul4Yy05wf1ayR0VOnz4ydHT93/sLFifrkpeUsyZUv2n4SJmrVczMRyli0tdShWE2VcCMvFCte/15pXxkIlckkfqC3UrEeud1YBtJ3NahOPXainHVYwfpsm91lTqBcHzdHPEqZE4pATwNr97uLo2S3p68DFcxmN5iT5ZExbpbGP6k2f1Z16g3e4maxk8CuQIOqNZ/UX5NDG5SQTzlFJCgmDRySSxm+NbKJUwpunQpwCkgau6BtGoc2h5eAhwu2j72L21rFxriXMTOj9pElxK+gZNTk7/kLfszf8H3+gX/9a6zCxChr2cLpDbUi7Uw8ubL0+b+qCKem3g8VFM1/VK0poBlTrUT1qWHKPvxhhMHjZ8dLdxabxTW+xz+ig11+xF+ih3jwyX++IBZ3TEXKaAQ9ND1HpooYr1zAliHDBmwBuBzvoRG5QKYeDcoXxQDt38d1EizfbNm8ZS/caszOVaMcoym6StOY122apfs0T21kf0dfaiO1UeupdWAdWq+Grlat0lymX5b19huTYLv9</latexit> <latexit sha1_base64="hAaEbLVE27hLYBsb50lDVyDUK0U=">AAADSnichVHNbtNAEB67BUoKNMAFicuKKFF6SLRGSKCiSJW4cADUH9JW6hbLcdeJ41+t1yll5RfgBThwAqkHxGNwgANXDn0ExI0iIQQHxhsDggrYlb2z38z3zczOIA39TFJ6aJgzsydOnpo7XZs/c/bcQv38hY0syYXL+24SJmJr4GQ89GPel74M+VYquBMNQr45CG6V/s0JF5mfxPflfsp3ImcY+57vOhIhu37QYmFMWMg92SbME45LFGFRTmw8A1LgVsQiHcKyPNLgGKEfAWMdwIQ/HMlF0iOMS+cnk7Fai7A7qKz9jhDJ3jSFQr4dFMrqlKq2Gves4oG627EK7RkXRY/xh6lql3p2sFjY9QbtUr3IccOqjAZUayWpvwYGu5CACzlEwCEGiXYIDmS4t8ECCiliO6AQE2j52s+hgBpyc4ziGOEgGuB/iLftCo3xXmpmmu1ilhA/gUwCTfqOvqBH9A19Sd/Tb3/VUlqjrGUfz8GUy1N74fGl9c//ZUV4Shj9YiGj+Y+qJXhwQ1frY/WpRso+3KnC5NGTo/WltaZq0ef0A3bwjB7SV9hDPPnkHqzytae6IqE5HPZ0z5GuIsZXVujLMMMu+jzEcnwPicoKM41gUr4oDtD6c1zHjY2rXYt2rdVrjeV71Sjn4DJcgTbO6zosw21YgT64xrxhGUvGTfOt+dH8Yn6dhppGxbkIv62Z2e+h4M/d</latexit> <latexit sha1_base64="TSwki9nluWDHvkrir1/vyHRa8Js=">AAACyXichVE7axRRFP4yvmJ8ZBMbwSa4rthkuRMEJRAIpBFEycNNAtk4zEzuJpPMKzN31iSXqezyByysFCzExlZbC/0DFvkJYhnBxsJv7g6IBvUMc++53znfeXppGORKiKMh69TpM2fPDZ8fuXDx0uXRxtj4cp4UmS87fhIm2arn5jIMYtlRgQrlappJN/JCueLtzFX2lb7M8iCJH6n9VK5H7mYc9ALfVYScxo2Zbi9zfW2X2p7s5kXk6O0Zu3ysH0wS6kaFs12WTqMp2sLIxEnFrpUmaplPGh/RxQYS+CgQQSKGoh7CRc5vDTYEUmLr0MQyaoGxS5QYIbegl6SHS3SH5yZfazUa813FzA3bZ5aQf0bmBFris3gtjsUn8UZ8ET/+GkubGFUt+7y9AVemzujh1aXv/2VFvBW2frHIaP2jaoUe7ppqA1afGqTqwx9E6B88O16aXmzpm+Kl+MoOXogj8YE9xP1v/qsFufjcVJQZjsQT03Nkqog5ZU1bzgwbtPWIFZyHYmTNTFvoVxPlAu0/13VSWZ5q26JtL9xuzj6sVzmMa7iOW9zXHcziHubRYfZDvMU7vLfuW7vWnnUwcLWGas4V/CbW05/KsKXz</latexit> <latexit sha1_base64="qzp3qU05umwGmLLs2hbezjCXyog=">AAAC13ichVFLS9xQFP6M2qq1dbQboRtxGBFKhxMRKsKA4Kabio+OWhwbknhHw+RFcjOiYeiuFHeuLHRVwYX0P3TThf4BF/6E4lLBjYue3AmKlbYn5N5zv3O+87RC14kl0XmH1tnV/ehxT2/fk/6nzwYKg0PLcZBEtqjagRtEq5YZC9fxRVU60hWrYSRMz3LFitWYzewrTRHFTuC/kzuhWPfMTd+pO7YpGTIKE5VanHhG2qjorQ/p21ZaE9I0Gq2K/vKe4ZV+azIKRSqTkpGHip4rReQyHxROUMMGAthI4EHAh2TdhYmYvzXoIISMrSNlLGLNUXaBFvqYm7CXYA+T0Qafm/xay1Gf31nMWLFtzuLyHzFzBCU6o2O6pFP6Tr/o5q+xUhUjq2WHb6vNFaExsDe8dP1flse3xNYdixmlf1QtUceUqtbh6kOFZH3Y7QjN3YPLpenFUjpGh3TBHXyjc/rJPfjNK/toQSx+VRVFiiOwrXr2VBU+TzllW8wZNthWZyzheUiOnHKmLTSzifIC9T/X9VBZnijrVNYXJoszc/kqe/ACoxjnfb3GDN5gHlXO/gU/cIJT7b32UfukfW67ah055znuibb/G87Qq9c=</latexit> (左辺)
- 9. 多項分布(カテゴリカル分布)(4/4) カテゴリカル分布はソフトマックス関数を?いた表現においても によって対応付けられることから 指数型分布族の標準形になっている <latexit sha1_base64="cHNej5Ktg6qD7gUwtThF+p3Jjmo=">AAADd3ichVFLa9RQFD6Z+Kj10aluBBdeHKZMkQ43UrAIQsGNG6WvaQtNOySZm0mYvEhuxo5x/oB/wIUrBRfiz3Cha8FFf4K4rCCCC7/ciYpt1RuS8+U75zuPe+wk8DPJ+YFW00+dPnN26tz0+QsXL83UZy9vZnGeOqLjxEGcbttWJgI/Eh3py0BsJ6mwQjsQW/bgXunfGoo08+NoQ44SsRta/ch3fceSoLr1DwlrMTO0pGe7rGD7bMyeMNOOg142CmHAmUJaoOfZXWYGwpUtZrCbzMzykHXhHoA34N8DfsAWFDbFfvIzWMkngXCkft+T879sKTpBclL9MlQ1moZAG2DGRxqvknbrDd7m6rDjwKhAg6qzEtffkUk9ismhnEISFJEEDsiiDM8OGcQpAbdLBbgUyFd+QWOahjZHlECEBXaAbx9/OxUb4b/MmSm1gyoB3hRKRk3+kb/mh/w9f8M/8e9/zVWoHGUvI1h7ohVJd+bp1fWv/1WFsJK83yoomv/oWpJLS6pbH90niinncCYZho+fHa7fWWsWc/wl/4wJXvAD/hYzRMMvzqtVsfZcdZQqjaBHauZQdRHhlgv4MlToweeCy3EfEpkLVPJoWN4oFmgcXddxsHmrbfC2sbrYWH5YrXKKrtENamFft2mZ7tMKdcjRlrQ9ra95tW/6dX1Ob01Ca1qluUJ/HN34AUy92YQ=</latexit> <latexit sha1_base64="2l9vxtczbdtNcL2km7KN9s7Myxs=">AAADC3ichVE9axRBGH6z8SPGj5yxEWwGj5MIeswGQRGEgI2Nkq9LAtl47O7N3g2Z/WBn7uRc7g8I1hZWChZiaSd2IqZIa5GfIHZGsDCFz86tiAZ1jtt55nnmeT/mDTIlteF8b8KZPHL02PGpE9MnT50+M1M7O7um034eilaYqjTfCHwtlExEy0ijxEaWCz8OlFgPtm+X+vpA5FqmyaoZZmIr9ruJjGToG1DtWuQFqeroYYyNFcwTxmcjdot5SkRmbnxuQ3DBXgHbSY0uwU/+LrtaaZx5uez2zGV2vwwU+6aXx0CrUEftWp03uV3sMHArUKdqLaa1D+RRh1IKqU8xCUrIACvySeO3SS5xysBtUQEuB5JWFzSiaXj7uCVwwwe7jW8Xp82KTXAuY2rrDpFF4Z/DyajBP/KXfJ/v8Ff8Ez/4a6zCxihrGWIPxl6RtWcenV/59l9XjN1Q75cLjsY/qjYU0Q1brUT1mWXKPsJxhMHDJ/srN5cbxSX+nH9GB8/4Hn+HHpLB1/DFklh+aivKrUfQA9tzbKtI8MoFNI0MHWgRuD7ewyBygUw9GpQvigG6f47rMFibb7q86S5dqy/cq0Y5RRfoIs1hXtdpge7QIrWQfZe+0Hc6cB47r503ztvxVWei8pyj35bz/gc8qbpW</latexit> <latexit sha1_base64="pYtNZg2paon8StH4xBwbnoJgSFY=">AAACr3ichVHLThRRED00KAOoDLoxcUOcjGE1qSYkEFYkblwRXsOQMIDdTQ1zQ7/SfWdg7PADfoAuXCgmLoif4UJ+wAWfYFxCwoYF1Xc6MULA6vS9dU/Vqacb+yrVRGcD1uDQg4fDpZHRsUePn4yXJ56up1En8bjuRX6UbLhOyr4Kua6V9nkjTtgJXJ8b7v7r3N7ocpKqKFzTvZi3AmcvVC3lOVqgZlPzoc4O2pzw0U65QjUyMnlbsQulgkKWovJPNLGLCB46CMAIoUX34SCVbxM2CLFgW8gES0RTxs44wqhwO+LF4uEIui/nnrw2CzSUdx4zNWxPsvjyJ8KcRJV+0Qmd0yl9p990dWeszMTIa+nJ7fa5HO+Mv3++evlfViC3RvsvSxjVe6rWaGHOVKuk+tggeR9eP0L33cfz1fmVavaKvtIf6eCYzuiH9BB2L7xvy7zyyVSUGA7jwPQcmCpCmXImtlQy7IqtJVhH5qElciaZ2ujmE5UF2jfXdVtZn67ZVLOXZyoLi8UqS3iBl5iSfc1iAW+whLpkj/EBn/HFsq2GtW297btaAwXnGf4RS10DCm2ccg==</latexit> <latexit sha1_base64="xfnw6cCyV3er5ZC/e8yWGIYXLko=">AAADbnichVHLahRREK2e9hHHR0YFEUS8OEyYII63RVAEIeDGjZKHkwTSydDdc3u6mX7RfXvM2MwP+AMuXCm4ED/DhfoBLvIJ4kaI4MaFp++0CSY+7jBdVefUqVt1y04CP5Oc72g1/cjRY8dnTtRPnjp9ZrZx9txqFuepI7pOHMTpum1lIvAj0ZW+DMR6kgortAOxZg/vl/zaSKSZH0eP5TgRm6E1iHzXdywJqNf4aIaW9GyXFSxnE9Zm+/E24nk2d+8AZJp17895BjhWH5SkHQf9bBzCIMEU0tqrFQhXtpF6jZlZHrIe+CErtRO2Bf8hu658U2wnv5KVfpoIIvUHnpzfs6VISXqNJu9wddhhx6icJlVnMW68J5P6FJNDOYUkKCIJPyCLMvw2yCBOCbBNKoCl8HzFC5pQHdocWQIZFtAhvgNEGxUaIS5rZkrt4JYA/xRKRi3+ib/hu/wDf8s/8x9/rVWoGmUvY1h7qhVJb/bZxZXv/1WFsJK8fRUUrX90LcmlO6pbH90nCinncKYVRk+f767cXW4Vc/wV/4IJXvId/g4zRKNvzuslsfxCdZQqjaAnauZQdRHhlQtwGW7og3OB5XgPicoFbvJoVL4oFmgcXNdhZ/Vmx+AdY+lWc+FRtcoZukRXqY193aYFekCL1CVHu6F1tS2tV/uqX9Av61emqTWt0pyn347e/glcRtHm</latexit>
- 10. 1変数ガウス分布(1/2) ? ?|?, ?( = 1 2??( ?. ( exp ? 1 2?( ? ? ? ( = 1 2??( ?. ( exp ? 1 2?( ?( + ? ?( ? ? 1 2?( ?( = 1 2??( ?. ( exp ? 1 2?( ?( exp ? 1 2?( ?( + ? ?( ? = 1 2??( ?. ( exp ? 1 2?( ?( exp ?? ?( ? ?1 2?( 4 ? ?(
- 11. 1変数ガウス分布(2/2) つまり、1変数ガウス分布も以下の対応付けによって 指数型分布族であるといえる ? = ?? ?( ??1 2?( ? ? = ? ?( ? ? = 2? ?8. ( ? ? = ?2?( ?. ( ??? ?. ( 4?(
- 12. 目次 2.4 指数型分布族 ? 2.4.1 最尤推定と?分統計量 ? 2.4.2 共役事前分布 ? 2.4.3 無情報事前分布
- 13. 最尤推定量と十分統計量(1/4) パラメータベクトルηの推定をする ηについて勾配をとる { } { }T T ( ) ( )exp ( ) ( ) ( )exp ( ) ( ) 0h d h dh h h h? + =ò òx u x x x u x u x xg g { }T ( ) ( )exp ( ) 1h dh h =ò x u x xg (2.195) 両辺を(2.195)で割る { } [ ]T( ) ( ) ( )exp ( ) ( ) ( ) ( ) h d h h h h ? - = =ò x u x u x x Ε u x g g g
- 14. 最尤推定量と十分統計量 (2/4) 演習(2.58) また、共分散については より、?次微分から得られる 指数型分布族の分布を正規化できたなら、微分で簡単に分布の モーメントがわかる [ ] { } { } { } [ ] [ ] T T T T T T ln ( ) ( ) ( ) ( )exp ( ) ( ) ln ( ) ( ) ( )exp ( ) ( ) ( ) ( )exp ( ) ( ) ( ) ( ) ( ) ( ) ( ) cov ( ) h d h d h d h h h h h h h h -? = = -?? = ? + é ù é ù= - +? ? ? ? = ò ò ò Ε u x x u x u x x x u x u x x x u x u x u x x Ε u x Ε u x Ε u x u x u x g g g g g [ ]ln ( ) ( )h-? = Ε u xgつまり、 が得られる (2.226)
- 15. 最尤推定量と十分統計量(3/4) 同分布に従う独?なデータの集合 { }1, , N=X x x! ( ) T 11 | ( ) ( ) exp ( ) N N N n n nn p hh h h == ? ? ì ü = í ?? ÷ ? ?è ? ??X x u xg尤度関数 対数尤度関数 ( ) T 1 1 ln | ln ( ) ln ( ) ( ) N N n n n n p h Nh h h = = = + +? ?X x u xg ( )ln |p hX のηについて勾配を0とすると、 原則として、 この式をとけば最尤推定量?=>が 得られる。1 1 ln ( ) ( ) N ML n nN h = -? = ?u xg (2.227)
- 16. 最尤推定量と十分統計量(4/4) 1 1 ln ( ) ( ) N ML n nN h = -? = ?u xg 最尤推定解は に依存する( )nn? u x ? → ∞の極限では… 上式の右辺は [ ]( )Ε u x になるため、(2.226)から最尤推定量が 真の値に等しくなることがわかる ベイズ推論においてもこの?分性が成?する(8章にて)
- 17. 目次 2.4 指数型分布族 ? 2.4.1 最尤推定と?分統計量 ? 2.4.2 共役事前分布 ? 2.4.3 無情報事前分布
- 18. 共役事前分布(1/2) ?般に、ある確率分布 ?(?|?) について、事後分布がその事前分布と同じ関数形に なるような尤度関数と事前分布 ?(?) を求めることは可能である。 指数型分布族 の共役事前分布とは (2.194) : 正規化係数 : (2.194)のものと同じ ? ?|?, ? = ? ?, ? ? ? Gexp ??H ? ? ?, ? ? ?
- 19. 共役事前分布(2/2) 尤度関数(2.227)と事前分布(2.229)の積を確認する 尤度関数 事前分布 事後分布をみると, 事前分布のパラメータνは 有効な事前の仮想観測値χの数だとみなせる ? ?|?, ?, ? ∝ ? ? GKLexp ?H M NO. L ? ?N + ??
- 20. 目次 2.4 指数型分布族 ? 2.4.1 最尤推定と?分統計量 ? 2.4.2 共役事前分布 ? 2.4.3 無情報事前分布
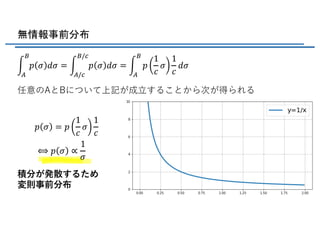
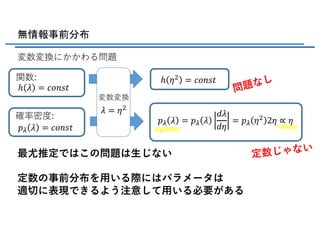
- 22. 無情報事前分布 とりあえず?様分布に… 離散変数であれば可能 しかし 連続では?つの問題が… パラメータ で定められる分布 を考える 影響の少ない事前分布を選びたい ? ? ?|? ? ? = ?????
- 23. 無情報事前分布 連続パラメータλで を?いる際の?つの問題 1. λの定義域が有界でないとき、λ上での積分が発散する (正規化できない) 2. ?線形の変数変換をすると定数にならない ? ? = ?????
- 25. 無情報事前分布 変数変換にかかわる問題 関数: 問題なし 確率密度: 変数変換 定数じゃない 最尤推定ではこの問題は?じない 定数の事前分布を?いる際にはパラメータは 適切に表現できるよう注意して?いる必要がある ? = ?( ? ? = ????? ? ?( = ????? ?V ? = ????? ?V ? = ?V ? ?? ?? = ?V ?( 2? ∝ ?
- 26. 無情報事前分布 平?移動不変性 モデル(尤度関数) : : 位置パラメータ 定数分だけ移動した においても、 ただし 新しい変数においても 確率密度は形状が同じ ? ?|? = ? ? ? ? ? X? = ? + ? ? X?| ?? = ? X? ? ?? X? ≡ ? + ?
- 27. 無情報事前分布 事後分布 事前分布?(?)尤度関数? ? ?∝ × 平?移動不変性 事前分布にも平?移動不変性を 任意の定数cに対してμが区間 に?る確率と 区間 に?る確率が等しくなければならない ? ≤ ? ≤ ? ? ? ? ≤ ? ≤ ? ? ?
- 28. 無情報事前分布 任意のAとBについて上記が成?することから次が得られる 位置パラメータの例 ガウス分布の平均パラメータμなど ? ? ? ? = ? ? ? ? ? = ?????
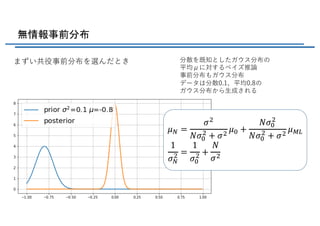
- 29. 無情報事前分布 まずい共役事前分布を選んだとき 分散を既知としたガウス分布の 平均μに対するベイズ推論 事前分布もガウス分布 データは分散0.1、平均0.8の ガウス分布から?成される ?L = ?( ??b ( + ?( ?b + ??b ( ??b ( + ?( ?=> 1 ?L ( = 1 ?b ( + ? ?(
- 31. 無情報事前分布 尺度不変性 新しい変数においても 確率密度は形状が同じ定数倍だけ拡?縮?した においても、 ただし モデル(尤度関数) : : 尺度パラメータ [m]から[km]への 尺度の変換などともとれる ? ?|? = 1 ? ? ? ? ? X? = ?? ? X?| X? = 1 X? ? X? X? X? ≡ ??
- 32. 無情報事前分布 再掲 事後分布 事前分布?(?)尤度関数? ? ?∝ × 尺度不変性 事前分布にも尺度不変性を 任意の定数cに対してμが区間 に?る確率と 区間 に?る確率が等しくなければならない ? ≤ ? ≤ ? ?/? ≤ ? ≤ ?/?
- 33. 無情報事前分布 任意のAとBについて上記が成?することから次が得られる 積分が発散するため 変則事前分布 e f g ? ? ?? = e f/h g/h ? ? ?? = e f g ? 1 ? ? 1 ? ?? ? ? = ? 1 ? ? 1 ? ? ? ? ∝ 1 ?
- 34. 無情報事前分布 に?る確率と に?る確率は 等しくなる パラメータの対数を考えたほうが便利なことも 新しい変数η : (1.27)より さらに、 よって ? = ln ? ?k ? = ?l ? ?? ?? = ?l ln ? 1 ? ? ? ∝ 1 ? ? ln ? = ????? 10 ≤ ? ≤ 100 100 ≤ ? ≤ 1000
- 35. 無情報事前分布 尺度パラメータの例 : 位置パラメータ考慮済みのガウス分布の標準偏差σ ただし、 精度をつかうなら(1.27)から ? ?|?, ?( ∝ ?8. ??? ? ?o? ? ( o? = ? ? ? ? = ?1 ?( , ?k ? = ?V ? ?? ?? = ??V ? 3 ?q ∝ 1 ? ??V ? 3 ?( = ????? ? ? ? ∝ ?( = 1 ?
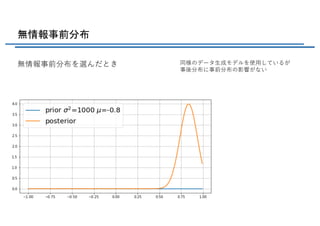
- 36. 無情報事前分布 の共役事前分布は(2.146)のガンマ分布 0 0 0a b= = とすると無情報事前分布に (2.150)および(2.151)参照 0 2 N N a a= + データ由来の項のみに依存することがわかる ??? ?|?b, ?b? ?L = ?b + ? 2 ?=> (




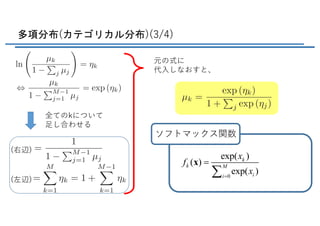




![最尤推定量と十分統計量(1/4)
パラメータベクトルηの推定をする
ηについて勾配をとる
{ } { }T T
( ) ( )exp ( ) ( ) ( )exp ( ) ( ) 0h d h dh h h h? + =ò òx u x x x u x u x xg g
{ }T
( ) ( )exp ( ) 1h dh h =ò x u x xg (2.195)
両辺を(2.195)で割る
{ } [ ]T( )
( ) ( )exp ( ) ( ) ( )
( )
h d
h
h h
h
?
- = =ò x u x u x x Ε u x
g
g
g](https://image.slidesharecdn.com/prml2-191127174227/85/PRML-2-4-13-320.jpg)
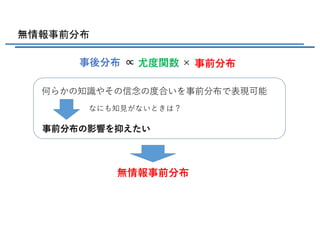
![最尤推定量と十分統計量 (2/4) 演習(2.58)
また、共分散については
より、?次微分から得られる
指数型分布族の分布を正規化できたなら、微分で簡単に分布の
モーメントがわかる
[ ] { }
{ } { }
[ ]
[ ]
T
T T T
T T
ln ( ) ( ) ( ) ( )exp ( ) ( )
ln ( ) ( ) ( )exp ( ) ( ) ( ) ( )exp ( ) ( ) ( )
( ) ( ) ( ) ( )
cov ( )
h d
h d h d
h h h
h h h h h
-? = =
-?? = ? +
é ù é ù= - +? ? ? ?
=
ò
ò ò
Ε u x x u x u x x
x u x u x x x u x u x u x x
Ε u x Ε u x Ε u x u x
u x
g g
g g g
[ ]ln ( ) ( )h-? = Ε u xgつまり、 が得られる (2.226)](https://image.slidesharecdn.com/prml2-191127174227/85/PRML-2-4-14-320.jpg)

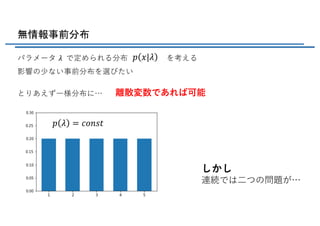
Ε u x になるため、(2.226)から最尤推定量が
真の値に等しくなることがわかる
ベイズ推論においてもこの?分性が成?する(8章にて)](https://image.slidesharecdn.com/prml2-191127174227/85/PRML-2-4-16-320.jpg)





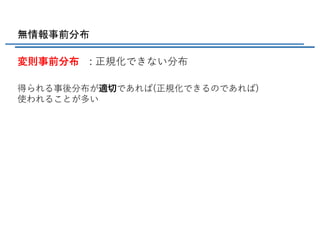



![無情報事前分布
尺度不変性
新しい変数においても
確率密度は形状が同じ定数倍だけ拡?縮?した においても、
ただし
モデル(尤度関数) :
: 尺度パラメータ
[m]から[km]への
尺度の変換などともとれる
? ?|? =
1
?
?
?
?
?
X? = ??
? X?| X? =
1
X?
?
X?
X?
X? ≡ ??](https://image.slidesharecdn.com/prml2-191127174227/85/PRML-2-4-31-320.jpg)