パターン認識と機械学習 §8.3.4 有向グラフとの関係
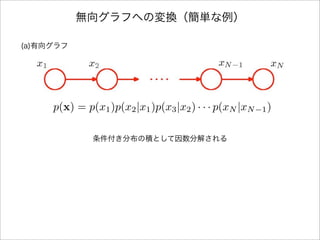
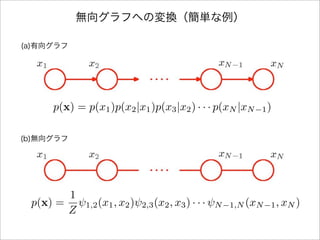
- 4. 無向グラフへの変換(簡単な例) (a)有向グラフ p(x) = p(x1)p(x2|x1)p(x3|x2) · · · p(xN |xN 1) 条件付き分布の積として因数分解される
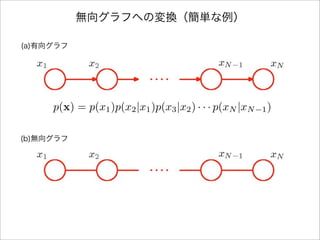
- 5. 無向グラフへの変換(簡単な例) (a)有向グラフ (b)無向グラフ p(x) = p(x1)p(x2|x1)p(x3|x2) · · · p(xN |xN 1)
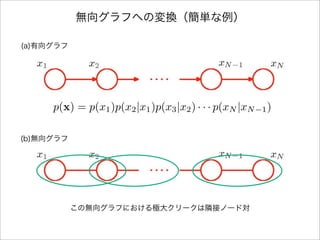
- 6. 無向グラフへの変換(簡単な例) (a)有向グラフ (b)無向グラフ p(x) = p(x1)p(x2|x1)p(x3|x2) · · · p(xN |xN 1) この無向グラフにおける極大クリークは隣接ノード対
- 7. 無向グラフへの変換(簡単な例) (a)有向グラフ (b)無向グラフ p(x) = p(x1)p(x2|x1)p(x3|x2) · · · p(xN |xN 1) p(x) = 1 Z 1,2(x1, x2) 2,3(x2, x3) · · · N 1,N (xN 1, xN )
- 8. 無向グラフへの変換(簡単な例) p(x) = p(x1)p(x2|x1)p(x3|x2) · · · p(xN |xN 1) p(x) = 1 Z 1,2(x1, x2) 2,3(x2, x3) · · · N 1,N (xN 1, xN ) このような対応付けができる
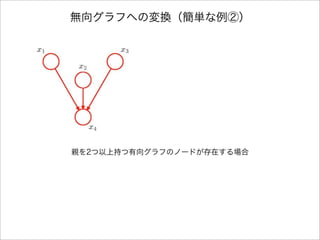
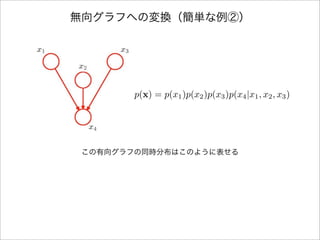
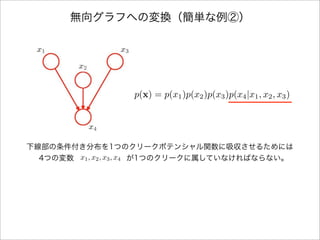
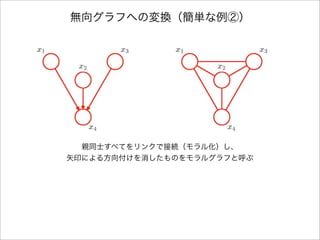
- 11. 無向グラフへの変換(簡単な例②) 下線部の条件付き分布を1つのクリークポテンシャル関数に吸収させるためには ?4つの変数???????が1つのクリークに属していなければならない。 p(x) = p(x1)p(x2)p(x3)p(x4|x1, x2, x3) x1, x2, x3, x4
- 13. 有向グラフを無向グラフに変換するには ? グラフの各ノードに対してそのすべての親同士の対に無 向リンクを付加する。 ? もともとのリンクから矢印の方向性を取り除いてモラ ルグラフを作る。 ? モラルグラフのすべてのクリークポテンシャル関数を1 に初期化する。 ? もともとの有向グラフの条件付き分布因子を1つ取って きて、対応するクリークポテンシャルの1つに掛ける。 モラル化とは、リンクの追加を最小限に抑えることによって 条件付き独立性をできる限り残す方法である。
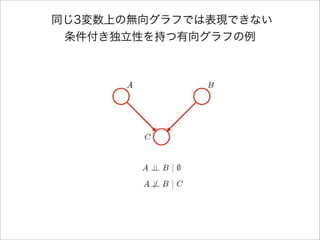
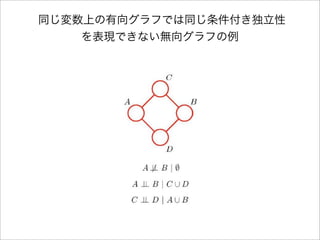
- 14. 依存性マップ ? あるグラフが、ある分布が満たす条件付き独立性をも れなく表現するとき、そのグラフをその分布に対する 依存性マップ(dependency map、D-map)と言う。 ? 全くリンクのない完全に分離されたグラフは、すべて の分布に対する自明な依存性マップである。
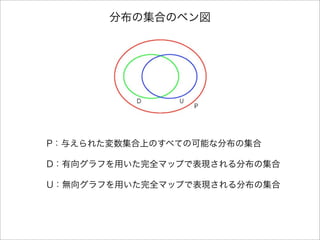
- 16. 完全マップ ? ある分布の条件付き独立性があるグラフによってすべ て表現され、逆にそのグラフが表現するすべての条件付 き独立性をその分布が満たすならば、そのグラフをそ の分布の完全マップ(perfect map)と言う。 ? つまり、完全マップは独立性マップでありかつ依存性 マップでもある。
- 20. 連鎖グラフ ? グラフィカルモデルの枠組みは、有向リンクと無向リ ンクを両方持つグラフにも矛盾なく拡張できる。 ? そのようなグラフは連鎖グラフと呼ばれる。 ? 有向グラフおよび無向グラフは連鎖グラフの特別な場 合として含まれる。 ? 連鎖グラフを用いても完全マップを作れない分布が存 在する。 PRMLでは、連鎖グラフについてはこれ以上議論しない。
- 21. ご清聴ありがとうございました。