狠狠撸

Probabilistic Graphical Models 輪読会
Chapter 5 Local Probabilistic Models
島田大樹

この章について
様々な条件付き確率分布 ?CPD?とその独立性について考える
tbd

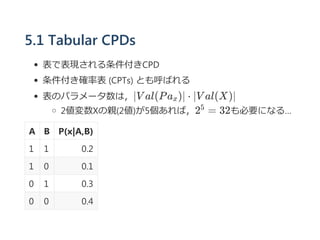
5.1 Tabular CPDs
表で表現される条件付きCPD
条件付き確率表 ?CPTs? とも呼ばれる
表のパラメータ数は，∣V al(Pa )∣ ? ∣V al(X)∣
2値変数Xの親?2値?が5個あれば，2 = 32も必要になる…
A B P?x|A,B?
1 1 0.2
1 0 0.1
0 1 0.3
0 0 0.4
x
5

5.2 Deterministic CPDs
5.2.1 Representation
変数Xがその親の決定的な関数になっているCPD
f : V al(Pa ) ? V al(X)があるとき，以下のようなCPD
P(x∣Pa ) =
関数fは，たとえば
[2値変数] 親同士の or / and
[連続値変数] X = Y + Z など
X
X {
1
0
x = f(Pa )X
otherwise

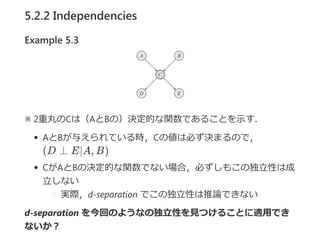
5.2.2 Independencies
Example 5.3
※ 2重丸のCは（AとBの）決定的な関数であることを示す．
AとBが与えられている時，Cの値は必ず決まるので，
(D ⊥ E∣A, B)
CがAとBの決定的な関数でない場合，必ずしもこの独立性は成
立しない
実際，d‐separation でこの独立性は推論できない
d‐separation を今回のようなの独立性を見つけることに適用でき
ないか？

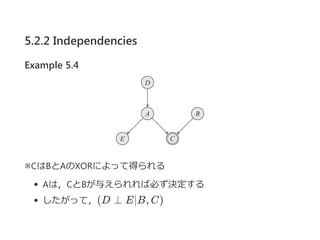
(X ⊥ Y ∣Z) という場合を考える．
deterministic CPDを持っている，かつ
その親PaX がすべて与えられている (Z の部分集合)
変数 X を観測可能であるとして，逐次的にZ に追加して
d‐separationを計算する
i
+
i
+

定理5.1
Gをネットワークの構造，D, X, Y , Zを変数の集合とする．
Zが与えられた時XがY と deterministically separated なら，
P ?I (G) のようなすべての分布Pと，
決定的条件付き確率分布P(X∣Pa )，X ∈ Dのそれぞれに
ついて，P ? (X ⊥ Y ∣Z)を得る．
証明は?exercise 5.1?
この方法で，全ての決定的関数を含む独立性を得られるか？
l
X

定理5.2
Gをネットワークの構造，D, X, Y , Zを変数の集合とする．
DET‐SEP(G, D, X, Y , Z)が偽なら，
P ?I (G) のような分布Pが存在していて，
決定的条件付き確率分布P(X∣Pa )，X ∈ Dでも，
P ? (X ⊥ Y ∣Z)ではない．
DET‐SEPは親の決定的関数になっている変数から単に由来する
独立性は，見つけることができる．
しかし，特別な決定的関数は他の独立性をつくることがある
l
X

Example 5.4
※CはBとAのXORによって得られる
Aは，CとBが与えられれば必ず決定する
したがって，(D ⊥ E∣B, C)

Revisit Example 5.3 (Example 5.5)
※ Cは（AとBの）OR関数
A = a の時，Cは親のORをとるので，Bの値に関係なく決定
したがって，P(D∣B, a ) = P(D∣a )．（BとDは独立）
A = a の時では，Cはまだ決定しないので，上記は成立せず
決定的な変数は，特別な形の独立を持つため，本書では，
P(X∣Y , Z) = P(X∣Z)と仮定した(X ⊥ Y ∣Z)の形式のも
のに限定する．
1
1 1
0

Definition 5.1
X, Y , Zを互いに素な変数集合，Cを変数集合（
X ∪ Y ∪ Zと素でなくてもよい），cをc ∈ V al(C)とす
る．
P(X∣Y , Z, c) = P(X∣Z, c)whereneverP(Y , Z, c) > 0
ならば，
Zと，(X ⊥ Y ∣Z, c)で示されるコンテキストcが与えられた
下でXとY が contextually independentであるという．
この形の独立を context‐specific independencies ?CSI?と呼ぶ．
c

Revisit Example 5.3 with CSI (Example 5.6)
※ Cは（AとBの）OR関数
A = a のときには，Bを観測せずともC = c が決定した
したがって，(C ⊥ B∣a )，(D ⊥ B∣a )
C = c のときには，A = a もB = b も決定する
したがって，(A ⊥ B∣c )，(D ⊥ E∣c )
C = c ，B = b のときには，A = a が決定する
したがって，(D ⊥ E∣b , c )
1 1
c
1
c
1
0 0 0
c
0
c
0
1 0 1
c
0 1

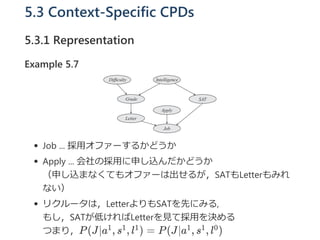
5.3 Context-Specific CPDs
5.3.1 Representation
Example 5.7
Job ... 採用オファーするかどうか
Apply ... 会社の採用に申し込んだかどうか
（申し込まなくてもオファーは出せるが，SATもLetterもみれ
ない）
リクルータは，LetterよりもSATを先にみる,
もし，SATが低ければLetterを見て採用を決める
つまり，P(J∣a , s , l ) = P(J∣a , s , l )1 1 1 1 1 0

5.3.1.1 Tree-CPDs
Example 5.7 with Tree-CPD (Example 5.8)
あるJの確率を知りたければ，木の根から順番に各属性を
"テスト"すれば良い
ex.? P(J∣a , s , l )は，
J : P(j ) = 0.1, and?P(j ) = 0.9
1 1 0
0 1

5.3.1.1 Tree-CPDs
Definition 5.2
根が1つ ?rooted tree?
各tノードは葉か内部tノードを持つ
葉はP(X)を表す
内部tノードはZ ∈ Pa なある変数Zを表す
各内部tノードは，子への弧?arc, エッジ?の集合を持つ
それぞれ，変数割当てZ = z ?for?z ∈ V al(Z)を表す
枝βは根から葉までの経路を表す
枝は，同じ変数を示す内部tノードを2つ以上持たない
X
i i

5.3.1.1 Tree-CPDs
Example 5.9
親コンテキスト<a >は，申し込まなかった場合に対応する
親コンテキスト<a , s >は，高いSATスコアの人が採用に応募
した場合に対応する
テーブル記法では8つのパラメータが必要だが，
木記法では4つのみでよい！
tree‐CPDはある変数が，大量の変数群のうち一つだけに依存
するような場合には有効な方法
0
1 1

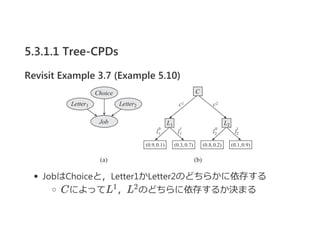
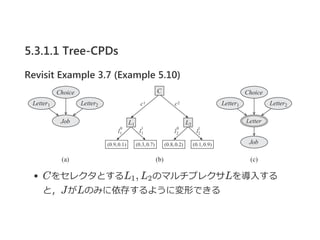
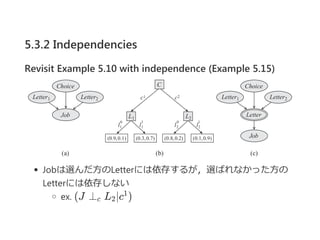
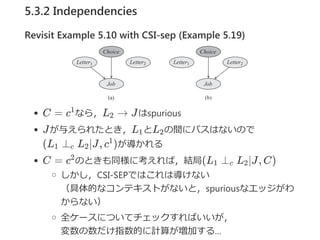
5.3.1.1 Tree-CPDs
JobはChoiceと，Letter1かLetter2のどちらかに依存する
CによってL ，L のどちらに依存するか決まる1 2

5.3.1.1 Tree-CPDs
前ページのようなCPDを multiplexer CPDによって形式化する
Definition 5.3
V al(A) = {1, ..., k}かつ，
P(Y ∣a, Z , ..., Z ) = 1 {Y = Z } ならば，
CPD P(Y ∣A, Z , ..., Z )は multiplexer CPD という．
multiplexer CPDは，条件に応じて特定の親をスイッチする
ex.10ではChoiceによって依存関係がスイッチされている
1 k a
1 k

5.3.1.1 Tree-CPDs
CをセレクタとするL , L のマルチプレクサLを導入する
と，JがLのみに依存するように変形できる
1 2

5.3.1.1 Tree-CPDs
木記法は，CPDのコンテキストの特性を表現するのに，有用な
枠組み
データセットから木構造を学習する手法も応用できる
木記法は，単一のデータ構造を持つCPDを表現する手法
依存構造をより細かい要素に落とし込みたい場合，あま
り向かない

5.3.1.2 Rule CPDs
Definition 5.4 rule
ルールρは，?c; p?で構成される．
ここで，cは変数集合Cのある部分集合への割当てであり，
p ∈ [0, 1]である．
CはScope[ρ]で表される，ρのスコープである．

5.3.1.1 Tree-CPDs
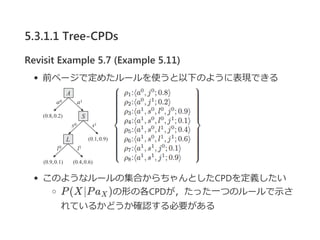
前ページで定めたルールを使うと以下のように表現できる
このようなルールの集合からちゃんとしたCPDを定義したい
P(X∣Pa )の形の各CPDが，たった一つのルールで示さ
れているかどうか確認する必要がある
X

5.3.1.2 Rule CPDs
Definition 5.5 rule‐based CPD
rule‐based CPD P(X∣Pa )とは，
以下のようなルール集合Rである．
各ルール ρ ∈ Rについて，Scope[ρ] ? {X} ∪ Pa
{X} ∪ Pa への各割当て(x, u)について，
cが(x, u)と一致するようなルール?c; p? ∈ Rがひとつだ
けある
P(X∣U)は， P(x∣u) = 1を満たす適当なCPD
前ページのExample 5.11はこの定義を満たしている
X
X
X
∑x

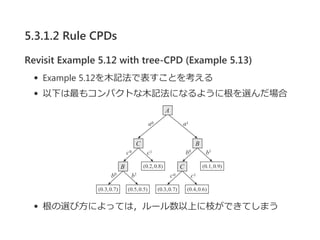
5.3.1.2 Rule CPDs
Example 5.12
XをPa = {A, B, C}を親に持つ変数とし，
XのCPDを以下ののルール集合から定義する
以下のようなCPDが定義できる
各列ごとに和をとれば，ちゃんと1になっている
X

5.3.1.2 Rule CPDs
Proposition 5.1
Bをベイジアンネットワーク，Bにおける各CPD P(X∣Pa )
がルール集合R として表現されているとする．
Rは∪ R として定義される多重集合である．
ここで，∪ は多重集合和であり，重複を含む全てのルールイ
ンスタンスを持っている．
そして，ネットワーク変数Xへの任意の割当てξの確率は,
P(ξ) = p
として計算される．
X
X
X∈X
+
X
+
∏?c;p?∈R,ξ～c

5.3.1.2 Rule CPDs
Revisit Example 5.12 with tree-CPD (Example 5.13)
Example 5.12を木記法で表すことを考える
以下は最もコンパクトな木記法になるように根を選んだ場合
根の選び方によっては，ルール数以上に枝ができてしまう

5.3.1.3 Other Representatioins
枝やルールを拡張した表現を考えることもできるが，一般に
定式化が複雑になる．
decision diagram
木表記において，子ノードの共有を許容して冗長な部分
木の発生を防ぐ方法

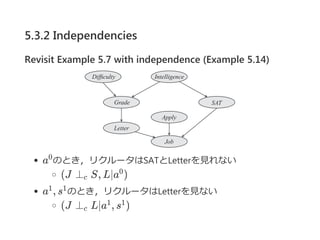
5.3 Context-Specific CPDs
"a のとき，リクルータは変数SとLに依らずに採用オファー
を決める"
context‐specificな独立をもつCPDを表現している
このようなCPDの構造では，ネットワーク全体を見ない，
局所的な独立を推論することができる
context‐specific CPDによって表現される独立性を考える
0

Revisit Example 5.7 with independence (Example 5.14)
a のとき，リクルータはSATとLetterを見れない
(J ⊥ S, L∣a )
a , s のとき，リクルータはLetterを見ない
(J ⊥ L∣a , s )
0
c
0
1 1
c
1 1

cをtree‐CPDのある枝で表現されるコンテキストとしたとき，
Xは(Pa ? Scope[c])と独立
Pa = {A, S, L}
Scope[c] = {A}, ?(J ⊥ S, L∣a )
Scope[c] = {A, S}, ?(J ⊥ L∣a , s )
X
J
c
0
c
1 1

Revisit Example 5.10 with independence (Example 5.15)
Jobは選んだ方のLetterには依存するが，選ばれなかった方の
Letterには依存しない
ex. (J ⊥ L ∣c )c 2
1

Revisit Example 5.14 with rule (Example 5.16)
s というコンテキストが与えられた時，
s はaについてのコンテキストを含む
(J ⊥ L∣s )
Xの親Y についてのルールがないなら，Xはcが与えられたと
きY と独立である
1
1
c
1

Deifinition 5.6 reduced rule
ρ = ?c ; p?をルール，C = cをコンテキストとする．
c がcと一致するなら，ρ ～ cという．
この場合，c = c ?Scope[c ] ? Scope[c]?を
Scope[c ] ? Scope[c]の変数からc への割当てとする．
そして，reduced rule ρ[c] = ?c ; p?を定義する．
ルール集合 R について，reduced rule 集合
R[c] = {ρ[c] : ρ ∈ R, ρ ～ c}
が定義される．
′
′
′′ ′ ′
′ ′
′′

Revisit Example 5.12 with reduced rule (Example 5.17)
Example 5.12のR[a ]は，
となる．
a と一致するルールのみが残り，ルールからa が削除される
1
1 1
?

Proposition 5.2 reduced rule
Rを変数Xについてのrule‐based CPDのルール集合とし，
R をRのうちcと一致するルール集合とする．
Y ? Pa を，Y ∩ Scope[c] = ?のようなXの親のある部
分集合とする．
各ρ ∈ R[c]について，Y ∩ Scope[ρ] = ?ならば，
(X ⊥ Y ∣Pa ? Y , c) である．
（証明はexercise 5.4）
ルール記法から"局所的な"CSIを推論する計算手法
変数Y が，あるコンテキストについての reduced rule 集合に
含まれるかどうか，ルール数の線形時間で確認できる
c
X
c X

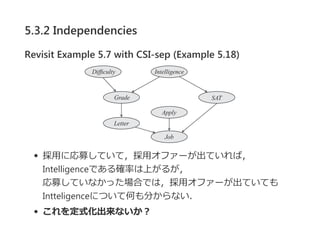
Revisit Example 5.7 with CSI-sep (Example 5.18)
採用に応募していて，採用オファーが出ていれば，
Intelligenceである確率は上がるが，
応募していなかった場合では，採用オファーが出ていても
Intteligenceについて何も分からない．
これを定式化出来ないか？

A = a のコンテキストを考える
このコンテキストでは，S → J, L → Jの両方のエッジがな
くなる
これらのエッジがないグラフで d‐separationをチェックす
ればよさそう
0

Deifinition 5.7 spurious edge
P(X∣Pa )をCPD，Y ∈ Pa ，cをコンテキストとする．
P(X∣Pa )が(X ⊥ Y ∣Pa ? {Y }, c )を満たすなら，
エッジY → Xは，cにおいて擬似的? spurious ?と呼ぶ．
ここで，c = c?Pa ?はPa の変数集合に対するcの制約で
ある．
CPDがルールによって表現されているとき，
reduced rule 集合を確認することによって
エッジが spurious であるかどうか決定できる
Y が reduced rule集合R[c]に出現しないなら，
cにおいてY → Xは spurious
X X
X c X
′
′
X X

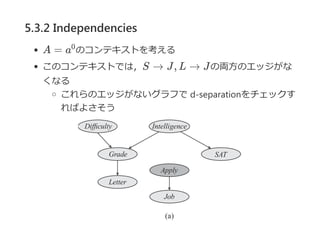
CSI‐separation
ここで，CSI‐separation を定義できる
CSIを考慮したd‐separation
擬似的なエッジを取り除く局所的な操作をして，
得られたグラフに诲‐蝉别辫补谤补迟颈辞苍を适用する

S → J, L → Jは spurious で，?a?のグラフが得られる
?a?のグラフでJとI，JとDはd‐separated
したがって，CSI‐SEPを用いることで，
a が与えられたとき，JとIがa のときにd‐separatedだと得
られた
?b?はa , s のときに得られるグラフ
0 0
1 1

CSI‐separationはcontext‐specificな独立を決定するためのテス
トに用いることが出来る
Theorem 5.3
G をネットワーク構造，PをP ?L (G)な分布，cをコンテ
キスト，X, Y , Zを変数集合とする．
Xがcの下でZが与えられたときにY とCSI‐separatedなら，
P ? (X ⊥ T∣Z, c)
l
c

C = c なら，L → Jはspurious
Jが与えられたとき，L とL の間にパスはないので
(L ⊥ L ∣J, c )が導かれる
C = c のときも同様に考えれば，結局(L ⊥ L ∣J, C)
しかし，CSI‐SEPではこれは導けない
（具体的なコンテキストがないと，spuriousなエッジがわ
からない）
全ケースについてチェックすればいいが，
変数の数だけ指数的に計算が増加する…
1
2
1 2
1 c 2
1
2
1 c 2

5.4 Independence of Causal Influence
局所確率モデルにおける異なる種類の構造をみていく
noisy‐or model
generalized linear model

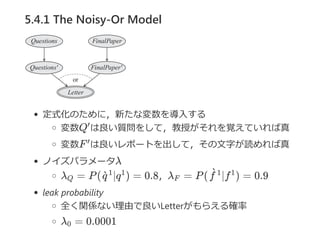
5.4.1 The Noisy-Or Model
教授が学生の推薦状（Letter）を書く例を考える
Letterの良さは，
良い質問をしていたか ?Question?
最終レポートの成績 ?Final paper?
できまり，学生は両方とも良い推薦状をもらうに十分だが
その学生の印象があまり残っていない場合
字が汚くてレポートが読めない場合
といったノイズを含む

2つの causal mechanism
教授が学生の授業態度や質問を覚えていた
P(l ∣q , f ) = 0.8
20%で質問を覚えていない
レポートの文字が読めた
P(l ∣q , f ) = 0.9
10%でレポートの字が読めない
質問も覚えていない，レポートの字も読めない確率は？
1 1 0
1 0 1

質問も覚えていない，レポートの字も読めない
0.2 ? 0.1 = 0.02
良い推薦状がもらえる確率
P(l ∣q , f ) = 0.981 1 1

定式化のために，新たな変数を導入する
変数Q は良い質問をして，教授がそれを覚えていれば真
変数F は良いレポートを出して，その文字が読めれば真
ノイズパラメータλ
λ = P( ∣q ) = 0.8，λ = P( ∣f ) = 0.9
leak probability
全く関係ない理由で良いLetterがもらえる確率
λ = 0.0001
′
′
Q q`1 1
F f`1 1
0

Definition 5.8 noisy‐or CPD
Y をk個の2値をとる親X , ..., X をもつ2値変数とする．
P(y ∣X , ..., X ) = (1 ? λ ) (1 ? λ )
P(y ∣X , ..., X ) = 1 ? [(1 ? λ ) (1 ? λ )]
となるk + 1個のノイズパラメータλ , λ , ..., λ があれば，
PCD P(Y ∣X , ..., X )はnoisy‐orである．
x を1, x を0と解釈すれば，以下のように変形できる．
P(y ∣X , ..., X ) = (1 ? λ ) (1 ? λ )
1 k
0
1 k 0 ∏i:X =xi i
1 i
1
1 k 0 ∏i:X =xi i
1 i
0 1 k
1 k
i
1
i
0
0
1 k 0
i=1
∏ i
xi

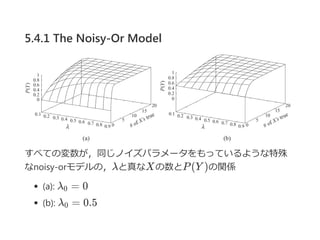
すべての変数が，同じノイズパラメータをもっているような特殊
なnoisy‐orモデルの，λと真なXの数とP(Y )の関係
?a?: λ = 0
?b?: λ = 0.5
0
0

5.4.2 Generalized Linear Models
causal influenceの独立性を満たす異なったモデルたちを
Generalized Linear Modelsとよぶ
多くのモデルが存在するが，ここではY がある不連続な有限
空間内の値を取る確率分布P(Y ∣X , ...X )を定義するモデル
を扱う
1 k

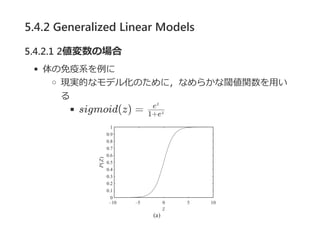
5.4.2.1 2値変数の場合
体の免疫系を例に
侵入者は体へ負担（burden）をかける
total burden ... どれくらい病気を引き起こしそうか
f(X , ..., X ) = w X
w はその負担がどれほど病気を引き起こすのに影響
するか
その負担が閾値を超えると，発熱やその他の感染症の症
状が出現しはじめる
f(X , ..., X )が閾値τを超えれば症状がでる
f(X , ..., X ) = w + w X
w = ?τ
1 k ∑i=1
k
i i
i
1 k
1 k 0 ∑i=1
k
i i
0

体の免疫系を例に
現実的なモデル化のために，なめらかな閾値関数を用い
る
sigmoid(z) = 1+ez
ez

Definition 5.9 logistic CPD
Y を，数値をとるk個の親X , ..., X をもつ2値変数とする．
P(y ∣X , ..., X ) = sigmoid(w + w X )
のようなk + 1個の重みw , w , ..., w があるなら，
CPD P(Y ∣X , ..., X )はlogistic CPDである．
パラメータwは，Y の対数オッズに及ぼす影響という解釈がで
きる．
2値変数のオッズ比はy とy の確率比なので，
O(X) = = = e
あるX が偽から真になったときの影響を考えると，
= = e
1 k
1
1 k 0 ∑i=1
k
i i
0 1 k
1 k
1 0
P(y ∣X ,...,X )0
1 k
P(y ∣X ,...,X )1
1 k
1/(1+e )z
e /(1+e )z z
z
j
O(X ,x )?j j
0
O(X ,x )?j j
1
exp(w + w X )0 ∑i≠j i i
exp(w + w X +w )0 ∑i≠j i i j wj

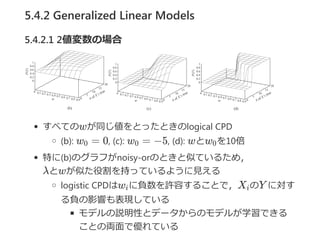
すべてのwが同じ値をとったときのlogical CPD
?b?: w = 0, ?c?: w = ?5, ?d?: wとw を10倍
特に?b?のグラフがnoisy‐orのときと似ているため，
λとwが似た役割を持っているように見える
logistic CPDはw に負数を許容することで，X のY に対す
る負の影響も表現している
モデルの説明性とデータからのモデルが学習できる
ことの両面で優れている
0 0 0
i i

5.4.2.2 多値変数の場合
Y をy , ..., y の複数の値を取るようにすることで，
logistic CPDを多値に拡張できる
Y の値の選択に，なめらかな"winner‐takes‐all"を用いる
あるy が1に近い値を取り，その他が0に近い値を取る
Definition 5.10 multinomial logistic PCD
Y を，k個の親X , ..., X をもつm値変数とする．
各j = 1, ..., mについて，
l (X , ..., X ) = w + w X
P(y ∣X , ..., X ) =
のようなk + 1個の重みw , w , ..., w があるなら，
CPD P(Y ∣X , ..., X )はmultinomial logistic CPDである．
1 n
i
1 k
i 1 k j,0 ∑i=1
k
j,i i
j
1 k exp(l (X ,...,X ))∑j =1′
m
j′ 1 k
exp(l (X ,...,X ))j 1 k
j,0 j,1 j,k
1 k

5.4.2.2 多値変数の場合
親X , X を持つ3値のY についてのモデルの例
親X が2値以上を取るような場合も扱える
X = x , ..., x なら，X = jのときX = x になる
2値変数X , ..., X を定義すれば良い
m値をとる親Xをもつ2値変数Y なら，m + 1個の重みを
使って
P(y ∣X) = sigmoid(w + w 1{X = x })
1 2
i
i i
1
i
m
i i,j i,j
1
i,1 i,m
1
0 ∑j=1
m
j
j

狠狠撸

Probabilistic Graphical Models 輪読会 Chapter5

More Related Content

Probabilistic Graphical Models 輪読会 Chapter5