Programación lineal
- 2. 1
- 3. 2
- 4. 3
- 5. 4
- 6. 5
- 7. 6
- 8. 7
- 9. 8
- 10. 9
- 11. 10
- 12. 11
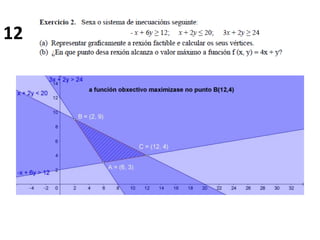
- 13. 12
- 14. 13 O máximo é no vértice C(40,5) e obtén un beneficio de 5700€
- 15. 14 O beneficio máximo 45300 € obtense repoboando 8ha de piñeiros e 25 ha de eucaliptos
- 16. 15 Máximo no (17,13) mÃnimo no (2,5)
- 17. 16
- 18. 17
- 19. 18
- 20. .O dono dunha tenda de fotografÃa desexa comercializar dous tipos de cámaras de fotos A e B cun prezo de venda ao público de 210€ e 300€ a unidade respectivamente. Dispón dun máximo de 2760€ para a compra das cámaras e as de tipo A valen a 120€ e as de tipo B a 180€ . O dono fará o pedido coa condición de que alomenos 3 cámaras sexan de tipo A e entre 4 e 12 sexan de tipo B, ademais o número de cámaras de tipo A non deben superar en máis de 3 unidades ao número de cámaras de tipo B. Formula o sistema de inecuacións asociado ao problema, representa a rexión factible e calcula os seus vértices, Cantas cámaras de cada tipo deberá adquirir para que os beneficios sexan máximos. 19
- 21. Representa a rexión definida polas seguintes inecuacións e determina os seus vértices. Calcula os valores máximo e mÃnimo que alcanza a función f(x.y)= 4x-3y+2 en dita rexión        ï€ï‚³ ï‚£ï€ ï‚£ï€«ï‚£  1232 643 92 0 xy xy yx y 20