Properties of Matter - U3 - Viscosity-PPT 1
- 1. Unit III - Viscosity Ms Dhivya R Assistant Professor Department of Physics Sri Ramakrishna College of Arts and Science Coimbatore - 641 006 Tamil Nadu, India 1
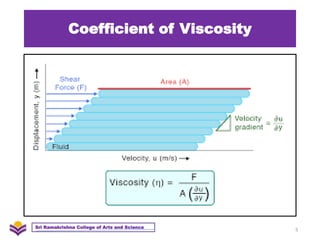
- 2. Coefficient of Viscosity Viscosity: Viscosity is the resistance of a fluid (liquid or gas) to a change in shape or movement of neighboring portions relative to one another. Viscosity denotes opposition to flow. 2 Sri Ramakrishna College of Arts and Science
- 3. Coefficient of Viscosity 3 Sri Ramakrishna College of Arts and Science
- 4. Coefficient of Viscosity The viscosity is calculated in terms of the coefficient of viscosity. It is constant for a liquid and depends on its liquidŌĆÖs nature. The PoiseuilleŌĆÖs method is formally used to estimate the coefficient of viscosity, in which the liquid flows through a tube at the different level of pressures. 4 Sri Ramakrishna College of Arts and Science
- 5. Coefficient of Viscosity 5 Sri Ramakrishna College of Arts and Science
- 6. Streamline Flow Streamline flow in fluids is defined as the flow in which the fluids flow in parallel layers such that there is no disruption or intermixing of the layers and at a given point, the velocity of each fluid particle passing by remains constant with time. (Laminar Flow) In steady (Streamline/Laminar) flow, the density of the fluid remains constant at each point. In unsteady (Turbulent) flow, the velocity of the fluid varies between any given two points. 6 Sri Ramakrishna College of Arts and Science
- 7. Turbulent Flow Turbulent flow is a type of fluid (gas or liquid) flow in which the fluid undergoes irregular fluctuations, or mixing, in contrast to laminar flow, in which the fluid moves in smooth paths or layers. In turbulent flow the speed of the fluid at a point is continuously undergoing changes in both magnitude and direction. 7 Sri Ramakrishna College of Arts and Science
- 8. Streamline & Turbulent Flow 8 Sri Ramakrishna College of Arts and Science
- 9. Critical Velocity & Reynolds number 9 Sri Ramakrishna College of Arts and Science Critical velocity is the speed and direction at which the flow of a liquid through a tube changes from smooth to turbulent. Determining the critical velocity depends on multiple variables, but it is the Reynolds number that characterizes the flow of the liquid through a tube as either turbulent or laminar. The Reynolds number is a dimensionless variable, which means that it has no units attached to it.
- 10. Critical Velocity & Reynolds number 10 Sri Ramakrishna College of Arts and Science Critical Velocity: ØæŻØæÉ = Øæś Ōŗģ Ø£é Ø£īØæ¤ Reynolds number Øæś = ØæŻØæÉØ£īØæ¤ Ōŗģ Ø£é
- 11. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube 11 Sri Ramakrishna College of Arts and Science
- 12. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube Now the velocity of the liquid at a distance Øæ¤ from the axis is ØæŻ and at a distance Øæ¤ + ØææØæ¤ is ØæŻ ŌłÆ ØææØæŻ. So, the velocity gradient=ŌłÆ ØææØæŻ/ØææØæ¤ Surface area of the cylinder, A=2Ø£ŗØæ¤ØæÖ According to NewtonŌĆÖs law viscosity, the viscous Force between two layer is given by ØÉ╣1 = ŌłÆØ£éØÉ┤ØææØæŻ/ØææØæ¤ = ŌłÆØ£é ├Ś 2Ø£ŗØæ¤ØæÖ ├Ś( ØææØæŻ/ØææØæ¤) ----------(1) Where Ø£é= coefficient of viscosity, Now, the forward push due to the difference of pressure P on two sides of the tube of radius r is ØÉ╣2 = Øæā ├Ś ØÉ┤Øæ¤ØæÆØæÄ = Øæā ├Ś Ø£ŗØæ¤2 ---------- (2) 12 Sri Ramakrishna College of Arts and Science
- 13. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube For steady flow, F1= F2 Øæā ├Ś Ø£ŗØæ¤2 = Ø£é ├Ś 2Ø£ŗØæ¤ØæÖ ├Ś( ØææØæŻ/ØææØæ¤) Or ŌģåØÆŚ = ŌłÆØÆæ ؤÉØ£╝ØÆŹ ØÆōØÆģØÆō------------(3) Integrating ŌģåØÆŚ = Ø¤Ä ØÆō ŌłÆØÆæ ؤÉØ£╝ØÆŹ ØÆōØÆģØÆō 13 Sri Ramakrishna College of Arts and Science
- 14. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube ŌģåØÆŚ = Ø¤Ä ØÆō ŌłÆØÆæ ؤÉØ£╝ØÆŹ ØÆōØÆģØÆō ØÆŚ = ŌłÆØÆæØÆōØ¤É Ø¤ÆØ£╝ØÆŹ + Øæ¬ ----- (4) Where r=a & v=0 Ø¤Ä = ŌłÆØÆæØÆéØ¤É Ø¤ÆØ£╝ØÆŹ + Øæ¬ ØÉé = ØÆæØÆéØ¤É Ø¤ÆØ£╝ØÆŹ ØÉé = ØÆæØÆéØ¤É Ø¤ÆØ£╝ØÆŹ ----- (5) Ōł┤ ØÉ» = ØÆæ ؤÆØ£╝ØÆŹ (ØÆéØ¤É ŌłÆ ØÆōؤÉ) ŌĆō (6) 14 Sri Ramakrishna College of Arts and Science
- 15. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube Volume of the liquid flowing per second ØææØæē = ØÉ┤Øæ¤ØæÆØæÄ Øæ£Øæō ØæÉØæ¤Øæ£ØæĀØæĀ ØæåØæÆØæÉØæĪØæ¢Øæ£Øæø Øæ£Øæō ØæĪŌäÄØæÆ ØæĀŌäÄØæÆØæÖØæÖ Øæ£Øæō Øæ¤ØæÄØææØæ¢ØæóØæĀ Øæ¤ ØæÄØæøØææ ØæĪŌäÄØæ¢ØæÉØæśØæÆØæøØæÆØæĀØæĀ ØææØæ¤ ├Ś ØæēØæÆØæÖØæ£ØæÉØæ¢ØæĪØæ” Øæ£Øæō ØæÖØæ£Øæż ØææØæē = 2Ø£ŗØæ¤ØææØæ¤ ØæØ 4Ø£éØæÖ (ØæÄ2 ŌłÆ Øæ¤2) = Ø£ŗØæØ 2Ø£éØæÖ (ØæÄ2Øæ¤ ŌłÆ Øæ¤3) ØææØæ¤ Øæē = 0 ØæÄ Ø£ŗØæØ 2Ø£éØæÖ (ØæÄ2Øæ¤ ŌłÆ Øæ¤3) ØææØæ¤ = Ø£ŗØæØ 2Ø£éØæÖ ØæÄ2 Øæ¤2 2 ŌłÆ Øæ¤4 4 0 ØæÄ 15 Sri Ramakrishna College of Arts and Science
- 16. PoiseuilleŌĆÖs formula for the flow of liquid through a capillary tube Øæē = Ø£ŗØæØ 2Ø£éØæÖ ØæÄ2 Øæ¤2 2 ŌłÆ Øæ¤4 4 0 ØæÄ = Ø£ŗØæØ 2Ø£éØæÖ ØæÄ4 4 Øæē = Ø£ŗØæØØæÄ4 8Ø£éØæÖ 16 Sri Ramakrishna College of Arts and Science
- 17. Corrections to PoiseuilleŌĆÖs Formula Correction for pressure head: Less Effective pressure due to KE acquired ØæØ1 = ØæØ ŌłÆ Øæē2 Ø£ī Ø£ŗ2ØæÄ4 The KE ØÉĖŌĆ▓ = 0 ØæÄ 1 2 2Ø£ŗØææØæ¤ØæŻØ£ī ØæŻ2 = Ø£ŗØ£ī 0 ØæÄ Øæ¤ØæŻ3 ØææØæ¤ But ØæŻ = ØÆæ ؤÆØ£╝ØÆŹ (ØÆéØ¤É ŌłÆ ØÆōؤÉ) Ōł┤ ØÉĖŌĆ▓= Ø£ŗØ£ī 0 ØæÄ Øæ¤ ØÆæ ؤÆØ£╝ØÆŹ 3 (ØÆéØ¤É ŌłÆ ØÆōؤÉ)3ØææØæ¤ 17 Sri Ramakrishna College of Arts and Science
- 18. Corrections to PoiseuilleŌĆÖs Formula ØÉĖŌĆ▓ = Ø£ŗØ£ī ØÆæ ؤÆØ£╝ØÆŹ 3 ØæÄ8 8 = Ø£ŗØæØØæÄ4 8Ø£éØæÖ Ø£ī Ø£ŗ2ØæÄ4 ØÉĖŌĆ▓ = Øæē3 Ø£ī Ø£ŗ2ØæÄ4 Correction for pressure head: ØÉ®ØÉĢ = ØɮؤÅØÉĢ + Øæē3Ø£ī Ø£ŗ2ØæÄ4 Less Effective pressure due to KE acquired ØÆæؤŠ= ØÆæ ŌłÆ ØæĮØ¤É ØØå ØØģؤÉØÆéØ¤Æ = ØÆłØØå ØÆē ŌłÆ ØæĮØ¤É ØØģؤÉØÆéؤÆØÆł 18 Sri Ramakrishna College of Arts and Science
- 19. Corrections to PoiseuilleŌĆÖs Formula Correction for length of the tube: Not streamlined flow for some distance Effective length is increased from ØæÖ ØæĪØæ£ ØæÖ + 1.64ØæÄ. Ø£é = Ø£ŗØæØØæÄ4 8ØæēØæÖ Ø£╝ = ØØģØÆéØ¤Æ Ø¤¢ØæĮ(ØÆŹ + ؤÅ. ؤöؤÆØÆé) ØÆē ŌłÆ ØæĮØ¤É ØØģؤÉØÆéؤÆØÆł ØÆłØØå 19 Sri Ramakrishna College of Arts and Science
- 20. Terminal Velocity The uniform velocity acquired by a body while moving through a highly viscous liquid is called terminal velocity. F = k ØæŻØæÄØæ¤ØæÅØ£éØæÉr F = MLT-2; ØæŻ=LT-1; Øæ¤=L; Ø£é=ML-1T-1; 20 Sri Ramakrishna College of Arts and Science
- 21. StokeŌĆÖs Formula MLT-2=(LT-1)a (L)b (ML-1T-1)c MLT-2=Mc La+b-c T-a-c C = 1 ; a+b+c = 1; -a-c=-2 F=kØæŻØæ¤Ø£é; Øæś = 6Ø£ŗ F= 6Ø£ŗØæŻrØ£é; 21 Sri Ramakrishna College of Arts and Science
- 22. Expression for Terminal Velocity Weight of the ball = 4 3 Ø£ŗØæ¤3Ø£īØæö Weight of the displaced liquid = 4 3 Ø£ŗØæ¤3Ø£īŌĆ▓Øæö Apparent weight of the ball = 4 3 Ø£ŗØæ¤3Ø£īØæö- 4 3 Ø£ŗØæ¤3Ø£īŌĆ▓Øæö = 4 3 Ø£ŗØæ¤3(Ø£ī ŌłÆ Ø£īŌĆ▓)Øæö When the ball attains its terminal velocity, 6Ø£ŗØæŻrØ£é= 4 3 Ø£ŗØæ¤3(Ø£ī ŌłÆ Ø£īŌĆ▓)Øæö ØæŻ = 2 9 Øæ¤2 Ø£é (Ø£ī ŌłÆ Ø£īŌĆ▓)Øæö 22 Sri Ramakrishna College of Arts and Science
- 23. Assumptions made by Stoke ’ā╝ The medium through which the body falls is infinite in extent ’ā╝ The moving body is perfectly rigid and smooth ’ā╝ There is no slip between the moving body and the medium ’ā╝ There are no eddy current or waves set up. The object moves very slowly in the medium 23 Sri Ramakrishna College of Arts and Science
- 24. StokeŌĆÖs Method Terminal velocity ØæŻ = Øæź ØæĪ Coefficient of Viscosity Ø£é = 2 9 Øæ¤2 ØæŻ (Ø£ī ŌłÆ Ø£īŌĆ▓)Øæö 24 Sri Ramakrishna College of Arts and Science
- 25. SearleŌĆÖs Viscometer: Rotating Cylinder Method Angular velocity = Žē Linear velocity = v = r Žē Velocity Gradient = ØææØæŻ ØææØæ¤ = Øææ ØææØæ¤ Øæ¤Ø£ö = Ø£ö ØææØæ¤ ØææØæ¤ + Øæ¤ ØææØ£ö ØææØæ¤ =Ø£ö + Øæ¤ ØææØ£ö ØææØæ¤ 25 Sri Ramakrishna College of Arts and Science
- 26. SearleŌĆÖs Viscometer: Rotating Cylinder Method Since Ø£ö is necessary for preventing slip of a layer, this is not involved in viscous drag. Hence the effective Velocity Gradient =Øæ¤ ØææØ£ö ØææØæ¤ According to newtons formula, F = ╬ĘØÉ┤ ØææØæŻ ØææØæ¤ F = ╬Ę2Ø£ŗØæ¤ØæÖØæ¤ ØææØ£ö ØææØæ¤ Moment of this force = C = ╬Ę2Ø£ŗØæ¤ØæÖØæ¤ ØææØ£ö ØææØæ¤ ├Ś Øæ¤ 26 Sri Ramakrishna College of Arts and Science
- 27. SearleŌĆÖs Viscometer: Rotating Cylinder Method Moment of this force = C = 2Ø£ŗØæÖ╬ĘØæ¤3 ØææØ£ö ØææØæ¤ Øæ£Øæ¤ C ØææØæ¤ Øæ¤3 = 2Ø£ŗØæÖ╬ĘØææØ£ö C ØæÅ ØæÄ ØææØæ¤ Øæ¤3 = 2Ø£ŗØæÖ╬Ę 0 Ø£ö1 ØææØ£ö C ŌłÆ 1 2Øæ¤2 ØæÅ ØæÄ = 2Ø£ŗØæÖ╬ĘØ£ö1 C 2 1 ØæÅ2 ŌłÆ 1 ØæÄ2 ØæÅ ØæÄ = 2Ø£ŗØæÖ╬ĘØ£ö1 ØÉČ = 4Ø£ŗØ£éØ£ö1ØæÄ2ØæÅ2 ØæÄ2 ŌłÆ ØæÅ2 ØæÖ 27 Sri Ramakrishna College of Arts and Science
- 28. SearleŌĆÖs Viscometer: Rotating Cylinder Method 28 Sri Ramakrishna College of Arts and Science