Quarantine Facility Location and Assignment: a Case Study based on the Data of Hong Kong
- 1. Quarantine Facility Location and Assignment: a Case Study based on the Data of Hong Kong TR-GY 7013 Term project Yuhao Liu yl8649@nyu.edu 1
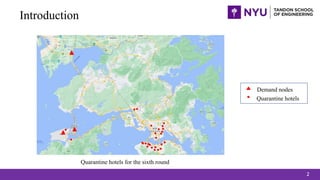
- 2. Demand nodes Quarantine hotels Introduction 2 Quarantine hotels for the sixth round
- 3. System considerations (I) ? Contracting cost ? For each contracted hotel, there is a target revenue guaranteed by the government according to the hotel's profitability. If the actual revenue is less than the target revenue, the government needs to subsidize the hotel by the difference between the target revenue and actual revenue. ? Assignment cost ? In this project, we assume that the cost is merely related to the travel time from the demand nodes to the hotels. ? Risk control ? Ideally, travelers arriving at a same demand node should not be dispersedly assigned to hotels all over the city, so as to contract the range of exposure. 1 0 0 0 1 0 0 0 1 1 1 1 1 1 1 1 1 1 3
- 4. System considerations (II) ? Misplacement ? Travelers have their preference for rooms. Assume that they can report their room preference in advance of the arrivals. To improve that public acceptance of the quarantine policy, the government should try to assign travelers to the rooms that they prefer. However, given the special public health threat, the government has the right to assign a traveler to a room he/she does not prefer. In this case the demand/traveler is said to be misplaced. 4
- 5. 5 Model formulation (I) min min kw kw i iw jk ij i ij jk ij i j k w i j k w kk jk jk ij j k i j k R p Q x c Q Q Q ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??? ???? ?? ??? 1, , , , , , (1 ) , , , , , 0 1, , , , , , {0,1} kw ij i w kw jk ij iw i j k kw ij ik j w k kw ik jk ij ik j kw jk ij jk ij k w k ij i kw ij i ik ij j k Q C x i w y i k C Q y M i k Q Q z i j z N j i j k w x y z ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ?? ?? ? ?? ? ? Subject to
- 6. 1 2 min min kw i ij jk ij i i j k w kw jk ij i j k T c Q Q Z Z ? ? ? ? ? ? ? ???? ??? ( 1) , 0, kw i i iw jk ij i j k w i T R p Q x M i T i ? ? ? ? ? ? ? ? ??? Original constraints Subject to Mixed-integer linear program 6 Model formulation (II) 1 1 2 2 min Z Z ? ? ? Weighting method (”╦1, ”╦2) Subject to all the constraints ? Solved through CPLEX ? Vary (”╦1, ”╦2) to identify non-dominated solutions and construct the pareto frontiers
- 7. Data ? Hong Kong government Covid-19 website ? https://www.coronavirus.gov.hk/eng/ ? Designated Hotels for Quarantine: number and prices of rooms ? Statistics on Passenger Traffic 7 Current: 40 hotels Potential: 48 hotels Demand nodes: 3
- 9. min min kw i ij jk ij i i j k w kk jk ij i j k T c Q Q ? ? ? ? ? ???? ??? 9 Benchmark ? Current locations + optimal assignment 1, , , , , , (1 ) , , , , , kw ij i w kw jk ij iw j k kw ij ik j w k kw ik jk ij ik j kw jk ij jk ij k w k ij i j k Q C i w y i k C Q y M i k Q Q z i j z N j ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ?? ?? ? ?? ? ? 0 1, , , , 0, , , {0,1} kw ij i kw i i iw jk ij j k w ik ij i j k w T i T R p Q i y z ? ? ? ? ? ? ? ? ? ? ? ??? Subject to
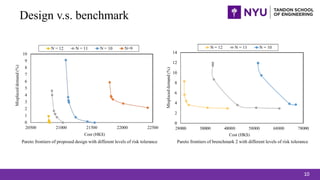
- 10. Design v.s. benchmark 10 Pareto frontiers of proposed design with different levels of risk tolerance Pareto frontiers of brenchmark 2 with different levels of risk tolerance
- 11. Thank you. Merry Christmas! 11