Rail-Fence Cipher Presentation
- 1. The Rail-Fence Cipher Matt Brems Melissa Hannebaum Franklin College
- 3. Methods of Character Encryption Substitution Transposition Plaintext Ciphertext
- 4. Methods of Character Encryption Substitution Plaintext Ciphertext Part Of Key
- 5. Methods of Character Encryption Transposition Plaintext Ciphertext
- 6. Transposition Cipher Columnar A method of encryption in which the plaintext is shifted according to a regular system, so that the ciphertext constitutes a permutation of the plaintext.
- 7. Columnar Transposition As A Function f(x) = y
- 8. Columnar Transposition As A Function Transposition Cipher Plaintext Ciphertext
- 9. Columnar Transposition As A Function The columnar transposition cipher uses a bijective (one-to-one and onto) function to encrypt the text and an inverse function to decrypt the text.
- 10. Columnar Transposition Three Columns C = 3
- 11. Rail-Fence Cipher Two Columns C = 2
- 12. Rail-Fence Cipher C = 2
- 15. Rail-Fence Cipher 4 permutations Conjecture: Length n implies order (n-1)
- 16. Rail-Fence Cipher F R A N K L I N C O L L E G E M A T H A N D C O M P U T I N G ! F A K I C L E E A H N C M U I G R N L N O L G M T A D O P T N ! F K C E A N M I R L O G T D P N A I L E H C U G N N L M A O T ! F C A M R O T P A L H U N L A T K E N I L G D N I E C G N M O ! F A R T A H N A K N L D I C N O C M O P L U L T E I G N E G M ! F R A N K L I N C O L L E G E M A T H A N D C O M P U T I N G !
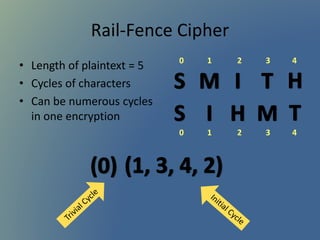
- 17. Rail-Fence Cipher Length of plaintext = 5 Cycles of characters Can be numerous cycles in one encryption 0 1 2 3 4 0 1 2 3 4
- 18. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G ! 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
- 19. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G !
- 20. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G !
- 21. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G !
- 22. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G !
- 23. Length = 16 F R A N K L I N C O L L E G E ! F A K I C L E E R N L N O L G !
- 24. Length Cycle 2 1 3 2 4 2 5 4 6 4 7 3 8 3 9 6, 2 10 6, 2 Length Cycle 11 10 12 10 13 12 14 12 15 4, 2 16 4, 2 32 5 49 21 64 6
- 25. F R A N K L I N C O L L E G E M A T H A N D C O M P U T I N G ! F A K I C L E E A H N C M U I G R N L N O L G M T A D O P T N ! F K C E A N M I R L O G T D P N A I L E H C U G N N L M A O T ! F C A M R O T P A L H U N L A T K E N I L G D N I E C G N M O ! F A R T A H N A K N L D I C N O C M O P L U L T E I G N E G M ! F R A N K L I N C O L L E G E M A T H A N D C O M P U T I N G ! Primes
- 26. General Rules
- 28. Answered Questions What are the fixed points in a RFC? What are the fixed points in a general CTC? Can we tell when the RFC has a k-cycle?
- 29. Unanswered Questions Simple way to calculate length of initial cycle? Can we tell when the CTC has a k-cycle? How much of this works if C > 2?
- 30. Questions?
Editor's Notes
- #11: Column 3 or 4 example like a last name etc Transition to c=2 columnar aka rail fence
- #12: Column 3 or 4 example like a last name etc Transition to c=2 columnar aka rail fence
- #16: Conjecture only on the last slide
- #17: Also only takes 5 (ie conjecture is wrong) How can we know how many? Cycles (answer)
- #18: WHATS GOING ON WITHIN THE FUNCTION???
- #19: N=16
- #25: LENGTH OF 3^n etc and prime factors
- #29: What we accomplished, add patterns Initial length check Fixed points moderate check for RFC Factors PRIMES!! :D REARRANGE