RcppEigen and SVD
- 1. RcppEigen & singular valueRcppEigen & singular value decompositiondecomposition @xiangze750xiangze750 2013/08/312013/08/31 TokyoR#33TokyoR#33 Photo http://www.eigenji-t.jp/admission/Photo http://www.eigenji-t.jp/admission/
- 2. 13/08/31 2 AgendaAgenda ● IntroductionIntroduction ● Eigenvalue problem and SVDEigenvalue problem and SVD ● Examples of SVDExamples of SVD ● How to solve SVDHow to solve SVD ● Randomized SVDRandomized SVD ● EigenEigen ● R and c++R and c++ ● RcppRcpp ● RcppEigenRcppEigen ● RedSVDRedSVD ● ReferencesReferences
- 3. 13/08/31 3 Introduction ● TokyoR#29にて… – Tokyo.R 白熱教室「これからのRcppの話をしよう」 ● http://www.slideshare.net/teramonagi/tokyor-rcpp-16709700 RcppEigenとは、その用途は…?
- 4. 13/08/31 4 Eigenvalue problem &singular value decomposition ● 特異値分解(singular value decomposition)、固 有値問題(Eigenvalue problem ) – 行列を分解する方法 A=U * ΣΣ * V^t A*V=Σ* V (V=U) A 元の行列 ∑ 固有値、特異値行列(非対角要素=0) U,V 行列(各列が特異ベクトル)
- 5. 13/08/31 5 singular value decomposition 特徴的な方向 特 徴 的 な 方 向 ● 固有ベクトル、(左右)特異ベクトル – 線形変換の特徴的な方向を表す行列 ● 固有値、特異値 – 各方向の大きさ A 固有値大 固 有 値 小
- 6. 13/08/31 6 singular value decomposition ● R ではeigen関数、svd関数がある。 – デフォルトではFORTRANで書かれたライ ブラリLAPACKを使用している。 ● Graph用ライブラリigraphでは疎行列用の手法 が利用できる。
- 7. 13/08/31 7 singular value decomposition ● 応用例 – 主成分分析(PCA) (正方行列なので固有値問題) ● 分散共分散行列の主要な方向を固有ベクトルとして抽出する – 自然言語処理におけるLatent Semantic Indexing (LSI, 潜在的 意味インデキシング)http://d.hatena.ne.jp/a_bicky/20100905/1283660172 ● 単語、ドキュメントの頻度行列 – 複雑ネットワークのクラスター抽出(Spectral 法,Pagerank,Newman法) – 画像処理(denoising)、固有顔(Eigenface) 主要な方向 主 要 で な い 方 向
- 8. 13/08/31 8 Examples of SVD ● 複雑ネットワークのクラスター抽出 – Spectral method ● 拡散行列(グラフラプラシアン)の固有値問題 – Pagerank – Newman method ● Modularity Qの近似 ● ● 高次元、疎行列 http://www-stat.stanford.edu/~owen/courses/315c/readings/Padraicsiam_graph_clustering.pdf
- 9. 13/08/31 9 Examples of SVD ● 画像処理(denoising), 固有顔 http://en.wikipedia.org/wiki/Eigenvalues_and_eigenvectors “固有AKB” http://xiangze.hatenablog.com/entry/20111231/1325327854 画像情報 noise
- 10. 13/08/31 10 How to solve SVD ● 直接法(Jacobi法(対象行列のみ)、LR法、QR法) – 行列を三角行列と直交行列に分解→行列要素を対角に近づけ る ● 反復法(Lanczos法, Arnoldi法, Jacobi-Davidson法) – 行列を反復積で三重対角化行列にした後に直接法で解く – 行列の反復積の作る空間=クリロフ部分空間 ● Randomized(乱択)法 – ランダム行列をかけることで行列要素を乱択し、小さな行列 に圧縮する – 近似的な方法
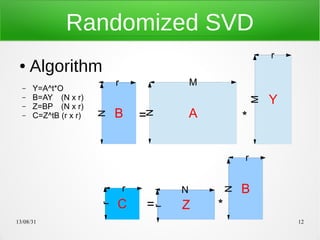
- 11. 13/08/31 11 Randomized SVD ● Algorithm – 入力: 疎(Sparse)な行列A(N x M) – Random行列O(N x r),P(r x r) – Y=A^t*O , Yの各列を正規直交化 – B=AY (N x r) – Z=BP (N x r) , Zの各列を正規直交化 – C=Z^tB (r x r) – Cに対してSVD http://hillbig.cocolog-nifty.com/do/2010/08/redsvd-aa59.html http://amath.colorado.edu/faculty/martinss/Talks/2009_NIPS_tutorial.pdf
- 12. 13/08/31 12 Randomized SVD ● Algorithm – Y=A^t*O – B=AY (N x r) – Z=BP (N x r) – C=Z^tB (r x r) A Z B Y C B = = * * r r N r N r r N N M M r
- 13. 13/08/31 13 Randomized SVD ● Pros. & Cons. 直接法 (LU法、QR法) Lanczos法 Jacobi-Davidson法 Randmized法 長所 ?多くの実装がある (LAPACK等)。 ?厳密 ?疎行列に対して高 速(O(N^2)) ?疎行列に対して高 速 ?上位の固有値だけ を得ることができる ?数値的安定性 ?並列化可能 短所 疎行列の処理に時間 がかかる(O(N^3)) 数値的不安定性 小さな行列に対して は誤差が大きい Randomized法はbig dataにおいて有用?
- 14. 13/08/31 14 About Eigen ● http://eigen.tuxfamily.org/index.php ● C++の行列演算ライブラリ ● わかりやすい記述 ● 豊富な固有値問題Solver ● Expression template – C++の機能templatetemplate(型を変数のように用いることができる)を用いる ● http://d.hatena.ne.jp/faith_and_brave/20081003/1223026720 – 一時変数を生成せず高速 (遅延評価の一種)
- 15. 13/08/31 15 About Eigen ● Eigen 3.2 has been released on July 24, 2013. – Since Eigen 3.1, the key new features of this version are: a built-in supernodal sparse LU solver adapted from SuperLU, a rank-revealing sparse QR factorization with numerical column pivoting, a RealQZ factorization, a GeneralizedEigenSolver, and a Ref<> class allowing to write non templated function taking various kind of Eigen dense objects without copies. – This release also includes a few new functions for dense and sparse matrices, built-in COLAMD ordering, support to SuiteSparse QR and Metis, as well as some accuracy and performance improvements.
- 16. 13/08/31 16 The power of Eigen ● Eigen is fast (in some cases) http://eigen.tuxfamily.org/index.php?title=Benchmark 一般的な行列計算ではEigenは他のライブラリより高速
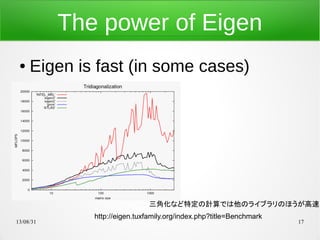
- 17. 13/08/31 17 The power of Eigen ● Eigen is fast (in some cases) http://eigen.tuxfamily.org/index.php?title=Benchmark 三角化など特定の計算では他のライブラリのほうが高速
- 18. 13/08/31 18 R and c++ ● Rで特定の処理を高速化したい場合C++で記述する。 – ここでは固有値問題、SVDに伴う行列計算 ● R – 抽象度が高い、豊富なライブラリ、低速 ● C++ – 高速、コンパイルが必要、むずい(特にメモリ管理)、ライブ ラリもむずい(boost...)
- 19. 13/08/31 19 #include <Rcpp.h> using namespace Rcpp; RcppExport SEXP convolveCpp(SEXP aa,SEXP bb){ NumericVector a(aa); NumericVector b(bb); int na = a.size(), nb = b.size(); int nab = na + nb - 1; NumericVector xab(nab); for (int i = 0; i < na; i++) for (int j = 0; j < nb; j++) xab[i + j] += a[i] * b[j]; return wrap(xab); } Rcpp package ● Rcppはc++で書いたコードとRコードを橋 渡ししてくれるパッケージ 詳しくは”RとC/C++の連携” http://www.slideshare.net/sfchaos/tokyor7rcc A<-c(1,2,3,4) B<-c(5,6,7,8) C<-convolveCpp(A,B) C++ R
- 20. 13/08/31 20 Rcpp package ● Rstudioから簡単コンパイル&実行 – 詳しくはTokyo.RTokyo.R 白熱教室「これからの白熱教室「これからの RcppRcppの話をしよう」の話をしよう」 ● http://www.slideshare.net/teramonagi/tokyor-rcpp-16709700 ● http://www.rstudio.com/ide/docs/advanced/using_rcpp #include <Rcpp.h> using namespace Rcpp; // [[Rcpp::export]]// [[Rcpp::export]] NumericVector convolveCpp(NumericVector a, NumericVector b) { int na = a.size(), nb = b.size(); int nab = na + nb - 1; NumericVector xab(nab); for (int i = 0; i < na; i++) for (int j = 0; j < nb; j++) xab[i + j] += a[i] * b[j]; return xab; }
- 21. 13/08/31 21 RcppEigen ● RcppをつかってC++(Eigen)をwrap ● Features – 入力: as でRのオブジェクトに変換 – 出力: wrapでSEXPに変換 – listを返すこともできる – float型は使用できない Fast and Elegant Numerical Linear Algebra Using the RcppEigen Package http://www.jstatsoft.org/v52/i05/paper
- 22. 13/08/31 22 RcppEigen Fast and Elegant Numerical Linear Algebra Using the RcppEigen Package ● Contents(抜粋) ● 3. Some simple examples – 3.1. Transpose of an integer matrix – 3.2. Products and cross-products – 3.3. Crossproduct of a single matrix – 3.4. Cholesky decomposition of the crossprod ● 4. Least squares solutions ● 5. Delayed evaluation ● 6. Sparse matrices http://www.jstatsoft.org/v52/i05/paper
- 23. 13/08/31 23 RcppEigen ● 記述例 using Eigen::Map; using Eigen::MatrixXd; using Eigen::JacobiSVD; using Rcpp::as; typedef MatrixXd Matd; //d: distance matrix of data //out: output matrix //void mds_eigen(MatrixXf & d,MatrixXf & out){ SEXP mds_rcppeigen(SEXP dd){ const Map<MatrixXd> d(as<Map<MatrixXd> >(dd)); Matd out(Matd(d.rows(),outdim)); Matd d2(d.rows(),d.cols()); Matd nm(d.rows(),d.cols()); d2=d.cwiseProduct(d);//d*d nm.setConstant(-1./d.rows()); nm+=Matd::Identity(nm.rows(),nm.cols()); Matd inm=(nm * d2* nm.transpose())/2; JacobiSVD<MatrixXd> svd(inm, Eigen::ComputeThinU | Eigen::ComputeThinV); MatrixXd sig=svd.singularValues(); MatrixXd u=svd.matrixU(); for(int i=0;i<out.rows();i++) for(int j=0;j<out.cols();j++) out(i,j)=u(i,j)*sqrt(sig(j)); return wrap(out); } Eigen::MapでコピーせずC++(Eigen)コードに渡す
- 24. 13/08/31 24 Randomized SVD ● In R and Eigen 直接法 (LU法、QR法) Lanczos法 Jacobi-Davidson法 Randmized法 R svd, eigen(LAPACK) igraph(ARPACK) なし? Eigen JacobiSVD なし? (ConjugateGradient) RedSVD(external)
- 25. 13/08/31 25 RedSVD ● Randomized SVDのEigen実装 – https://code.google.com/p/redsvd/ ● “例えば,行と列数がそれぞれ10万,非零の要 素が1000万からなる疎行列に対する上位20位 までの特異値分解を約2秒で処理します.” – http://hillbig.cocolog- nifty.com/do/2010/08/redsvd-aa59.html
- 26. 13/08/31 26 Inside RRedSVD ● RRedSVD – Randomized SVDのEigen実装RedSVD のwrapper – https://github.com/xiangze/RRedsvd – 内部は単なるwrapper SEXP redSVDwrap(SEXP AA,SEXP nn){ Rcpp::NumericVector dd(nn); int num=(int)dd[0]; const MappedSparseMatrix<double> A(as<MappedSparseMatrix<double> >(AA)); REDSVD::RedSVD svA(A, num); return List::create(Named("V") = Rcpp::wrap(svA.matrixV()), Named("U")= Rcpp::wrap(svA.matrixU()), Named("D")= Rcpp::wrap(svA.singularValues())); }
- 27. 13/08/31 27 Summary ● C++で高速なアルゴリズムを実装しましょ う。 ● Eigen is fast ● packageを作りましょう
- 28. 13/08/31 28 References ● R & C++ – Tokyo.R 白熱教室「これからのRcppの話をしよう」 ● http://www.slideshare.net/teramonagi/tokyor-rcpp-16709700 – Tokyo.R(#07) RとC++の連携 ● http://www.slideshare.net/sfchaos/tokyor7rcc ● RcppEigen vignette – http://www.jstatsoft.org/v52/i05/paper ● SVD – 今年のSIGKDDベストペーパーを実装?公開してみました(Matrix sketch) ● http://research.preferred.jp/2013/08/sketch/ ● Expression template – Expression Template(式テンプレート)を使って、遅延評価を実現する ● http://d.hatena.ne.jp/teramonagi/20120322/1332428916 – Expression Template ● http://d.hatena.ne.jp/faith_and_brave/20081003/1223026720
- 29. 13/08/31 29 References ● Randomized SVD – "Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions ● http://amath.colorado.edu/faculty/martinss/Talks/2009_NIPS_tutorial.pdf – 行列分解ライブラリredsvdを公開しました ● http://hillbig.cocolog-nifty.com/do/2010/08/redsvd-aa59.html ● https://code.google.com/p/redsvd/ ● Newman-Girvan法のSpectral法による解法 – http://www-stat.stanford.edu/~owen/courses/315c/readings/Padraicsiam_graph_clustering.pdf ● Pseudo-likelihood methods for community detection in large sparse networks – http://research.google.com/pubs/pub40697.html ● 公開コピー誌 行列ライブラリEigenのメモ 暗黒通信団 – http://mikaka.org/~kana/dl/pdf/pdf-eigennote.pdf#search='Eigen+JacobiSVD ● Eigenに似た記述ができるGPGPU向けライブラリArrayFire – http://d.hatena.ne.jp/telmin/20121219/1355929541 ● Gpumatrix A C++ matrix library on GPU with interface compatible with Eigen – https://code.google.com/p/gpumatrix/ ● 固有値問題に対する射影法について(第25回助教の会) – http://jokyos.blogspot.jp/2013/06/blog-post.html ● C++でのLanczos法の実装についてまとめ – http://xiangze.tumblr.com/post/36141657368/lanczos Photo ● 臨済宗永源寺派 大本山 永源寺 http://www.eigenji-t.jp/admission/
















![13/08/31 19
#include <Rcpp.h>
using namespace Rcpp;
RcppExport SEXP convolveCpp(SEXP aa,SEXP bb){
NumericVector a(aa);
NumericVector b(bb);
int na = a.size(), nb = b.size();
int nab = na + nb - 1;
NumericVector xab(nab);
for (int i = 0; i < na; i++)
for (int j = 0; j < nb; j++)
xab[i + j] += a[i] * b[j];
return wrap(xab);
}
Rcpp package
● Rcppはc++で書いたコードとRコードを橋
渡ししてくれるパッケージ
詳しくは”RとC/C++の連携”
http://www.slideshare.net/sfchaos/tokyor7rcc
A<-c(1,2,3,4)
B<-c(5,6,7,8)
C<-convolveCpp(A,B)
C++ R](https://image.slidesharecdn.com/rcppeigenandsvd-130830134704-phpapp01/85/RcppEigen-and-SVD-19-320.jpg)
![13/08/31 20
Rcpp package
● Rstudioから簡単コンパイル&実行
– 詳しくはTokyo.RTokyo.R 白熱教室「これからの白熱教室「これからの
RcppRcppの話をしよう」の話をしよう」
● http://www.slideshare.net/teramonagi/tokyor-rcpp-16709700
● http://www.rstudio.com/ide/docs/advanced/using_rcpp
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]// [[Rcpp::export]]
NumericVector convolveCpp(NumericVector a, NumericVector b) {
int na = a.size(), nb = b.size();
int nab = na + nb - 1;
NumericVector xab(nab);
for (int i = 0; i < na; i++)
for (int j = 0; j < nb; j++)
xab[i + j] += a[i] * b[j];
return xab;
}](https://image.slidesharecdn.com/rcppeigenandsvd-130830134704-phpapp01/85/RcppEigen-and-SVD-20-320.jpg)





![13/08/31 26
Inside RRedSVD
● RRedSVD
– Randomized SVDのEigen実装RedSVD
のwrapper
– https://github.com/xiangze/RRedsvd
– 内部は単なるwrapper
SEXP redSVDwrap(SEXP AA,SEXP nn){
Rcpp::NumericVector dd(nn);
int num=(int)dd[0];
const MappedSparseMatrix<double> A(as<MappedSparseMatrix<double> >(AA));
REDSVD::RedSVD svA(A, num);
return List::create(Named("V") = Rcpp::wrap(svA.matrixV()),
Named("U")= Rcpp::wrap(svA.matrixU()),
Named("D")= Rcpp::wrap(svA.singularValues()));
}](https://image.slidesharecdn.com/rcppeigenandsvd-130830134704-phpapp01/85/RcppEigen-and-SVD-26-320.jpg)


