Recurrence
0 likes4,347 views
This document provides examples of recurrence relations and their solutions. It begins by defining convergence of sequences and limits. It then provides examples of recurrence relations, solving them using algebraic and graphical methods. One example finds the 6th term of a sequence defined by a recurrence relation to be 2.3009. Another example solves a recurrence relation algebraically to express the general term un in terms of n. The document emphasizes using graphical methods like sketching graphs to prove properties of sequences defined by recurrence relations.
1 of 6
Download to read offline

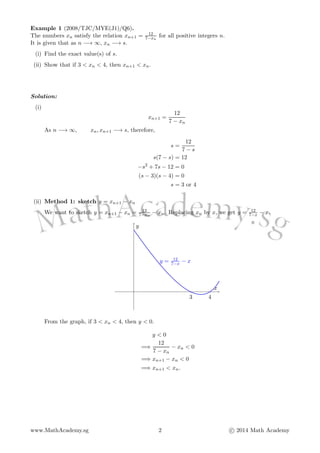
![Example 2 (2011/PJC/II/2 modi´¼üed).
A sequence of positive real numbers x1, x2, x3, . . . satis´¼ües the recurrence relation xn+1 =

3 + xn for
n  1.
(a) If the ´¼ürst term x1 is 1.5, write down the 6th term, that is, x6, leaving your answer to 4 decimal
places.
(b) If the sequence converges to ╬▒, determine the exact value of ╬▒. [2]
(c) By using a graphical method, prove that xn+1 > xn if 0 < x < ╬▒. [2]
(d) Use a calculator to determine the behaviour of the sequence {xn} when x1 = 1. Hence state brie´¼éy
how the results in (c) relate to the behaviour of the sequence. [2]
Solution:
(a) Using GC, x6 = 2.3009.
(b) As n ÔêÆÔåÆ Ôê×, xn, xn+1 ÔêÆÔåÆ ╬▒, therefore,
╬▒ =

3 + ╬▒
╬▒2
= 3 + ╬▒
╬▒2
ÔêÆ ╬▒ ÔêÆ 3 = 0
╬▒ =
1 ┬▒ (ÔêÆ1)2 ÔêÆ 4(1)(ÔêÆ3)
2
=
1 ┬▒

13
2
╬▒ =
1 +

13
2
or
1 

13
2
(rej, since the sequence is positive)
(c) We want to sketch y = xn+1  xn =

3 + xn  xn. Replacing xn by x, we get y =

3 + x  x.
1+

13
2
y =

3 + x  x
x
y
From the graph, if 0 < xn < ╬▒, then y > 0.
y > 0
=

3 + xn  xn > 0
= xn+1  xn > 0
= xn+1 > xn.
(d) Since 0 < x1 < ╬▒, by part (c), xn+1 > xn. Therefore the sequence is strictly increasing. Using
GC, the sequence converges to 2.3028.
www.MathAcademy.sg 4 c 2014 Math Academy](https://image.slidesharecdn.com/recurrence-150423132405-conversion-gate01/85/Recurrence-4-320.jpg)
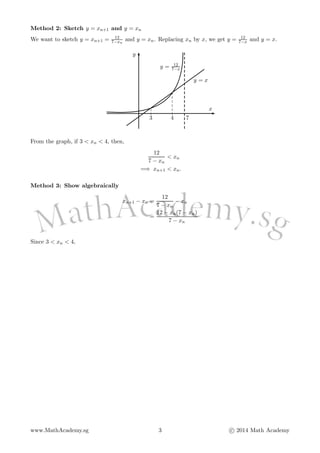
![Example 3.
A sequence of real numbers u1, u2, u3, . . . satis´¼ües the recurrence relation un+1 = 0.9un + 90, a Ôêê R
for all positive integers n and u0 = 1000. Express un in terms n.
Solution:
un = 0.9un1 + 90
= 0.9[0.9un2 + 90] + 90
= 0.92
un2 + 0.9(90) + 90
= 0.92
[0.9un3 + 90] + 0.9(90) + 90
= 0.93
un3 + 0.92
(90) + 0.9(90) + 90
=
...
= 0.9n
u0 + 0.9n1
(90) + 0.9n2
(90) + ┬À ┬À ┬À + 90
= 0.9n
u0 +
90(1  0.9n)
1  0.9
(GP: a = 90, r = 0.9, no. terms = n)
= 0.9n
u0 + 900(1  0.9n
)
= 0.9n
(u0  900) + 900
= 100(0.9n
) + 900 (Since u0 = 1000)
www.MathAcademy.sg 5 c 2014 Math Academy](https://image.slidesharecdn.com/recurrence-150423132405-conversion-gate01/85/Recurrence-5-320.jpg)

Ad
Recommended
Teorema resto y factorNuestra Se├▒ora del Carmen
╠²
El documento describe el teorema del resto y cómo se puede usar para factorizar polinomios cuando la división es exacta, expresando el polinomio como un producto de factores.Teoría de exponentes formularioLeonardo Fabio Guerra Magallanes
╠²
Este documento presenta las teorías básicas de exponentes. 1) Explica que la potencia de una base (An) es igual a la base multiplicada por sí misma n veces. 2) Enumera 13 teorías sobre las operaciones con exponentes, incluyendo que los exponentes de bases iguales se suman, y que elevar una potencia a otra potencia equivale a multiplicar los exponentes. 3) Concluye presentando fórmulas para operar con radicales y exponentes.Higiene En El Deportedavidgalan
╠²
Este documento describe las medidas de higiene y salud que deben seguir los deportistas. Algunas de las principales medidas incluyen dormir al menos 9 horas por d├¡a, ba├▒arse despu├®s de entrenar, lavarse los dientes despu├®s de comer, seguir una dieta equilibrada, y evitar el alcoholismo y el tabaquismo. El documento tambi├®n discute los beneficios de realizar actividad f├¡sica durante la adolescencia, como mejorar los sistemas respiratorio y circulatorio y estimular la formaci├│n de endorfinas.Semana03 ord-2013-iPacoTom14
╠²
Este documento presenta 13 ejercicios de l├│gica matem├ítica y habilidades de razonamiento, junto con sus soluciones. Los ejercicios involucran situaciones como amigos que se sientan en el cine, caballos que compiten en una carrera, y figuras geom├®tricas. El documento provee las respuestas correctas a cada ejercicio.Solucionario PRE SAN MARCOS- Semana 10 Ciclo 2016 Mery Lucy Flores M.
╠²
Este documento presenta 12 ejercicios de matem├íticas con sus respectivas soluciones. Los ejercicios involucran conceptos como progresiones aritm├®ticas, razones, porcentajes y l├│gica. El documento est├í dirigido a estudiantes de un centro preuniversitario en Per├║.Habilidad l├│gico matem├ítica _ semestral _ san marcosJOHANEDSONJULCAMOROQ
╠²
El documento presenta una serie de problemas de l├│gica matem├ítica que abarcan el lanzamiento de dados, el uso de pesas y balanzas, y la distribuci├│n de liquidos en recipientes. Cada problema implica una resoluci├│n donde se busca la soluci├│n ├│ptima en t├®rminos de puntos maximales, trasvases m├¡nimos o pesadas necesarias. Los problemas se encuentran dirigidos a estudiantes que deben aplicar habilidades de razonamiento l├│gico y matem├ítico para encontrar las respuestas correctas.Gu├¡a de octavo ├írea achuradasitayanis
╠²
El documento proporciona una gu├¡a de apoyo de geometr├¡a para octavo b├ísico. Contiene 12 preguntas sobre hallar el ├írea sombreada de diferentes figuras geom├®tricas, con opciones de respuesta para cada pregunta. Tambi├®n incluye la clave de respuestas correctas al final.Ejercicios de Productos NotablesAna Cervantes
╠²
Este documento presenta una serie de ejercicios sobre productos notables que involucran binomios, trinomios y expresiones algebraicas. Los ejercicios cubren temas como calcular cuadrados de binomios, productos de binomios, expresar expresiones en forma de producto, y simplificar expresiones algebraicas usando propiedades de productos notables.Solucion 14Rodolfo Carrillo Velàsquez
╠²
Este documento contiene 14 problemas de trigonometr├¡a resueltos. Los problemas involucran funciones trigonom├®tricas inversas como arcsen, arccos, arcctg y sus relaciones. Se resuelven ecuaciones y expresiones trigonom├®tricas para encontrar valores num├®ricos o rangos de funciones.Division de polinomiosRamiro Mu├▒oz
╠²
Este documento explica el proceso de divisi├│n de polinomios. Primero se ordenan los t├®rminos de mayor a menor exponente. Luego se divide el coeficiente del primer t├®rmino del dividendo entre el coeficiente del primer t├®rmino del divisor. Los t├®rminos literales comunes se restan y los exponentes se llevan al cociente. Este proceso se repite bajando t├®rminos hasta completar la divisi├│n. Se proveen ejemplos para ilustrar los pasos.2010 i semana 16IverSutizal1
╠²
Este documento presenta 14 problemas de matemáticas resueltos. Los problemas cubren temas como rutas, probabilidad, geometría y álgebra. Cada problema viene con una solución detallada. El documento parece ser parte de un solucionario de práctica para un examen de habilidades lógico-matemáticas.Funciones A TrozosAngel Carreras
╠²
Este documento proporciona información sobre funciones a trozos, incluyendo cómo evaluar y graficar este tipo de funciones. Explica que una función a trozos es una combinación de una o más funciones donde la regla cambia en diferentes partes del dominio. Además, presenta ejemplos de cómo evaluar funciones a trozos para diferentes valores de x e incluye instrucciones para graficar funciones a trozos.sequence and series.docx
sequence and series.docxGetachew Mulaw
╠²
The document defines and describes different types of sequences, including arithmetic, harmonic, and geometric sequences. It also discusses the convergence properties of sequences, defining convergent, divergent, and oscillating sequences. Some techniques for evaluating limits of convergent sequences are presented, including using continuous function representations and properties of polynomials.Sequences finding a rule
Sequences finding a ruleDeepak Kumar
╠²
The document discusses sequences, which are sets of terms in a definite order obtained by some rule. It provides examples of finite and infinite sequences and discusses notation for representing sequences. It also covers finding the formula for the terms of a sequence using recurrence relations, which define the initial terms and the relationship between successive terms. The document gives examples of identifying patterns in sequences and finding subsequent terms.Discrete structure sequence, arithmetic progression
Discrete structure sequence, arithmetic progressionharveyspecter1249
╠²
The document is a lecture outline for CSC102 covering discrete structures, specifically focusing on sequences, arithmetic progression, geometric progression, and recurrence relations. It includes definitions, examples, and methods for defining and solving sequences, including the Fibonacci sequence and factorial sequences. Additionally, it discusses techniques for deducing formulas from given terms of sequences.3.-SEQUENCES-AND-SERIES-THEORY.hhsssspdf
3.-SEQUENCES-AND-SERIES-THEORY.hhsssspdfnassorokayanda9412
╠²
This document discusses sequences and series, defining a sequence as an ordered collection of terms, either finite or infinite. It explains how to determine the general term (tn) of a sequence, provides examples, and details the properties of arithmetic progressions (AP) along with rules for calculating terms. Additionally, it introduces sigma and pi notations for summation and product, respectively, along with examples of how to use them in mathematical contexts.Presentation4
Presentation4VocaloidEX
╠²
This document discusses sequences and their properties. It defines sequences and provides examples of different types of sequences including arithmetic, geometric, harmonic, and Fibonacci sequences. It discusses finding formulas for the nth term of sequences and calculating sums of sequence terms. Examples are provided to demonstrate finding sequence terms, recognizing sequence types based on patterns of terms, and using recurrence relations to define sequences.sequenceandseries-150221091317-conversion-gate01.pdf
sequenceandseries-150221091317-conversion-gate01.pdfMuhammadJamil152989
╠²
The document defines sequences and series in mathematics. A sequence is an ordered list of elements where order matters, and can be finite or infinite. Associated with every sequence is a series, which is the sum of the terms of the sequence and can be written using sigma notation.10-Sequences and summation.pptx
10-Sequences and summation.pptxjaffarbikat
╠²
The document discusses sequences and summations. It provides examples and definitions of different types of sequences such as arithmetic and geometric sequences. It also discusses recurrence relations, which express a term in a sequence based on prior terms. Examples are provided to demonstrate finding terms of sequences given a recurrence relation. The document is a lecture on discrete mathematics concepts related to sequences.Chap2
Chap2dinhmyhuyenvi
╠²
This chapter introduces the concept of a limit, which is the most important notion in mathematical analysis. The chapter defines what it means for a sequence of numbers to converge or have a limit. Specifically, it provides the precise definition that the limit L of a sequence {an} is the number such that for any positive number ╬Á, there exists an N where if n ÔëÑ N, the distance between an and L is less than ╬Á. The chapter then gives examples of applying this definition to determine the limits of various sequences. It also defines divergence to positive or negative infinity and discusses properties of limits.Lecture # 20.pptx
Lecture # 20.pptxMussabChodhry
╠²
Here are the steps to solve these problems:
1) Let a = 4 (first term), r = 1/2 (common ratio)
Then the nth term is an = a(r)n-1
Setting an = 1/8, we get:
1/8 = 4(1/2)n-1
1/8 = 2(1/2)n-1
n-1 = 3
n = 4
Therefore, the 4th term is 1/8.
2) Let a = first term, r = common ratio
Given: a2 = 9, a4 = 1
a2 = a(r)
9 = a(r)
Lesson 1a_Sequence.pptx
Lesson 1a_Sequence.pptxBaldonMarcelo1
╠²
The document defines and provides examples of sequences, including infinite sequences and their general terms. It discusses finding the general term of a sequence from its given terms. The document also introduces concepts such as the limit of a sequence, monotone sequences, and bounded sequences. Examples are provided to demonstrate evaluating limits of sequences, determining if a sequence is monotone or strictly monotone, and determining if a sequence is bounded. Exercises are included for readers to practice applying the concepts.AYUSH.pptx
AYUSH.pptxamwebsite12345
╠²
1. The document discusses sequences and series in mathematics. It defines sequences, convergence of sequences, infinite series, and tests to determine convergence of series such as the ratio test, root test, integral test, alternating series test, and absolute and conditional convergence.
2. Examples are provided to illustrate concepts like determining if a sequence converges based on the limit of its terms, and using tests like the ratio test to analyze the convergence of infinite series.
3. Different types of series are discussed including alternating series, and conditions for absolute and conditional convergence are defined.6.sequences and series Further Mathematics Zimbabwe Zimsec Cambridge
6.sequences and series Further Mathematics Zimbabwe Zimsec Cambridgealproelearning
╠²
This document introduces the mathematical technique of proof by induction. It uses the analogy of an inventor testing a climbing robot on ladders of varying lengths to illustrate the two conditions necessary for the robot to climb any ladder: 1) it must be able to reach the first rung, and 2) if it has reached a rung, it must be able to reach the next rung. If the robot satisfies these two conditions, it can climb infinitely high by repeatedly satisfying condition 2 after condition 1. This climbing robot analogy demonstrates how proof by induction works - it proves that a statement is true for all positive integers by showing it is true for the first integer, and then showing that if it is true for any integer n, it mustSequence function
Sequence functionjennytuazon01630
╠²
The document defines key concepts related to sequences and series. It explains that a sequence is an ordered list of numbers with a specific pattern or rule. A sequence function is a function whose domain is the set of natural numbers. Terms are the individual numbers in a sequence. Finite sequences have a set number of terms while infinite sequences continue without end. Partial sums refer to adding a specific number of terms. Sigma notation compactly represents the sum of terms in a sequence. The document also introduces the principle of mathematical induction as a method to prove that statements are true for all natural numbers.Sequence and series
Sequence and seriesDenmar Marasigan
╠²
The document defines sequences and series. A sequence is an ordered list of elements where order matters. Sequences can be finite or infinite. A series is the sum of the terms of a sequence. Sigma notation is used to represent the sum of terms in a sequence from one index to another. Examples show how to write out the terms of a sequence given a general term formula and how to express a series without sigma notation.090799768954
090799768954FERNAN85
╠²
The document provides information about sequences, including defining characteristics, types of sequences, general terms of sequences, recursive and explicit formulas, and examples. It discusses finite and infinite sequences, terms in a sequence, writing the general nth term as a function, and finding specific terms. Examples of sequences include the Fibonacci sequence and using the golden ratio in photography. Worked problems demonstrate finding terms of sequences given their formulas.Mth3101 Advanced Calculus Chapter 2
Mth3101 Advanced Calculus Chapter 2saya efan
╠²
This document defines and provides examples of sequences of real numbers. It begins by defining a sequence as a set of numbers written in a definite order. Examples are provided to illustrate bounded, increasing, decreasing, convergent, and divergent sequences. The limit of a sequence is defined as the number L that the terms of the sequence approach as n becomes large. A sequence is convergent if its limit exists and divergent otherwise. Bounded sequences are those for which the terms are all less than some positive number M, but bounded sequences may still diverge. Recursively defined sequences are also discussed.More Related Content
What's hot (6)
Ejercicios de Productos NotablesAna Cervantes
╠²
Este documento presenta una serie de ejercicios sobre productos notables que involucran binomios, trinomios y expresiones algebraicas. Los ejercicios cubren temas como calcular cuadrados de binomios, productos de binomios, expresar expresiones en forma de producto, y simplificar expresiones algebraicas usando propiedades de productos notables.Solucion 14Rodolfo Carrillo Velàsquez
╠²
Este documento contiene 14 problemas de trigonometr├¡a resueltos. Los problemas involucran funciones trigonom├®tricas inversas como arcsen, arccos, arcctg y sus relaciones. Se resuelven ecuaciones y expresiones trigonom├®tricas para encontrar valores num├®ricos o rangos de funciones.Division de polinomiosRamiro Mu├▒oz
╠²
Este documento explica el proceso de divisi├│n de polinomios. Primero se ordenan los t├®rminos de mayor a menor exponente. Luego se divide el coeficiente del primer t├®rmino del dividendo entre el coeficiente del primer t├®rmino del divisor. Los t├®rminos literales comunes se restan y los exponentes se llevan al cociente. Este proceso se repite bajando t├®rminos hasta completar la divisi├│n. Se proveen ejemplos para ilustrar los pasos.2010 i semana 16IverSutizal1
╠²
Este documento presenta 14 problemas de matemáticas resueltos. Los problemas cubren temas como rutas, probabilidad, geometría y álgebra. Cada problema viene con una solución detallada. El documento parece ser parte de un solucionario de práctica para un examen de habilidades lógico-matemáticas.Funciones A TrozosAngel Carreras
╠²
Este documento proporciona información sobre funciones a trozos, incluyendo cómo evaluar y graficar este tipo de funciones. Explica que una función a trozos es una combinación de una o más funciones donde la regla cambia en diferentes partes del dominio. Además, presenta ejemplos de cómo evaluar funciones a trozos para diferentes valores de x e incluye instrucciones para graficar funciones a trozos.Similar to Recurrence (20)
sequence and series.docx
sequence and series.docxGetachew Mulaw
╠²
The document defines and describes different types of sequences, including arithmetic, harmonic, and geometric sequences. It also discusses the convergence properties of sequences, defining convergent, divergent, and oscillating sequences. Some techniques for evaluating limits of convergent sequences are presented, including using continuous function representations and properties of polynomials.Sequences finding a rule
Sequences finding a ruleDeepak Kumar
╠²
The document discusses sequences, which are sets of terms in a definite order obtained by some rule. It provides examples of finite and infinite sequences and discusses notation for representing sequences. It also covers finding the formula for the terms of a sequence using recurrence relations, which define the initial terms and the relationship between successive terms. The document gives examples of identifying patterns in sequences and finding subsequent terms.Discrete structure sequence, arithmetic progression
Discrete structure sequence, arithmetic progressionharveyspecter1249
╠²
The document is a lecture outline for CSC102 covering discrete structures, specifically focusing on sequences, arithmetic progression, geometric progression, and recurrence relations. It includes definitions, examples, and methods for defining and solving sequences, including the Fibonacci sequence and factorial sequences. Additionally, it discusses techniques for deducing formulas from given terms of sequences.3.-SEQUENCES-AND-SERIES-THEORY.hhsssspdf
3.-SEQUENCES-AND-SERIES-THEORY.hhsssspdfnassorokayanda9412
╠²
This document discusses sequences and series, defining a sequence as an ordered collection of terms, either finite or infinite. It explains how to determine the general term (tn) of a sequence, provides examples, and details the properties of arithmetic progressions (AP) along with rules for calculating terms. Additionally, it introduces sigma and pi notations for summation and product, respectively, along with examples of how to use them in mathematical contexts.Presentation4
Presentation4VocaloidEX
╠²
This document discusses sequences and their properties. It defines sequences and provides examples of different types of sequences including arithmetic, geometric, harmonic, and Fibonacci sequences. It discusses finding formulas for the nth term of sequences and calculating sums of sequence terms. Examples are provided to demonstrate finding sequence terms, recognizing sequence types based on patterns of terms, and using recurrence relations to define sequences.sequenceandseries-150221091317-conversion-gate01.pdf
sequenceandseries-150221091317-conversion-gate01.pdfMuhammadJamil152989
╠²
The document defines sequences and series in mathematics. A sequence is an ordered list of elements where order matters, and can be finite or infinite. Associated with every sequence is a series, which is the sum of the terms of the sequence and can be written using sigma notation.10-Sequences and summation.pptx
10-Sequences and summation.pptxjaffarbikat
╠²
The document discusses sequences and summations. It provides examples and definitions of different types of sequences such as arithmetic and geometric sequences. It also discusses recurrence relations, which express a term in a sequence based on prior terms. Examples are provided to demonstrate finding terms of sequences given a recurrence relation. The document is a lecture on discrete mathematics concepts related to sequences.Chap2
Chap2dinhmyhuyenvi
╠²
This chapter introduces the concept of a limit, which is the most important notion in mathematical analysis. The chapter defines what it means for a sequence of numbers to converge or have a limit. Specifically, it provides the precise definition that the limit L of a sequence {an} is the number such that for any positive number ╬Á, there exists an N where if n ÔëÑ N, the distance between an and L is less than ╬Á. The chapter then gives examples of applying this definition to determine the limits of various sequences. It also defines divergence to positive or negative infinity and discusses properties of limits.Lecture # 20.pptx
Lecture # 20.pptxMussabChodhry
╠²
Here are the steps to solve these problems:
1) Let a = 4 (first term), r = 1/2 (common ratio)
Then the nth term is an = a(r)n-1
Setting an = 1/8, we get:
1/8 = 4(1/2)n-1
1/8 = 2(1/2)n-1
n-1 = 3
n = 4
Therefore, the 4th term is 1/8.
2) Let a = first term, r = common ratio
Given: a2 = 9, a4 = 1
a2 = a(r)
9 = a(r)
Lesson 1a_Sequence.pptx
Lesson 1a_Sequence.pptxBaldonMarcelo1
╠²
The document defines and provides examples of sequences, including infinite sequences and their general terms. It discusses finding the general term of a sequence from its given terms. The document also introduces concepts such as the limit of a sequence, monotone sequences, and bounded sequences. Examples are provided to demonstrate evaluating limits of sequences, determining if a sequence is monotone or strictly monotone, and determining if a sequence is bounded. Exercises are included for readers to practice applying the concepts.AYUSH.pptx
AYUSH.pptxamwebsite12345
╠²
1. The document discusses sequences and series in mathematics. It defines sequences, convergence of sequences, infinite series, and tests to determine convergence of series such as the ratio test, root test, integral test, alternating series test, and absolute and conditional convergence.
2. Examples are provided to illustrate concepts like determining if a sequence converges based on the limit of its terms, and using tests like the ratio test to analyze the convergence of infinite series.
3. Different types of series are discussed including alternating series, and conditions for absolute and conditional convergence are defined.6.sequences and series Further Mathematics Zimbabwe Zimsec Cambridge
6.sequences and series Further Mathematics Zimbabwe Zimsec Cambridgealproelearning
╠²
This document introduces the mathematical technique of proof by induction. It uses the analogy of an inventor testing a climbing robot on ladders of varying lengths to illustrate the two conditions necessary for the robot to climb any ladder: 1) it must be able to reach the first rung, and 2) if it has reached a rung, it must be able to reach the next rung. If the robot satisfies these two conditions, it can climb infinitely high by repeatedly satisfying condition 2 after condition 1. This climbing robot analogy demonstrates how proof by induction works - it proves that a statement is true for all positive integers by showing it is true for the first integer, and then showing that if it is true for any integer n, it mustSequence function
Sequence functionjennytuazon01630
╠²
The document defines key concepts related to sequences and series. It explains that a sequence is an ordered list of numbers with a specific pattern or rule. A sequence function is a function whose domain is the set of natural numbers. Terms are the individual numbers in a sequence. Finite sequences have a set number of terms while infinite sequences continue without end. Partial sums refer to adding a specific number of terms. Sigma notation compactly represents the sum of terms in a sequence. The document also introduces the principle of mathematical induction as a method to prove that statements are true for all natural numbers.Sequence and series
Sequence and seriesDenmar Marasigan
╠²
The document defines sequences and series. A sequence is an ordered list of elements where order matters. Sequences can be finite or infinite. A series is the sum of the terms of a sequence. Sigma notation is used to represent the sum of terms in a sequence from one index to another. Examples show how to write out the terms of a sequence given a general term formula and how to express a series without sigma notation.090799768954
090799768954FERNAN85
╠²
The document provides information about sequences, including defining characteristics, types of sequences, general terms of sequences, recursive and explicit formulas, and examples. It discusses finite and infinite sequences, terms in a sequence, writing the general nth term as a function, and finding specific terms. Examples of sequences include the Fibonacci sequence and using the golden ratio in photography. Worked problems demonstrate finding terms of sequences given their formulas.Mth3101 Advanced Calculus Chapter 2
Mth3101 Advanced Calculus Chapter 2saya efan
╠²
This document defines and provides examples of sequences of real numbers. It begins by defining a sequence as a set of numbers written in a definite order. Examples are provided to illustrate bounded, increasing, decreasing, convergent, and divergent sequences. The limit of a sequence is defined as the number L that the terms of the sequence approach as n becomes large. A sequence is convergent if its limit exists and divergent otherwise. Bounded sequences are those for which the terms are all less than some positive number M, but bounded sequences may still diverge. Recursively defined sequences are also discussed.series.pdf
series.pdfJorge Vega Rodríguez
╠²
This document provides an overview of sequences and series. It defines what a sequence is, discusses concepts like convergence and divergence of sequences, and introduces common types of sequences like an = n and an = 1/n. It also presents rules for determining limits of sequences, such as the sum and product rules. Examples are provided to demonstrate applying these rules and the squeeze theorem for limits.Sequences_Arithmetic_Harmonic_Geometric.ppt
Sequences_Arithmetic_Harmonic_Geometric.pptsrei8348
╠²
This document explains arithmetic and geometric sequences and their properties. It covers how to identify terms, find the common difference or ratio, and compute terms using specific formulas. Additionally, it provides examples illustrating how to derive terms and the rules governing these sequences.Chapter 1 sequences and series
Chapter 1 sequences and serieswan suriyani che wan ahmad
╠²
The document discusses sequences and series, including arithmetic and geometric sequences and series. It provides examples and formulas to find terms of sequences and the sums of finite and infinite series. It also gives exercises with solutions to apply these concepts, such as finding specific terms, determining sums, and solving application problems involving sequences and series.Section 11.1
Section 11.1 CalculusII
╠²
The document provides an overview of sequences and the limit of a sequence. It defines an infinite sequence as a list of numbers in a definite order, with an denoting the nth term. The limit of a sequence is the number L such that the terms an can be made arbitrarily close to L by taking a sufficiently large n. Several properties of convergent sequences are described, including limit laws and the squeeze theorem. Special types of divergence like divergence to infinity are also covered. Examples are provided to illustrate key concepts.Ad
More from Math Academy Singapore (14)
Sec 3 A Maths Notes Indices
Sec 3 A Maths Notes IndicesMath Academy Singapore
╠²
1. The document discusses solving exponential equations with one, two, or three terms using properties of exponents such as changing bases to the same term and equating powers.
2. Examples are provided for solving two-term exponential equations by making the bases equal and equations with three terms by substituting variables, changing bases to the same term, and equating powers.
3. Solving exponential equations as products using properties such as treating exponents as multipliers is also demonstrated through examples.Sec 4 A Maths Notes Maxima Minima
Sec 4 A Maths Notes Maxima MinimaMath Academy Singapore
╠²
The document contains two examples of maximum and minimum problems involving differentiation.
Example 1 asks the reader to find the minimum volume of a cone given that a sphere must fit inside it. It is found that the minimum volume occurs when the radius of the cone is 28.577 cm.
Example 2 involves finding the maximum volume of a cylinder inscribed in a sphere. The maximum volume is calculated to be 104,000 cm3, occurring when the height of the cylinder is 28.5 cm.
The document provides guidance on solving maximum and minimum problems using differentiation, illustrated through these two examples involving geometric shapes.Sec 3 E Maths Notes Coordinate Geometry
Sec 3 E Maths Notes Coordinate GeometryMath Academy Singapore
╠²
This document provides examples and explanations of using the distance formula and equations of lines in coordinate geometry. It defines the distance formula and shows how to calculate the distance between two points with given coordinates. It also demonstrates how to determine the gradient and y-intercept of a line given its equation, find the equation of a line given the gradient and a point or two points, and find values related to lines parallel or intersecting given lines.Sec 3 A Maths Notes Indices
Sec 3 A Maths Notes IndicesMath Academy Singapore
╠²
1) The document provides examples of solving exponential equations with various methods depending on whether the equation has two terms, three or more terms, or involves indices as products or quotients.
2) Key steps include splitting equations, letting one term equal a variable, raising both sides to the same power, and changing all terms to have the same base before equating exponents.
3) Examples range from simple equations like 82=x to more complex ones involving subtraction, addition, and multiplication of terms with different bases and exponents like (23)3=x+2-x.Sec 2 Maths Notes Change Subject
Sec 2 Maths Notes Change SubjectMath Academy Singapore
╠²
The document provides examples and techniques for changing the subject of a formula. It demonstrates flipping both sides of an equation, multiplying or dividing both sides by the same term, and isolating the term to be made the subject by collecting like terms on one side of the equation and leaving the term by itself on the other side. Common mistakes discussed include incorrectly flipping terms individually rather than both sides of the equation and prematurely making denominators the same.Sec 1 Maths Notes Equations
Sec 1 Maths Notes EquationsMath Academy Singapore
╠²
1) The document provides steps for solving simple linear equations with no fractions and fractional equations.
2) For linear equations with no fractions, the steps are to expand if there is a bracket, group like terms to one side, and then solve for the variable.
3) For fractional equations, the steps are to multiply both sides by the common denominator to clear the fractions, then group like terms and solve.JC Vectors summary
JC Vectors summaryMath Academy Singapore
╠²
1. The document provides revision on various topics in vectors including ratio theorem, scalar and vector products, lines, planes, perpendiculars, reflections, angles, distances, direction cosines, and geometric meanings.
2. Key concepts covered include using scalar and vector products to find angles between lines, planes, and determining if lines or planes are parallel/perpendicular.
3. Methods for finding the foot of a perpendicular from a point to a line or plane, reflecting lines and planes, and determining relationships between lines and planes are summarized.Functions JC H2 Maths
Functions JC H2 MathsMath Academy Singapore
╠²
This document defines functions and their key properties such as domain, range, and inverse functions. It provides examples of determining whether a function is one-to-one and finding its inverse. Composite functions are discussed, including ensuring the range of the inner function is contained within the domain of the outer function. Self-inverse functions are introduced, where the inverse of a function is equal to the function itself.Vectors2
Vectors2Math Academy Singapore
╠²
The document discusses various topics related to vectors and planes:
1. It explains the vector product in three forms - mathematical calculation, 3D picture, and in terms of sine. It provides an example to calculate the vector product of two vectors.
2. It discusses the different forms of the equation of a plane - parametric, scalar product, and Cartesian forms. It provides examples to write the equation of a plane in these different forms.
3. It explains how to find the foot of the perpendicular from a point to a plane. It provides examples to find the foot and shortest distance.
4. It discusses how to find acute angles between lines, planes, and a line and plane. ExamplesMath academy-partial-fractions-notes
Math academy-partial-fractions-notesMath Academy Singapore
╠²
This document provides an introduction to partial fractions. It defines key terms like polynomials, rational functions, and proper and improper fractions. It then outlines the three main cases for splitting a fraction into partial fractions: (1) a linear factor (ax+b), (2) a repeated linear factor, and (3) a quadratic factor (ax^2+bx+c). For each case, it provides an example of how to write the fraction as a sum of partial fractions. It concludes by emphasizing two important checks: (1) the fraction must be proper, and (2) the denominator must be completely factorized before attempting to write it as partial fractions.Complex Numbers 1 - Math Academy - JC H2 maths A levels
Complex Numbers 1 - Math Academy - JC H2 maths A levelsMath Academy Singapore
╠²
The document provides lessons on complex numbers. It defines a complex number as being of the form z = x + iy, where x and y are real numbers. It discusses operations like addition, subtraction, multiplication and division of complex numbers. It also defines the complex conjugate and gives some examples of performing operations on complex numbers.Functions 1 - Math Academy - JC H2 maths A levels
Functions 1 - Math Academy - JC H2 maths A levelsMath Academy Singapore
╠²
This document covers the concepts of functions, including their definition, domain, range, and characteristics such as 1-1 functions and the horizontal line test. It provides various examples to illustrate how to find the range of functions and determine whether they are 1-1 by analyzing their graphs and derivatives. Additionally, the document discusses inverse functions, their properties, and the relationship between a function and its inverse.Probability 2 - Math Academy - JC H2 maths A levels
Probability 2 - Math Academy - JC H2 maths A levelsMath Academy Singapore
╠²
The document provides information on probability concepts including Venn diagrams, union and intersection of events, useful probability formulas, mutually exclusive vs independent events, and examples testing these concepts. Specifically, it defines union as "taking everything in A and B", intersection as "taking common parts in A and B", provides formulas for probability of unions and intersections, and shows how to determine if events are mutually exclusive or independent using the probability of their intersection. It also includes worked examples testing concepts like mutually exclusive events and independence.Probability 1 - Math Academy - JC H2 maths A levels
Probability 1 - Math Academy - JC H2 maths A levelsMath Academy Singapore
╠²
The document discusses conditional probability and provides examples. It defines conditional probability P(A|B) as the probability of event A occurring given that event B has already occurred. An example calculates probabilities for drawing marbles from a bag. Another example finds probabilities for selecting chocolates with different flavors from a box containing chocolates of various flavors. Formulas and step-by-step workings are provided for calculating conditional probabilities.Ad
Recently uploaded (20)
How to Manage Different Customer Addresses in Odoo 18 Accounting
How to Manage Different Customer Addresses in Odoo 18 AccountingCeline George
╠²
A business often have customers with multiple locations such as office, warehouse, home addresses and this feature allows us to associate with different addresses with each customer streamlining the process of creating sales order invoices and delivery orders.M&A5 Q1 1 differentiate evolving early Philippine conventional and contempora...
M&A5 Q1 1 differentiate evolving early Philippine conventional and contempora...ErlizaRosete
╠²
MAPEH 6 QI WEEK IECONOMICS, DISASTER MANAGEMENT, ROAD SAFETY - STUDY MATERIAL [10TH]
ECONOMICS, DISASTER MANAGEMENT, ROAD SAFETY - STUDY MATERIAL [10TH]SHERAZ AHMAD LONE
╠²
This study material for Class 10th covers the core subjects of Economics, Disaster Management, and Road Safety Education, developed strictly in line with the JKBOSE textbook. It presents the content in a simplified, structured, and student-friendly format, ensuring clarity in concepts. The material includes reframed explanations, flowcharts, infographics, and key point summaries to support better understanding and retention. Designed for classroom teaching and exam preparation, it aims to enhance comprehension, critical thinking, and practical awareness among students.Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powelltrjnesjnqg7801
╠²
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane PowellINDUCTIVE EFFECT slide for first prof pharamacy students
INDUCTIVE EFFECT slide for first prof pharamacy studentsSHABNAM FAIZ
╠²
The inductive effect is the electron-withdrawing or electron-donating effect transmitted through sigma (¤â) bonds in a molecule due to differences in electronegativity between atoms.
---
ƒö╣ Definition:
The inductive effect is the permanent shifting of electrons in a sigma bond caused by the electronegativity difference of atoms, resulting in partial charges within the molecule.University of Ghana Cracks Down on Misconduct: Over 100 Students Sanctioned
University of Ghana Cracks Down on Misconduct: Over 100 Students SanctionedKweku Zurek
╠²
University of Ghana Cracks Down on Misconduct: Over 100 Students Sanctioned
June 2025 Progress Update With Board Call_In process.pptx
June 2025 Progress Update With Board Call_In process.pptxInternational Society of Service Innovation Professionals
╠²
---
June 25 ISSIP Event - slides in process
20250618 PPre-Event Presentation Summary - Progress Update with Board Series June 25
ISSIP Website Upcoming Events Description: https://issip.org/event/semi-annual-issip-progress-call/
Register here (even if you cannot attend live online, all who register will get link to recording and slides post-event): https://docs.google.com/forms/d/e/1FAIpQLSdThrop1rafOCo4PQkYiS2XApclJuMjYONEHRMGBsceRdcQqg/viewform
This pre-event presentation: /slideshow/june-2025-progress-update-with-board-call_in-process-pptx/280718770
This pre-event recording: https://youtu.be/Shjgd5o488o
---Tanja Vujicic - PISA for Schools contact Info
Tanja Vujicic - PISA for Schools contact InfoEduSkills OECD
╠²
Tanja Vujicic, Senior Analyst and PISA for SchoolÔÇÖs Project Manager at the OECD spoke at the OECD webinar 'Turning insights into impact: What do early case studies reveal about the power of PISA for Schools?' on 20 June 2025
PISA for Schools is an OECD assessment that evaluates 15-year-old performance on reading, mathematics, and science. It also gathers insights into studentsÔÇÖ learning environment, engagement and well-being, offering schools valuable data that help them benchmark performance internationally and improve education outcomes. A central ambition, and ongoing challenge, has been translating these insights into meaningful actions that drives lasting school improvement. This is why students from these 44 institutions have not received National Se...
This is why students from these 44 institutions have not received National Se...Kweku Zurek
╠²
This is why students from these 44 institutions have not received National Service PIN codes (LIST)How payment terms are configured in Odoo 18
How payment terms are configured in Odoo 18Celine George
╠²
Payment terms in Odoo 18 help define the conditions for when invoices are due. This feature can split payments into multiple parts and automate due dates based on specific rules.Code Profiling in Odoo 18 - Odoo 18 ║¦║¦▀ús
Code Profiling in Odoo 18 - Odoo 18 ║¦║¦▀úsCeline George
╠²
Profiling in Odoo identifies slow code and resource-heavy processes, ensuring better system performance. Odoo code profiling detects bottlenecks in custom modules, making it easier to improve speed and scalability.OBSESSIVE COMPULSIVE DISORDER.pptx IN 5TH SEMESTER B.SC NURSING, 2ND YEAR GNM...
OBSESSIVE COMPULSIVE DISORDER.pptx IN 5TH SEMESTER B.SC NURSING, 2ND YEAR GNM...parmarjuli1412
╠²
OBSESSIVE COMPULSIVE DISORDER INCLUDED TOPICS ARE INTRODUCTION, DEFINITION OF OBSESSION, DEFINITION OF COMPULSION, MEANING OF OBSESSION AND COMPULSION, DEFINITION OF OBSESSIVE COMPULSIVE DISORDER, EPIDERMIOLOGY OF OCD, ETIOLOGICAL FACTORS OF OCD, CLINICAL SIGN AND SYMPTOMS OF OBSESSION AND COMPULSION, MANAGEMENT INCLUDED PHARMACOTHERAPY(ANTIDEPRESSANT DRUG+ANXIOLYTIC DRUGS), PSYCHOTHERAPY, NURSING MANAGEMENT(ASSESSMENT+DIAGNOSIS+NURSING INTERVENTION+EVALUATION)) HistoPathology Ppt. Arshita Gupta for Diploma
HistoPathology Ppt. Arshita Gupta for Diplomaarshitagupta674
╠²
Hello everyone please suggest your views and likes so that I uploaded more study materials
In this slide full HistoPathology according to diploma course available like fixation
Tissue processing , staining etc
Aprendendo Arquitetura Framework Salesforce - Dia 02
Aprendendo Arquitetura Framework Salesforce - Dia 02Mauricio Alexandre Silva
╠²
Aprendendo Arquitetura Framework Salesforce - Dia 02
SCHIZOPHRENIA OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndr...
SCHIZOPHRENIA OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndr...parmarjuli1412
╠²
SCHIZOPHRENIA INCLUDED TOPIC IS INTRODUCTION, DEFINITION OF GENERAL TERM IN PSYCHIATRIC, THEN DIFINITION OF SCHIZOPHRENIA, EPIDERMIOLOGY, ETIOLOGICAL FACTORS, CLINICAL FEATURE(SIGN AND SYMPTOMS OF SCHIZOPHRENIA), CLINICAL TYPES OF SCHIZOPHRENIA, DIAGNOSIS, INVESTIGATION, TREATMENT MODALITIES(PHARMACOLOGICAL MANAGEMENT, PSYCHOTHERAPY, ECT, PSYCHO-SOCIO-REHABILITATION), NURSING MANAGEMENT(ASSESSMENT,DIAGNOSIS,NURSING INTERVENTION,AND EVALUATION), OTHER PSYCHOTIC DISORDER LIKE Persistent delusion/Capgras syndrome(The Delusion of Doubles)/Acute and Transient Psychotic Disorders/Induced Delusional Disorders/Schizoaffective Disorder /CAPGRAS SYNDROME(DELUSION OF DOUBLE), GERIATRIC CONSIDERATION, FOLLOW UP, HOMECARE AND REHABILITATION OF THE PATIENT, Filipino 9 Maikling Kwento Ang Ama Panitikang Asiyano
Filipino 9 Maikling Kwento Ang Ama Panitikang Asiyanosumadsadjelly121997
╠²
Filipino 9 Maikling Kwento Ang Ama Panitikang AsiyanoLAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...Ultimatewinner0342
╠²
ƒºá Lazy Sunday Quiz | General Knowledge Trivia by SMC Quiz Club ÔÇô Silchar Medical College
Presenting the Lazy Sunday Quiz, a fun and thought-provoking general knowledge quiz created by the SMC Quiz Club of Silchar Medical College & Hospital (SMCH). This quiz is designed for casual learners, quiz enthusiasts, and competitive teams looking for a diverse, engaging set of questions with clean visuals and smart clues.
ƒÄ» What is the Lazy Sunday Quiz?
The Lazy Sunday Quiz is a light-hearted yet intellectually rewarding quiz session held under the SMC Quiz Club banner. ItÔÇÖs a general quiz covering a mix of current affairs, pop culture, history, India, sports, medicine, science, and more.
Whether youÔÇÖre hosting a quiz event, preparing a session for students, or just looking for quality trivia to enjoy with friends, this PowerPoint deck is perfect for you.
ƒôï Quiz Format & Structure
Total Questions: ~50
Types: MCQs, one-liners, image-based, visual connects, lateral thinking
Rounds: Warm-up, Main Quiz, Visual Round, Connects (optional bonus)
Design: Simple, clear slides with answer explanations included
Tools Needed: Just a projector or screen ÔÇô ready to use!
ƒºá Who Is It For?
College quiz clubs
School or medical students
Teachers or faculty for classroom engagement
Event organizers needing quiz content
Quizzers preparing for competitions
Freelancers building quiz portfolios
ƒÆí Why Use This Quiz?
Ready-made, high-quality content
Curated with lateral thinking and storytelling in mind
Covers both academic and pop culture topics
Designed by a quizzer with real event experience
Usable in inter-college fests, informal quizzes, or Sunday brain workouts
ƒôÜ About the Creators
This quiz has been created by Rana Mayank Pratap, an MBBS student and quizmaster at SMC Quiz Club, Silchar Medical College. The club aims to promote a culture of curiosity and smart thinking through weekly and monthly quiz events.
ƒöì SEO Tags:
quiz, general knowledge quiz, trivia quiz, ║¦║¦▀úShare quiz, college quiz, fun quiz, medical college quiz, India quiz, pop culture quiz, visual quiz, MCQ quiz, connect quiz, science quiz, current affairs quiz, SMC Quiz Club, Silchar Medical College
ƒôú Reuse & Credit
YouÔÇÖre free to use or adapt this quiz for your own events or sessions with credit to:
SMC Quiz Club ÔÇô Silchar Medical College & Hospital
Curated by: Rana Mayank PratapJune 2025 Progress Update With Board Call_In process.pptx
June 2025 Progress Update With Board Call_In process.pptxInternational Society of Service Innovation Professionals
╠²
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...Ultimatewinner0342
╠²
Recurrence
- 1. RECURRENCE RELATION 1 Limits and Convergence For a sequence of real numbers x1, x2, x3, . . . , when n ÔêÆÔåÆ Ôê×, if xn ÔêÆÔåÆ s, then the sequence is said to be convergent (to s) and s is called the limit of the sequence. We write it as lim nÔåÆÔê× xn = s. Condition Variable Example Nil lim nÔåÆÔê× 1 n = 0 lim nÔåÆÔê× 1 3 + 2n = 0 0 Ôëñ a < 1 lim nÔåÆÔê× an = 0 lim nÔåÆÔê× 1 3 n = 0 b > 1 lim nÔåÆÔê× bn = Ôê× lim nÔåÆÔê× 3n = Ôê× Strictly increasing sequence A strictly increasing sequence is one where xn < xn+1, for all n Ôêê N. To show that a sequence is increasing, instead of showing xn < xn+1, it su´¼âces to show that xn ÔêÆ xn+1 < 0. Remark: When asked to describe the behaviour of a sequence we can (possibly) mention 2 things: 1. It is an increasing or decreasing sequence. 2. Is it convergent? If yes, what value does it converge to? If no, is it oscillating about 2 points? These can be checked using a GC. www.MathAcademy.sg 1 c 2014 Math Academy
- 2. Example 1 (2008/TJC/MYE(J1)/Q6). The numbers xn satisfy the relation xn+1 = 12 7ÔêÆxn for all positive integers n. It is given that as n ÔêÆÔåÆ Ôê×, xn ÔêÆÔåÆ s. (i) Find the exact value(s) of s. (ii) Show that if 3 < xn < 4, then xn+1 < xn. Solution: (i) xn+1 = 12 7 ÔêÆ xn As n ÔêÆÔåÆ Ôê×, xn, xn+1 ÔêÆÔåÆ s, therefore, s = 12 7 ÔêÆ s s(7 ÔêÆ s) = 12 ÔêÆs2 + 7s ÔêÆ 12 = 0 (s ÔêÆ 3)(s ÔêÆ 4) = 0 s = 3 or 4 (ii) Method 1: sketch y = xn+1 ÔêÆ xn We want to sketch y = xn+1 ÔêÆ xn = 12 7ÔêÆxn ÔêÆ xn. Replacing xn by x, we get y = 12 7ÔêÆx ÔêÆ x. 3 4 y = 12 7ÔêÆx ÔêÆ x x y From the graph, if 3 < xn < 4, then y < 0. y < 0 =ÔçÆ 12 7 ÔêÆ xn ÔêÆ xn < 0 =ÔçÆ xn+1 ÔêÆ xn < 0 =ÔçÆ xn+1 < xn. www.MathAcademy.sg 2 c 2014 Math Academy
- 3. Method 2: Sketch y = xn+1 and y = xn We want to sketch y = xn+1 = 12 7xn and y = xn. Replacing xn by x, we get y = 12 7x and y = x. y = x y = 12 7x 3 4 7 x y From the graph, if 3 < xn < 4, then, 12 7  xn < xn = xn+1 < xn. Method 3: Show algebraically xn+1  xn = 12 7  xn  xn = 12  xn(7  xn) 7  xn Since 3 < xn < 4, www.MathAcademy.sg 3 c 2014 Math Academy
- 4. Example 2 (2011/PJC/II/2 modi´¼üed). A sequence of positive real numbers x1, x2, x3, . . . satis´¼ües the recurrence relation xn+1 = ÔêÜ 3 + xn for n ÔëÑ 1. (a) If the ´¼ürst term x1 is 1.5, write down the 6th term, that is, x6, leaving your answer to 4 decimal places. (b) If the sequence converges to ╬▒, determine the exact value of ╬▒. [2] (c) By using a graphical method, prove that xn+1 > xn if 0 < x < ╬▒. [2] (d) Use a calculator to determine the behaviour of the sequence {xn} when x1 = 1. Hence state brie´¼éy how the results in (c) relate to the behaviour of the sequence. [2] Solution: (a) Using GC, x6 = 2.3009. (b) As n ÔêÆÔåÆ Ôê×, xn, xn+1 ÔêÆÔåÆ ╬▒, therefore, ╬▒ = ÔêÜ 3 + ╬▒ ╬▒2 = 3 + ╬▒ ╬▒2 ÔêÆ ╬▒ ÔêÆ 3 = 0 ╬▒ = 1 ┬▒ (ÔêÆ1)2 ÔêÆ 4(1)(ÔêÆ3) 2 = 1 ┬▒ ÔêÜ 13 2 ╬▒ = 1 + ÔêÜ 13 2 or 1 ÔêÆ ÔêÜ 13 2 (rej, since the sequence is positive) (c) We want to sketch y = xn+1 ÔêÆ xn = ÔêÜ 3 + xn ÔêÆ xn. Replacing xn by x, we get y = ÔêÜ 3 + x ÔêÆ x. 1+ ÔêÜ 13 2 y = ÔêÜ 3 + x ÔêÆ x x y From the graph, if 0 < xn < ╬▒, then y > 0. y > 0 =ÔçÆ ÔêÜ 3 + xn ÔêÆ xn > 0 =ÔçÆ xn+1 ÔêÆ xn > 0 =ÔçÆ xn+1 > xn. (d) Since 0 < x1 < ╬▒, by part (c), xn+1 > xn. Therefore the sequence is strictly increasing. Using GC, the sequence converges to 2.3028. www.MathAcademy.sg 4 c 2014 Math Academy
- 5. Example 3. A sequence of real numbers u1, u2, u3, . . . satis´¼ües the recurrence relation un+1 = 0.9un + 90, a Ôêê R for all positive integers n and u0 = 1000. Express un in terms n. Solution: un = 0.9unÔêÆ1 + 90 = 0.9[0.9unÔêÆ2 + 90] + 90 = 0.92 unÔêÆ2 + 0.9(90) + 90 = 0.92 [0.9unÔêÆ3 + 90] + 0.9(90) + 90 = 0.93 unÔêÆ3 + 0.92 (90) + 0.9(90) + 90 = ... = 0.9n u0 + 0.9nÔêÆ1 (90) + 0.9nÔêÆ2 (90) + ┬À ┬À ┬À + 90 = 0.9n u0 + 90(1 ÔêÆ 0.9n) 1 ÔêÆ 0.9 (GP: a = 90, r = 0.9, no. terms = n) = 0.9n u0 + 900(1 ÔêÆ 0.9n ) = 0.9n (u0 ÔêÆ 900) + 900 = 100(0.9n ) + 900 (Since u0 = 1000) www.MathAcademy.sg 5 c 2014 Math Academy
- 6. 2 Using GC A sequence of positive real numbers x1, x2, x3, . . . satis´¼ües the recurrence relation xn+1 = ÔêÜ 3 + xn for n ÔëÑ 1. If the ´¼ürst term x1 is 1.5, write down the 6th term, that is, x6, leaving your answer to 4 decimal places. REMEMBER: We must ´¼ürst convert the equation to un = ÔêÜ 3 + unÔêÆ1. Step What to do Screen 1 Press ÔÇÿMODEÔÇÖ button. Select ÔÇÿSEQÔÇÖ in the 4th row. 2 Press ÔÇÿY=ÔÇÖ button. Key in nMin = 1. (this means ur sequence starts from x1) Key in u(n) = 3 + u(n ÔêÆ 1). -Press ÔÇÿ2ndÔÇÖ, ÔÇÿ7ÔÇÖ for u. -Press ÔÇÿX,T, ╬©, nÔÇÖ for n. -unÔêÆ1 is keyed as u(n ÔêÆ 1). Key in u(nMin) = 1.5 (the value of u1) 3 Press ÔÇÿ2ndÔÇÖ, ÔÇÿGRAPHÔÇÖ to get the table. Scroll down to view more terms. www.MathAcademy.sg 6 c 2014 Math Academy
