Refleksi matematika
- 2. y P (x, y) A O yŌĆÖ X PŌĆÖ(xŌĆÖ, yŌĆÖ) Persamaan Transformasi Refleksi
- 3. Kelompok 3 : 1. 2. 3. 4. 5. 6. 7. 8. 9. Anas Rahman Deni Maulana Evan Valiant Gading Yoga Khusnul Khotimah M. Misbakhul Abid Nila Prameswari Rizal Medi F. Ni Luh Putu N. (07) (11) (23) (31) (03) (15) (19) (27) (35)
- 4. Refleksi Merupakan transformasi yang memindahkan titik-titik dengan menggunakan sifat bayangan oleh suatu cermin.
- 5. Persamaan Transformasi Refleksi pada Bidang 1. 2. 3. 4. 5. Persamaan Transformasi Refleksi Terhadap Sumbu X Persamaan Transformasi Refleksi Terhadap Sumbu Y Persamaan Transformasi Refleksi Terhadap Garis y =x Persamaan Transformasi Refleksi Terhadap Garis y = -x Persamaan Transformasi Refleksi Terhadap Titik
- 6. Persamaan Transformasi Refleksi Terhadap Sumbu X Y y xŌĆÖ = x yŌĆÖ = - y P (x, y) P(x, y) A O yŌĆÖ X PŌĆÖ(xŌĆÖ, yŌĆÖ) sumbu X PŌĆÖ (x, -y)
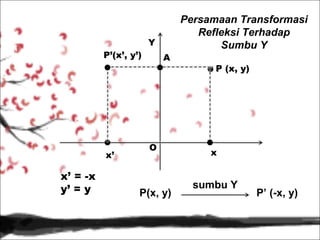
- 7. Y PŌĆÖ(xŌĆÖ, yŌĆÖ) xŌĆÖ xŌĆÖ = -x yŌĆÖ = y A O P(x, y) Persamaan Transformasi Refleksi Terhadap Sumbu Y P (x, y) x sumbu Y PŌĆÖ (-x, y)
- 8. A. Matriks Refleksi Terhadap Sumbu X Matriks refleksi terhadap sumbu X ditentukan dengan hubungan xŌĆÖ = x dan yŌĆÖ = -y adalah 1 0 0 -1 B. Matriks Refleksi Terhadap Sumbu Y Matriks refleksi terhadap sumbu Y ditentukan dengan hubungan xŌĆÖ = -x dan yŌĆÖ = y adalah -1 0 0 1
- 9. Y B Persamaan Transformasi Refleksi Terhadap Garis y = x P= (x, y) y=x PŌĆÖ = (xŌĆÖ, yŌĆÖ) O A X xŌĆÖ = y yŌĆÖ = x P(x, y) garis y = x PŌĆÖ (y, x)
- 10. Persamaan Transformasi Refleksi Terhadap Garis y = -x Y 3 -3 X 4 -4 P(x, y) xŌĆÖ = - y yŌĆÖ = - x garis y = -x PŌĆÖ (-y, -x)
- 11. C. Matriks Refleksi Terhadap Garis y = x Matriks refleksi terhadap garis y = x ditentukan dengan hubungan xŌĆÖ = y dan yŌĆÖ = x adalah 0 1 1 0 D. Matriks Refleksi Terhadap Garis y = -x Matriks refleksi terhadap garis y = - x ditentukan dengan hubungan xŌĆÖ = -y dan yŌĆÖ = -x adalah 0 -1 -1 0
- 12. Persamaan Transformasi Refleksi Terhadap Titik Asal O (0, 0) Y B P (x, y) A O X P (x, y) PŌĆÖ (xŌĆÖ, yŌĆÖ) xŌĆÖ = -x yŌĆÖ = -y titik asal O PŌĆÖ (-x, -y)
- 13. E. Matriks Refleksi Terhadap Titik Asal O (0, 0) Matriks refleksi terhadap titik asal O (0, 0) ditentukan dengan hubungan xŌĆÖ = -x dan yŌĆÖ = -y adalah -1 0 0 -1
- 14. Persamaan Transformasi Refleksi Terhadap Garis x = h Y O P (x, y) A x=h PŌĆÖ (xŌĆÖ, yŌĆÖ) B xŌĆÖ = 2h ŌĆō x yŌĆÖ = y P (x, y) x=h C X ’āś OA = x dan OB = h, sehingga AB = h ŌĆō x BC = AB = h ŌĆō x OC = OB + BC Ōćö xŌĆÖ = h + h ŌĆō x Ōćö xŌĆÖ = 2h ŌĆō x ’āś CPŌĆÖ = AP yŌĆÖ = y PŌĆÖ (2h - x, y)
- 15. Persamaan Transformasi Refleksi Terhadap Garis y = k Y C PŌĆÖ = (xŌĆÖ, yŌĆÖ) y=k B A O ’āś CPŌĆÖ = AP xŌĆÖ = x ’āś OA = y dan OB = k, maka AB = OB ŌĆō OA = k - y BC = AB = k ŌĆō y OC = OB + BC Ōćö yŌĆÖ = k + (k ŌĆō y) Ōćö yŌĆÖ = 2k - y xŌĆÖ = x yŌĆÖ = 2k - y P = (x, y) X P (x, y) y=k PŌĆÖ (x, 2k -y)
- 17. Komposisi Refleksi 1. 2. 3. Terhadap refleksi tegak lurus Saling berpotongan di titik 0,0 Sejajar sumbu x dan sumbu y
- 18. y A = (-1,4) Tegak Lurus AŌĆÖ = (1,4) x AŌĆØ = (1,-4)
- 19. ’é× Refleksi terhadap dua sumbu saling tegak lurus Jika titik A(x,y) direfleksikan terhadap garis x=a dilanjutkan terhadap garis y=b (dua sumbu yang saling tegak lurus) maka bayangan akhir A adalah sama dengan rotasi titik A(x,y) dengan pusat titik potong dua sumbu (garis) dan sudut putar 180╦Ü
- 20. Y Refleksi terhadap dua sumbu yang saling berpotongan Jika titik A(x,y) direleksikan terhadap garis g dilanjutkan terhadap garis h, maka bayangan akhirnya adalah dengan pusat perpotongan garis g dan h dan sudut putar 2╬▒(╬▒ sudut antara garis g dan h) serta arah putaran dari garis g ke h. ╬▓ ╬Ė ╬▓ ╬▒ ╬▒ X
- 21. Sejajar sumbu x AŌĆØ AŌĆÖ A Komposisi dua refleksi berurutan refleksi berurutan terhadap dua sumbu sejajar dengan sumbu x Jika titik A(x,y) direfleksikan terhadap garis y=a dilanjutkan terhadap garis y=b. Maka bayangan akhir A adalah yaitu: xŌĆśŌĆÖ=x yŌĆśŌĆÖ=2(b-a)+y
- 22. Sejajar sumbu y Jika titik A(x,y) direfleksikan terhadap garis x=a dilanjutkan terhadap garis x=b. Maka bayangan akhir A adalah yaitu: x'=2(b-a)+x y'=y Y A AŌĆÖ AŌĆØ X
- 23. Sif at Komposisi Ref leksi ’é× Komposisi refleksi (refleksi berurutan) pada umumnya tidak komutatif kecuali komposisi refleksi terhadap sumbu x dilanjutkan terhadap sumbu y (dua sumbu yang saling tegak lurus). ┬Ā
- 24. Contoh Soal 1. Tentukan koordinat bayangan titik P(4,2) oleh refleksi terhadap sumbu x dilanjutkan dengan refleksi terhadap sumbu y Jawab: P(4,2) direfleksikan terhadap sumbu x P(4,2) PŌĆÖ(4 , -2) Titik PŌĆÖ(4,-2) direfleksikan terhadap sumbu y PŌĆÖ(4,-2) PŌĆØ(-4,-2) Jadi koordinat bayangan titikP(4,2) oleh refleksi terhadap sumbu x dilanjutkan Dengan refleksi terhadap sumbu y adalah PŌĆØ(-4,-2) dan dapat ditulis: Y o X (4,2) = ( -4, -2 ).
- 25. 2. Tentukan koor dinat bayangan titik P(4,2) oleh r efleksi ter hadap sumbu x dilanjutkan dengan r efleksi ter hadap sumbu y Jawab: P(4,2) dir efleksikan ter hadap sumbu x P(4,2) PŌĆÖ(4 , -2) Titik PŌĆÖ(4,-2) dir efleksikan ter hadap sumbu y PŌĆÖ(4,-2) PŌĆØ(-4,-2) Jadi koor dinat bayangan titikP(4,2) oleh r efleksi ter hadap sumbu x dilanjutkan Dengan r efleksi ter hadap sumbu y adalah PŌĆØ(-4,-2) dan dapat ditulis: Y o X (4,2) = ( -4, -2 ).