repaso sobre logica
- 1. 1.- P Q ( ╠┤ P ╩ī Q ) ŌåÆ ( ╠┤ ( ╠┤ P ╩ī Q ) ╦ģ R ) V V F F V V V F F V V V V V F F V V V F F V V F V F F F F V V F F F V V V F F F F V V F F F V F F V V V V V F V V V V V F V V V V F F V V V F F F F V F F V V V F F V V F F V F F V V V F F V F 2.- P Q ((P ╦ģ Q ) ŌåÉ R ) Ōåö (( ╠┤ P ╩ī Q ) ŌåÆ S ) V V V V V V V V F F V V V V V V V V V V V F F V V F V V V V V V F V F F V V V V V V V V V F V F F V V F V F V V F V V V F F F V V V F V V F V V V F F F V F V F V V F V F V F F F V V V F V V F V F V F F F V F F V F V V V V V V V V V V F V F V V V V F V V V F F F V F V V V F V V V V V V F V F V V V F F V V V F F F F F F F F V F V F F V V F F F F F F V F V F F V F F F F F F V F V V F F V V F F F F F V F V V F F V F
- 2. 3.- P Q [ ( ╠┤ ( Q ╩ī T ) ╦ģ ( R ╦ģ P ) ) ŌåÆ Q ╩ī ( ╠┤ T Ōåö S ) ] V V F V V V V V V V F V F F F V V V V V F F V V V V V V V V V V V V F V V V V V V V V V V F V F V V V V F F V V V V F V F V F F V V F V V V V F V V F V F F F V V V V V F F V F V V V V V V V V V V F V V V V F V V V V V F V F V V V V F F V F V V F V F V F F V F V F F V V V V V F F F F F V V F V F F F V V V V F F F V V V V F V F F V V V V V F F F F V F V F V F F F V V V V F F F V F F V F V F F V V F V V F F F F F V V F V F F F V F V V F F F V V V V F V F F V V F V V F F F F V F V F V F F F V F V V F F F V F F F V F V V V V V V F F V F F F V F V V V F F V V V F V V V V V V F V F V V V V V V F V V V F V F F V V V F F V V V F F V F V F F F V F V V V F F F F V V F F F V F V V V F F V F F F V V V V V V F V F V V V F F F F V V V F V F F V V V F F V F F F F V F V F F F F V F F V V V V F F F F F F V F F V F F F V V V F F F F V V V F F V F F V V V V F F F F F V F F F V F F F V V V F F F F V F F F F V F F V V F F F F F F F F V F F V F F F V F F F F F F V V V F F V F F V V F F F F F F F V F F F V F F F V F F F F F F V F F
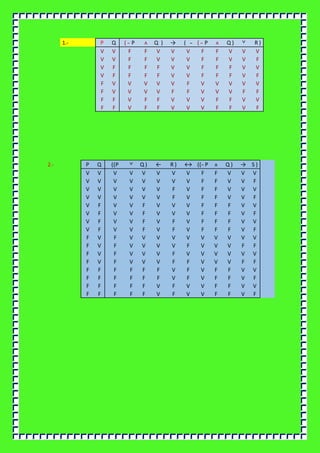
![3.- P Q [ ( ╠┤ ( Q ╩ī T ) ╦ģ ( R ╦ģ P ) ) ŌåÆ Q ╩ī ( ╠┤ T Ōåö S ) ]
V V F V V V V V V V F V F F F V
V V V V F F V V V V V V V V V V
V V F V V V V V V V V V V F V F
V V V V F F V V V V F V F V F F
V V F V V V V F V V F V F F F V
V V V V F F V F V V V V V V V V
V V F V V V V F V V V V V F V F
V V V V F F V F V V F V F V F F
V F V F F V V V V V F F F F F V
V F V F F F V V V V F F F V V V
V F V F F V V V V V F F F F V F
V F V F F F V V V V F F F V F F
V F V F F V V F V V F F F F F V
V F V F F F V F V V F F F V V V
V F V F F V V F V V F F F F V F
V F V F F F V F V V F F F V F F
F V F V V V V V V F F V F F F V
F V V V F F V V V F V V V V V V
F V F V V V V V V F V V V F V F
F V V V F F V V V F F V F V F F
F V F V V V F F F F V V F F F V
F V V V F F V F F F V V V V V V
F V F V V V F F F F V V V F V F
F V V V F F V F F F F V F V F F
F F V F F V V V V F F F F F F V
F F V F F F V V V F F F F V V V
F F V F F V V V V F F F F F V F
F F V F F F V V V F F F F V F F
F F V F F V V F F F F F F F F V
F F V F F F V F F F F F F V V V
F F V F F V V F F F F F F F V F
F F V F F F V F F F F F F V F F](https://image.slidesharecdn.com/1-161025013519/85/repaso-sobre-logica-2-320.jpg)