Rt de syd
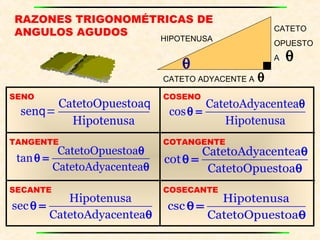
- 4. RAZONES TRIGONOM?TRICAS DE
ANGULOS AGUDOS
q
=q
CatetoOpuestoa
sen
Hipotenusa
¦È
¦È =
CatetoAdyacentea
cos
Hipotenusa
¦È =
¦È
Hipotenusa
sec
CatetoAdyacentea
¦È =
¦È
Hipotenusa
csc
CatetoOpuestoa
¦È
¦È =
¦È
CatetoAdyacentea
cot
CatetoOpuestoa
¦È
¦È =
¦È
CatetoOpuestoa
tan
CatetoAdyacentea
CATETO
OPUESTO
A
¦ÈCATETO ADYACENTE A
¦È
HIPOTENUSA
¦È
SENO COSENO
TANGENTE COTANGENTE
SECANTE COSECANTE
- 5. 12
35
H
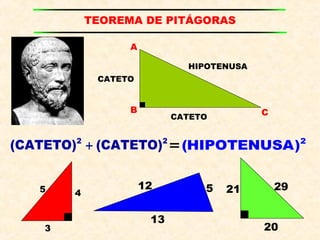
2 2 2
H 12 35= +
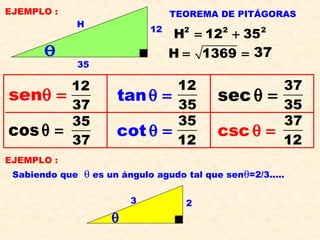
TEOREMA DE PIT?GORAS
H 1369= = 37
sen¦È =
cos¦È =
tan¦È =
12
37
35
37
12
35
cot ¦È =
sec ¦È =
csc ¦È =
35
12
37
35
37
12
EJEMPLO :
EJEMPLO :
Sabiendo que ¦È es un ¨¢ngulo agudo tal que sen¦È=2/3.....
23
¦È
¦È
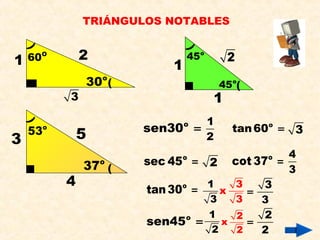
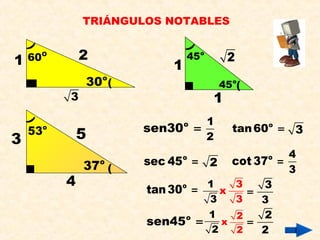
- 6. TRI?NGULOS NOTABLES
1 2
3
o
30 (
)
O
60
1
1
2
o
45
o
45
(
)
3
4
5
o
37
o
53
(
)
o
sen30 =
1
2
o
tan60 = 3
o
sec 45 = 2
o
cot 37 =
4
3
o
tan30 =
1
3
3
x
3
3
3
=
o
sen45 =
1
2
2
x
2
2
2
=
- 7. TRI?NGULOS NOTABLES
1 2
3
o
30 (
)
O
60
1
1
2
o
45
o
45
(
)
3
4
5
o
37
o
53
(
)
o
sen30 =
1
2
o
tan60 = 3
o
sec 45 = 2
o
cot 37 =
4
3
o
tan30 =
1
3
3
x
3
3
3
=
o
sen45 =
1
2
2
x
2
2
2
=