SAE 2007-NVC-180
- 1. 1 SAE Noise and Vibration Conference May 15-17, 2007 A Simple Model for the Simulation ofA Simple Model for the Simulation of Low-Frequency Disc Brake NoiseLow-Frequency Disc Brake Noise Ragnar Ledesma and Shan ShihRagnar Ledesma and Shan Shih Advanced EngineeringAdvanced Engineering Commercial Vehicle SystemsCommercial Vehicle Systems
- 2. 2 SAE Noise and Vibration Conference May 15-17, 2007 ObjectiveObjective âĒ The objective of this study is to develop a simple multi- body dynamics model that can simulate low-frequency disc brake noise âĒ Verify the hypothesis that low-frequency brake noise can be caused by the coupling of 2 vibration modes through a friction interface âĒ A second objective is to determine the effect of various design parameters on brake noise propensity âĒ brake pad/brake rotor sliding friction coefficient âĒ brake pad stiffness (pad compressibility) âĒ bushing stiffness (suspension lateral stiffness)
- 3. 3 SAE Noise and Vibration Conference May 15-17, 2007 Modeling AssumptionsModeling Assumptions âĒ Brake noise is a manifestation of friction-induced mode coupling âĒ The friction interface is characterized by 2 parameters: normal contact stiffness and sliding friction coefficient âĒ Mode coupling is an instability phenomenon that occurs when e nn kF Îī*= e nf kF ÎīÂĩ **= )2/()2sin( nkKâ>Îģ ÂĩÎģ =)tan(
- 4. 4 SAE Noise and Vibration Conference May 15-17, 2007 Multi-Body Dynamics ModelMulti-Body Dynamics Model âĒ Disc brake assembly âĒ Torque plate (flexible â use FE model) âĒ Caliper (rigid) âĒ Rotor and brake pads (rigid) âĒ Push rods/pistons (rigid) âĒ Pad/Rotor normal contact â Hertz contact model âĒ Friction model: constant sliding friction coefficient âĒ Typical suspension system for heavy-duty bus/coach âĒ Upper and lower torque rods âĒ Air springs/shock absorbers âĒ Beam axle âĒ Truck tires
- 5. 5 SAE Noise and Vibration Conference May 15-17, 2007 ADAMS Model (Disc Brake Assembly)ADAMS Model (Disc Brake Assembly)
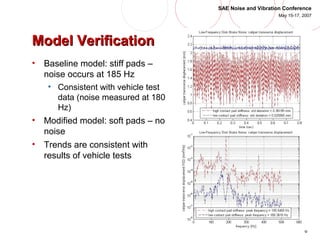
- 6. 6 SAE Noise and Vibration Conference May 15-17, 2007 Model VerificationModel Verification âĒ Baseline model: stiff pads â noise occurs at 185 Hz âĒ Consistent with vehicle test data (noise measured at 180 Hz) âĒ Modified model: soft pads â no noise âĒ Trends are consistent with results of vehicle tests
- 7. 7 SAE Noise and Vibration Conference May 15-17, 2007 Designed Numerical ExperimentsDesigned Numerical Experiments âĒ Determine the effect of design parameters on the propensity of low-frequency disc brake noise âĒ 3-factor, 3-level design (27 runs) Design Factor Assigned Values A. Coefficient of Friction (0.2, 0.3, 0.4) B. Pad Stiffness (1.0, 5.5, 10.0) x 105 N/mm C. Bushing Stiffness (1.0, 5.5, 10.0) x 104 N/mm
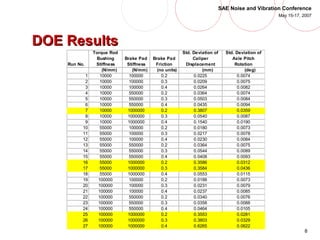
- 8. 8 SAE Noise and Vibration Conference May 15-17, 2007 DOE ResultsDOE Results Run No. Torque Rod Bushing Stiffness Brake Pad Stiffness Brake Pad Friction Std. Deviation of Caliper Displacement Std. Deviation of Axle Pitch Rotation (N/mm) (N/mm) (no units) (mm) (deg) 1 10000 100000 0.2 0.0225 0.0074 2 10000 100000 0.3 0.0209 0.0075 3 10000 100000 0.4 0.0264 0.0082 4 10000 550000 0.2 0.0364 0.0074 5 10000 550000 0.3 0.0503 0.0084 6 10000 550000 0.4 0.0435 0.0094 7 10000 1000000 0.2 0.3807 0.0359 8 10000 1000000 0.3 0.0540 0.0087 9 10000 1000000 0.4 0.1540 0.0190 10 55000 100000 0.2 0.0180 0.0073 11 55000 100000 0.3 0.0217 0.0078 12 55000 100000 0.4 0.0230 0.0084 13 55000 550000 0.2 0.0364 0.0075 14 55000 550000 0.3 0.0544 0.0089 15 55000 550000 0.4 0.0408 0.0093 16 55000 1000000 0.2 0.3586 0.0312 17 55000 1000000 0.3 0.3584 0.0436 18 55000 1000000 0.4 0.0553 0.0115 19 100000 100000 0.2 0.0188 0.0073 20 100000 100000 0.3 0.0231 0.0079 21 100000 100000 0.4 0.0237 0.0085 22 100000 550000 0.2 0.0340 0.0076 23 100000 550000 0.3 0.0358 0.0088 24 100000 550000 0.4 0.0464 0.0105 25 100000 1000000 0.2 0.3553 0.0281 26 100000 1000000 0.3 0.3803 0.0329 27 100000 1000000 0.4 0.6265 0.0622
- 9. 9 SAE Noise and Vibration Conference May 15-17, 2007 ANOVA Table: Inverse of the VibrationANOVA Table: Inverse of the Vibration Amplitude of the Caliper (Side-to-Side Mode)Amplitude of the Caliper (Side-to-Side Mode) Sum of Mean F Source Squares DF Square Value Prob > F Model 7347.51 6 1224.59 54.70 < 0.0001 A - Friction Coeff 41.13 1 41.13 1.84 0.1904 B - Pad Stiffness 7030.79 1 7030.79 314.07 < 0.0001 C - Bushing Stiffness 0.74 1 0.74 0.03 0.8577 A*B 189.91 1 189.91 8.48 0.0086 A*C 14.33 1 14.33 0.64 0.4330 B*C 70.60 1 70.60 3.15 0.0910 Residual 447.73 20 22.39 Cor Total 7795.24 26 Std. Dev. 4.73 R-Squared 0.94 Mean 25.63 Adj R-Squared 0.93 C.V. 18.46 Pred R-Squared 0.90
- 10. 10 SAE Noise and Vibration Conference May 15-17, 2007 Predicted Response: Inverse of the VibrationPredicted Response: Inverse of the Vibration Amplitude of the Caliper (Side-to-Side Mode)Amplitude of the Caliper (Side-to-Side Mode) 3.40172 15.2726 27.1435 39.0143 50.8852 1.0/(Std.Dev.-CaliperDisp.) 0.20 0.25 0.30 0.35 0.40 100000.00 325000.00 550000.00 775000.00 1000000.00 A: Friction C oefficient B: Pad Stiffness
- 11. 11 SAE Noise and Vibration Conference May 15-17, 2007 ANOVA Table: Inverse Squared of the AxleANOVA Table: Inverse Squared of the Axle Pitch Rotation (Spring Wrap-Up Mode)Pitch Rotation (Spring Wrap-Up Mode) Sum of Mean F Source Squares DF Square Value Prob > F Model 7.37E+09 5 1.47E+09 25.85 < 0.0001 A - Friction Coeff. 3.69E+08 1 3.69E+08 6.47 0.0189 B - Pad Stiffness 5.88E+09 1 5.88E+09 103.09 < 0.0001 C - Bushing Stiffness 1.76E+08 1 1.76E+08 3.09 0.0934 B*B 6.87E+08 1 6.87E+08 12.03 0.0023 A*B 2.60E+08 1 2.60E+08 4.56 0.0447 Residual 1.20E+09 21 5.71E+07 Cor Total 8.57E+09 26 Std. Dev. 7553.80 R-Squared 0.86 Mean 29161.60 Adj R-Squared 0.83 C.V. 25.90 Pred R-Squared 0.77
- 12. 12 SAE Noise and Vibration Conference May 15-17, 2007 Predicted Response: Inverse Squared of thePredicted Response: Inverse Squared of the Axle Pitch Rotation (Spring Wrap-Up Mode)Axle Pitch Rotation (Spring Wrap-Up Mode) 7388.71 18755.9 30123 41490.1 52857.3 (Std.Dev.-AxleWrap-Up)^-2.2 0.20 0.25 0.30 0.35 0.40 100000.00 325000.00 550000.00 775000.00 1000000.00 A: Friction C oefficient B: Pad Stiffness
- 13. 13 SAE Noise and Vibration Conference May 15-17, 2007 Sample Results: Effect of Friction on BrakeSample Results: Effect of Friction on Brake Noise FrequencyNoise Frequency Time History Frequency Spectrum
- 14. 14 SAE Noise and Vibration Conference May 15-17, 2007 ConclusionConclusion âĒ A simple multi-body dynamics model was developed to simulate low-frequency disc brake noise âĒ The assumed mechanism for noise generation is the friction-induced mode coupling (axle wrap-up mode and caliper transverse mode) âĒ Rigid body models (with a few flexible components) are sufficient to simulate the low-frequency noise âĒ Designed numerical experiments show that the primary design parameter is the brake pad stiffness âĒ Modeling of brake squeal will require FE model of brake rotor in order to capture nodal diameter modes