Sampling theorem
•Download as PPT, PDF•
0 likes•311 views
The document discusses periodic sampling of continuous-time signals to create discrete-time signals. It explains that when sampling a continuous-time signal x(t) at intervals of T seconds, the discrete-time signal x(n) equals x(nT). It also states that for the discrete-time signal x(n) to uniquely represent the original continuous-time signal x(t), the sampling frequency must be greater than twice the maximum frequency of x(t), which is known as the Nyquist rate.
Sampling theorem
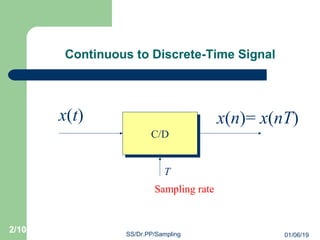
- 2. Continuous to Discrete-Time Signal C/DC/D T x(t) x(n)= x(nT) Sampling rate 01/06/19 2/10 SS/Dr.PP/Sampling
- 3. Continuous to Discrete-Time Signal Conversion from impulse train to discrete-time sequence Conversion from impulse train to discrete-time sequence x(t) x(nT) × s(t) xs(t) 01/06/19 3/10 SS/Dr.PP/Sampling
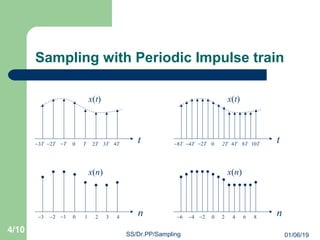
- 4. Sampling with Periodic Impulse train t x(t) 0 T 2T 3T 4T−T−2T−3T n x(n) 0 1 2 3 4−1−2−3 t x(t) 0 2T 4T 8T 10T−2T−4T−8T n x(n) 0 2 4 6 8−2−4−6 01/06/19 4/10 SS/Dr.PP/Sampling
- 5. Sampling with Periodic Impulse train t x(t) 0 T 2T 3T 4T−T−2T−3T n x(n) 0 1 2 3 4−1−2−3 t x(t) 0 2T 4T 8T 10T−2T−4T−8T n x(n) 0 2 4 6 8−2−4−6 What condition has to be placed on the sampling rate? What condition has to be placed on the sampling rate? We want to restore x(t) from x(n).We want to restore x(t) from x(n). 01/06/19 5/10 SS/Dr.PP/Sampling
- 6. Continuous to Discrete-Time Signal Conversion from impulse train to discrete-time sequence Conversion from impulse train to discrete-time sequence x (t) x(nT) × s(t) xs(t) ∑ ∞= −∞= −δ= n n nTtts )()( )()()( tstxtxs = ∑ ∞= −∞= −= n n nTttx )()( δ ∑ ∞= −∞= −= n n nTtnTx )()( δ 01/06/19 6/10 SS/Dr.PP/Sampling
- 7. Continuous to Discrete-Time Signal Conversion from impulse train to discrete-time sequence Conversion from impulse train to discrete-time sequence xc(t) x(n)= x(nT) × s(t) xs(t) ∑ ∞= −∞= −δ= n n nTtts )()( )()()( tstxtxs = ∑ ∞= −∞= −= n n nTttx )()( δ ∑ ∞= −∞= −= n n nTtnTx )()( δ )(*)( 2 1 )( ωω π ω jSjXjXs = T k T jS s k s π ωωωδ π ω 2 ,)( 2 )( =−= ∑ ∞ −∞= 01/06/19 7/10 SS/Dr.PP/Sampling
- 8. Continuous to Discrete-Time Signal )(*)( 2 1 )( ωω Ï€ ω jSjXjXs = T k T jS s k s Ï€ ωωωδ Ï€ ω 2 ,)( 2 )( =−= ∑ ∞ −∞= ωs: Sampling Frequency     ï£ ï£« −= ∑ ∞ −∞=k ss k T jXjX )( 2 *)( 2 1 )( ωωδ Ï€ ω Ï€ ω 01/06/19 8/10 SS/Dr.PP/Sampling
- 9. Continuous to Discrete-Time Signal     ï£ ï£« −= ∑ ∞ −∞=k ss k T jXjX )( 2 *)( 2 1 )( ωωδ Ï€ ω Ï€ ω ∑ ∞ −∞= −= k skjX T )(*)( 1 ωωδω ∑ ∞ −∞= −= k skjX T ))(( 1 ωω ∑ ∞ −∞= −= k ss kjX T jX ))(( 1 )( ωωω Therefore Xs(jω) is a periodic function of ω, consisting of a superposition of shifted replicas of X(jω), scaled by 1/T. 01/06/19 9/10 SS/Dr.PP/Sampling
- 10. Sampling Theroem Let x(t) be a band (frequency)-limited signal X(jω) = 0 for |ω|>ωM. Then x(t) is uniquely determined by its samples {x(nT)} when the sampling frequency satisfies: where ωs=2π/T. 2ωM is known as the Nyquist rate, as it represents the largest frequency that can be reproduced with the sample time 01/06/1910/10 SS/Dr.PP/Sampling